(鲁教版)2022-2023学年度第一学期八年级数学4.2图形的旋转 同步测试
试卷更新日期:2022-10-26 类型:同步测试
一、单选题
-
1. 将△OBA按如图方式放在平面直角坐标系中,其中∠OBA=90°,∠A=30°,顶点A的坐标为 , 将△OAB绕原点逆时针旋转,每次旋转60°,则第2023次旋转结束时,点A对应点的坐标为( )
 A、 B、 C、 D、2. 如图,在等腰直角中, , D为内一点,将线段绕点C逆时针旋转90°后得到 , 连接 , 若 , 则是( )
A、 B、 C、 D、2. 如图,在等腰直角中, , D为内一点,将线段绕点C逆时针旋转90°后得到 , 连接 , 若 , 则是( ) A、75° B、78° C、80° D、92°3. 如图,在中, , 将绕点A按顺时针方向旋转得到 . 若点恰好落在边上,且 , 则的度数为( )
A、75° B、78° C、80° D、92°3. 如图,在中, , 将绕点A按顺时针方向旋转得到 . 若点恰好落在边上,且 , 则的度数为( ) A、 B、 C、 D、4. 如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知BC=4,则E′D′=( )
A、 B、 C、 D、4. 如图,△ABC以点O为旋转中心,旋转180°后得到△A′B′C′.ED是△ABC的中位线,经旋转后为线段E′D′.已知BC=4,则E′D′=( )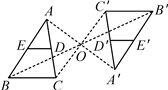 A、2 B、3 C、4 D、1.55. 如图,在△ABC中,∠CAB=66°.在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'的度数为( )
A、2 B、3 C、4 D、1.55. 如图,在△ABC中,∠CAB=66°.在同一平面内,将△ABC绕点A旋转到△AB'C'的位置,使得CC'∥AB,则∠BAB'的度数为( ) A、70° B、50° C、40° D、48°6. 如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,若点A的坐标为(-4,-3),则点A′的坐标为( )
A、70° B、50° C、40° D、48°6. 如图,将△ABC绕点C(0,-1)旋转180°得到△A′B′C,若点A的坐标为(-4,-3),则点A′的坐标为( ) A、 B、 C、 D、7. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )
A、 B、 C、 D、7. 如图,在Rt△ABC中,∠ACB=90°,∠A=60°,AC=6,将△ABC绕点C按逆时针方向旋转得到△A'B'C',此时点A'恰好在AB边上,则点B'与点B之间的距离为( )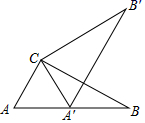 A、12 B、6 C、6 D、8. 在平面直角坐标系中,已知点A(3,﹣3),在坐标轴上确定一点B,使△AOB为等腰三角形,则符合条件的点B共有( )个A、5 B、6 C、7 D、89. 对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(2,0),点Q是直线l上的一点,点A关于点Q的对称点为点B,点B关于直线l的对称点为点C,若点B由点A经n次斜平移后得到,且点C的坐标为(8,6),则△ABC的面积是( )
A、12 B、6 C、6 D、8. 在平面直角坐标系中,已知点A(3,﹣3),在坐标轴上确定一点B,使△AOB为等腰三角形,则符合条件的点B共有( )个A、5 B、6 C、7 D、89. 对于坐标平面内的点,先将该点向右平移1个单位,再向上平移2个单位,这种点的运动称为点的斜平移,如点P(2,3)经1次斜平移后的点的坐标为(3,5).已知点A的坐标为(2,0),点Q是直线l上的一点,点A关于点Q的对称点为点B,点B关于直线l的对称点为点C,若点B由点A经n次斜平移后得到,且点C的坐标为(8,6),则△ABC的面积是( )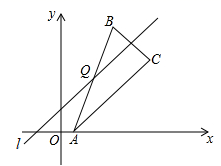 A、12 B、14 C、16 D、1810. 全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图1),若运动方向相反,则称它们是镜面合同三角形(如图2),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°,下列各组合同三角形中,是镜面合同三角形的是( )
A、12 B、14 C、16 D、1810. 全等三角形又叫做合同三角形,平面内的合同三角形分为真正合同三角形与镜面合同三角形,假设△ABC和△A1B1C1是全等(合同)三角形,点A与点A1对应,点B与点B1对应,点C与点C1对应,当沿周界A→B→C→A,及A1→B1→C1→A1环绕时,若运动方向相同,则称它们是真正合同三角形(如图1),若运动方向相反,则称它们是镜面合同三角形(如图2),两个真正合同三角形都可以在平面内通过平移或旋转使它们重合,两个镜面合同三角形要重合,则必须将其中一个翻转180°,下列各组合同三角形中,是镜面合同三角形的是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 如图,在Rt△ABC中,C为直角顶点,∠ABC=20°,O为斜边的中点,将OA绕着点O逆时针旋转θ°(0<θ<180)至OP,当△BCP恰为轴对称图形时,θ的值为 .
 12. 如图,在平面直角坐标系xOy中,三角板的直角顶点P的坐标为(2,2),一条直角边与x轴的正半轴交于点A,另一直角边与y轴交于点B,三角板绕点P在坐标平面内转动的过程中,当△POA为等腰三角形时,请写出所有满足条件的点B的坐标 .
12. 如图,在平面直角坐标系xOy中,三角板的直角顶点P的坐标为(2,2),一条直角边与x轴的正半轴交于点A,另一直角边与y轴交于点B,三角板绕点P在坐标平面内转动的过程中,当△POA为等腰三角形时,请写出所有满足条件的点B的坐标 .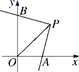 13. 如图,P是正方形ABCD内一点,将绕点B顺时针方向旋转,能与重合,若 , 则 .
13. 如图,P是正方形ABCD内一点,将绕点B顺时针方向旋转,能与重合,若 , 则 . 14. 如图,将n个边长都为1的正方形按如图所示摆放,点A1 , A2 , …,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为 .
14. 如图,将n个边长都为1的正方形按如图所示摆放,点A1 , A2 , …,An分别是正方形的中心,则n个正方形重叠形成的重叠部分的面积和为 .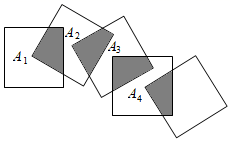 15. 如图,P为等边△ABC的边BC上任一点,点D在BA的延长线上,将线段PD绕点P逆时针旋转60°得线段PE,连BE,则∠CBE=.
15. 如图,P为等边△ABC的边BC上任一点,点D在BA的延长线上,将线段PD绕点P逆时针旋转60°得线段PE,连BE,则∠CBE=.
三、解答题
-
16. 如图,点 是等边△ 内一点, , , .求 的度数.
 17. 如图所示,已知 为正方形 外的一点. , .将 绕点 顺时针旋转 ,使点 旋转至点 ,且 ,求 的度数.
17. 如图所示,已知 为正方形 外的一点. , .将 绕点 顺时针旋转 ,使点 旋转至点 ,且 ,求 的度数. 18. 如图,将 绕直角顶点 按逆时针方向旋转 得到 .已知 ,求 的度数.
18. 如图,将 绕直角顶点 按逆时针方向旋转 得到 .已知 ,求 的度数. 19. 如图,在等边 中, ,点 在 上,且 ,点E是 上一动点,连接 ,将线段 绕点D逆时针旋转 ,得到线段 ,要使点F恰好落在 上,则 的长是多少?
19. 如图,在等边 中, ,点 在 上,且 ,点E是 上一动点,连接 ,将线段 绕点D逆时针旋转 ,得到线段 ,要使点F恰好落在 上,则 的长是多少?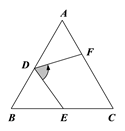 20. 如图,在平面直角坐标系中,已知 是等边三角形,点 的坐标是 ,点 在第一象限, 的平分线交 轴于点 ,把 绕着点 按逆时针方向旋转,使边 与 重合,得到 ,连接 .求: 的长及点 的坐标.
20. 如图,在平面直角坐标系中,已知 是等边三角形,点 的坐标是 ,点 在第一象限, 的平分线交 轴于点 ,把 绕着点 按逆时针方向旋转,使边 与 重合,得到 ,连接 .求: 的长及点 的坐标. 21. 如图,E点是正方形ABCD中CD边上任意一点,EF⊥AE于E点并交BC边于F点,以点A为中心,把△ADE顺时针旋转90°得到△ABE′.试说明:EE′平分∠AEF.
21. 如图,E点是正方形ABCD中CD边上任意一点,EF⊥AE于E点并交BC边于F点,以点A为中心,把△ADE顺时针旋转90°得到△ABE′.试说明:EE′平分∠AEF. 22. 如图,在由边长为1的小正方形组成的方格纸中,有两个全等的三角形,即△A1B1C1和△A2B2C2 . 请你指出在方格纸内如何运用平移、旋转变换,将△A1B1C1重合到△A2B2C2上.
22. 如图,在由边长为1的小正方形组成的方格纸中,有两个全等的三角形,即△A1B1C1和△A2B2C2 . 请你指出在方格纸内如何运用平移、旋转变换,将△A1B1C1重合到△A2B2C2上. 23. 阅读下列材料:
23. 阅读下列材料:【材料】如图,对任意符合条件的直角三角形BAC,绕其锐角顶点逆时针旋转90°得△DAE,所以∠BAE=90°,且四边形ACFD是一个正方形,它的面积和四边形ABFE面积相等,而四边形ABFE面积等于Rt△BAE和Rt△BFE的面积之和,根据图形我们就能证明勾股定理: .
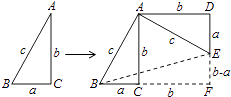

【请回答】如图是任意符合条件的两个全等的Rt△BEA和Rt△ACD拼成的,你能根据图示再写一种证明勾股定理的方法吗?