（鲁教版）2022-2023学年度第一学期七年级数学6.5一次函数的应用 同步测试
试卷更新日期：2022-10-26 类型：同步测试
一、单选题
-
1. 在同一平面直角坐标系中，直线y=2x+3与直线y=-5x+b的交点不可能在（ ）A、第一象限 B、第二象限 C、第三象限 D、第四象限2. 已知A，B两地相距3千米，小黄从A地到B地，平均速度为4千米/时，若用x表示行走的时间(小时)，y表示余下的路程(千米)，则y关于x的函数解析式是（ ）A、y=4x(x≥0) B、y=4x-8(x≥ ) C、y=3-4x(x≥0) D、y=3-4z(0≤x≤ )3. 若直线l1经过点(0，4)，l2经过点(3，2)，且l1与l2关于x轴对称，则l1与l2的交点坐标为（ ）A、(-2，0) B、(2，0) C、(-6，0) D、(6，0)4. 端午节前夕，在东昌湖举行的全民健身运动会龙舟比赛中，甲、，乙两队在500米的赛道上，所划行的路程y(m)与时间x(min)之间的函数关系式如图所示，下列说法错误的是（ ）
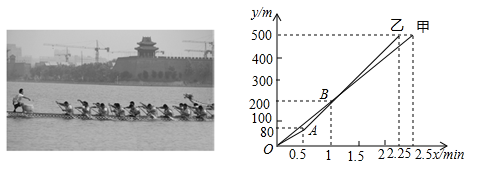A、乙队比甲队提前0.25min到达终点 B、当乙队划行110 m时，此时落后甲队15 m C、0.5 min后，乙队比甲队每分钟快40 m D、自1.5min开始，甲队若要与乙队同时到达终点，甲队的速度需提高到255m/min5. 如图所示，若直线PA的解析式为y= x+b，且点P的坐标为(4，2)，PA=PB，则点B的坐标为（ ）
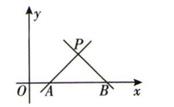A、(5，0) B、(6，0) C、(7，0) D、(8，0)6. 小李以每千克0.8元的价格从批发市场购进若干千克西瓜到市场去销售，在销售完部分西瓜之后，余下的每千克降价0.4元，最后全部售完.销售金额与卖瓜的千克数之间的关系如图所示，试问小李盈利（ ）
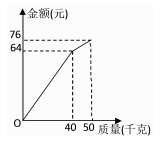A、32元 B、36元 C、38元 D、44元7. 如图所示，l甲 ， l乙分别是甲、乙两弹簧的长y(cm) 与所挂物体质量x(kg)之间函数关系的图象，设甲弹簧每挂1kg物体伸长的长度为k甲cm，乙弹．簧每挂1kg物体伸长的长度为k乙cm，则k甲与k乙的关系是（ ）
A、k甲>k乙 B、k甲=k乙 C、k甲<k乙 D、不能确定8. 如图所示，l1反映了某公司的销售收入与销售量的关系，l2反映了该公司产品的销售成本与销售量的关系，当该公司盈利(收入大于成本)时，销售量（ ）
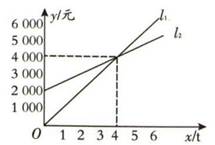A、小于3 t B、大于3 t C、小于4 t D、大于4 t9. 一次函数y=kx+b的图象如图所示，则下列结论正确的是（ ）
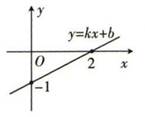A、k<0 B、b=-1 C、y随x的增大而减小 D、当x>2时，kx+b<010. 一家游泳馆的游泳收费标准为30元/次，若购买会员年卡，可享受如下优惠：会员年卡类型
办卡费用/元
每次游泳收费/元
A类
50
25
B类
200
20
C类
400
15
例如，购买A类会员年卡，一年内游泳20次，消费50+25×20=550(元)，若一年内在该游泳馆游泳的次数介于45~55次之间，则最省钱的方式为（ ）
A、购买A类会员年卡 B、购买B类会员年卡 C、购买C类会员年卡 D、不购买会员年卡二、填空题
-
11. 如图所示，已知一次函数y=kx+5和y=-x+b的图象交于点P(3，7)．则关于x的方程kx+5=-x+b的解是
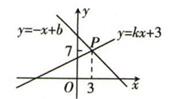12. 一次函数y=kx+b的图象经过(-3，7)，则方程kx+b=7的解为13. 某农科所为定点帮扶村免费提供一种优质瓜苗及大棚栽培技术．这种瓜苗早期在农科所的温室中生长，长到大约20 cm时移至大棚内，沿插杆继续向上生长．研究表明，60天内，这种瓜苗生长的高度y(cm)与生长时间x(天)之间的关系大致如图所示．当这种瓜苗长到大约80cm时，开始开花结果，试求这种瓜苗移至大棚后，继续生长大约天，开始开花结果．
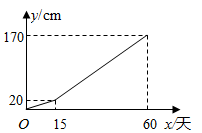14. 一次越野跑中，当小明跑了1600米时，小刚跑了1400米，小明、小刚在此后所跑的路程y(米)与时间t(秒)之间的函数关系如图所示，则这次越野跑的全程为米．
15. A，B两地相距20 km，甲、乙两人沿同一条路线从A地到B地，甲先出发，匀速行驶．甲出发1小时后乙再出发．乙以2 km/h的速度匀速行驶1小时后提高速度并继续匀速行驶，结果比甲提前到达．甲、乙两人离开A地的距离y(km)与时间t(h)的关系如图所示，则甲出发小时后和乙相遇．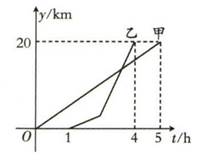
三、解答题
-
16. 在“新冠”疫情期间，全国人民“众志成城，同心抗疫”，某商家决定将一个月获得的利润全部捐赠给社区用于抗疫。已知商家购进一批产品，成本为10元/件，拟采取线上和线下两种方式进行销售。调查发现，线下的月销量y(单位：件)与线下售价x(单位：元/件，12≤x<24)满足一次函数的关系，部分数据如下表：
x(元/件)
12
13
14
15
16
y(件)
1200
1100
1000
900
800
求y与x的函数关系式．
17. 直线y=kx+b与直线y=5-4x平行，且与直线y=-3(x-6)相交，交点在y轴上，求此直18. 已知直线y=kx+b与直线y=2x平行，且它与直线y=5x+4的交点在y轴上，求其对应的函数表达式．19. 如图所示，汽车油箱的余油量y(L)与汽车的行驶时间x(h)的关系为一次函数，由此可知，汽车行驶的最长时间是多少？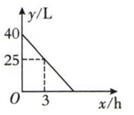
20. 校园美术活动社为筹备公益基金，向外出售自制环保手工艺品，A种手工艺品每件成本20元，售价30元；B种手工艺品每件成本35元，售价48元，活动社准备拿出800元作为制作成本，怎样制作才能使销售这两种手工艺品的利润最大？(其中B种商品不少于7件)21. 在弹性限度内，弹簧的长度y(cm)是所挂物体质量x(kg)的一次函数．某弹簧不挂物体时长14.5cm；当所挂物体的质量为3kg时，弹簧长16cm．写出y与x之间的函数关系式，并求出所挂物体的质量为4 kg时弹簧的长度．22. 如图所示，函数y=2x与y=ax+4的图象交于点A(m，3)，求方程2x=ax+4的解．
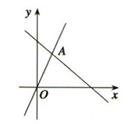23.A、B两城相距600千米，一辆客车从A城开往B城，车速为每小时80千米，同时一辆出租车从B城开往A城，车速为毎小时100千米，设客车出时间为t．
探究 若客车、出租车距B城的距离分别为y1、y2 ， 写出y1、y2关于t的函数关系式，并计算当y1=200千米时
y2的值．
发现 设点C是A城与B城的中点，
（1）哪个车会先到达C？该车到达C后再经过多少小时，另一个车会到达C？
（2）若两车扣相距100千米时，求时间t．
决策 已知客车和出租车正好在A，B之间的服务站D处相遇，此时出租车乘客小王突然接到开会通知，需要立即返回，此时小王有两种选择返回B城的方案：
方案一：继续乘坐出租车，到达A城后立刻返回B城（设出租车调头时间忽略不计）；
方案二：乘坐客车返回城．
试通过计算，分析小王选择哪种方式能更快到达B城？
