(鲁教版)2022-2023学年度第一学期七年级数学6.1函数 同步测试
试卷更新日期:2022-10-26 类型:同步测试
一、单选题
-
1. 如图,是某蓄水池的横断面示意图,分深水区和浅水区,如果向这个蓄水池以固定的流量注水,图中哪个图像能大致表示水的最大深度和时间之间的函数关系( )
 A、
A、 B、
B、 C、
C、 D、
D、 2. 下列各图表示y是x的函数的图象是( )A、
2. 下列各图表示y是x的函数的图象是( )A、 B、
B、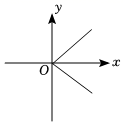 C、
C、 D、
D、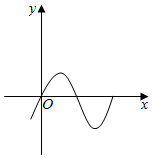 3. 根据流程图中的程序,当输出数值 为 时,输入的数值 为( )
3. 根据流程图中的程序,当输出数值 为 时,输入的数值 为( ) A、2 B、-2 C、-2或2 D、6或24. 从某容器口以均匀地速度注人酒精,若液面高度h随时间t的变化情况如图所示,则对应容器的形状为( )
A、2 B、-2 C、-2或2 D、6或24. 从某容器口以均匀地速度注人酒精,若液面高度h随时间t的变化情况如图所示,则对应容器的形状为( ) A、
A、 B、
B、 C、
C、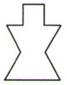 D、
D、 5. 把一个长为8,宽为3的长方形的宽增加x(0≤x<5),长不变,所得长方形的面积y与x的函数表达式为( )A、y=24-x B、y=8x-24 C、y=8x D、y=8x+246. 已知正比例函数y=3x的图象经过点(1,m),则m的值为( )A、 B、3 C、 D、-37. 下列关系式:①x-3x=4;②s=3.5t;③y=-2x;④y=5x-3;⑤C= 2πr;⑥y2=-2x.其中是函数关系的有( )A、①⑥ B、②③④⑤ C、④⑥ D、①②8. 用m元钱在网上书店恰好可购买100本书,但是每本书需另加邮寄费6角,购买n本书共需费用y元,则可列出关系式( )A、y=n( +0.6) B、y=n( )+0.6 C、y=n( +0.6) D、y=n( )+0.69. 下列不是函数关系的是( )A、y=± (x>0) B、y= (x>0) C、y=2 (x>0) D、y=- (x>0)10. 定义新运算:a&b= ,
5. 把一个长为8,宽为3的长方形的宽增加x(0≤x<5),长不变,所得长方形的面积y与x的函数表达式为( )A、y=24-x B、y=8x-24 C、y=8x D、y=8x+246. 已知正比例函数y=3x的图象经过点(1,m),则m的值为( )A、 B、3 C、 D、-37. 下列关系式:①x-3x=4;②s=3.5t;③y=-2x;④y=5x-3;⑤C= 2πr;⑥y2=-2x.其中是函数关系的有( )A、①⑥ B、②③④⑤ C、④⑥ D、①②8. 用m元钱在网上书店恰好可购买100本书,但是每本书需另加邮寄费6角,购买n本书共需费用y元,则可列出关系式( )A、y=n( +0.6) B、y=n( )+0.6 C、y=n( +0.6) D、y=n( )+0.69. 下列不是函数关系的是( )A、y=± (x>0) B、y= (x>0) C、y=2 (x>0) D、y=- (x>0)10. 定义新运算:a&b= ,例如:3&4=12,3&(-4)=12,则函数y=2&x(x≠0)的图象大致是( )
A、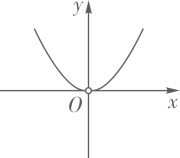 B、
B、 C、
C、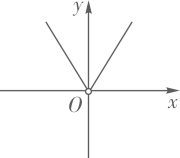 D、
D、
二、填空题
-
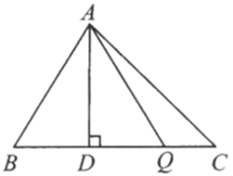
11. 如图所示,在三角形 中,已知 ,高 ,动点 由点 沿 向点 移动 不与点 重合 设 的长为 ,三角形 的面积为 ,则 与 之间的关系式为 .
 12. 已知y与x+1成正比例,比例系数是2,则y与x的函数关系式是13. 已知y=x2+3x,当x=-2时,y=14. 已知y+2与x-1成正比例关系,且当x=3时,y=2,则当y=3时,x= .15. 根据如图所示程序计算函数值,若输人的x的值为 ,则输出的函数值为
12. 已知y与x+1成正比例,比例系数是2,则y与x的函数关系式是13. 已知y=x2+3x,当x=-2时,y=14. 已知y+2与x-1成正比例关系,且当x=3时,y=2,则当y=3时,x= .15. 根据如图所示程序计算函数值,若输人的x的值为 ,则输出的函数值为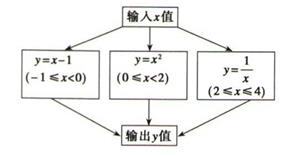
三、解答题
-
16. 随着日期的变化,国外新冠肺炎疫情形势依然严峻,结合如图的两条曲线,你能判断累计确诊人数是日期的函数吗?现有确诊人数是日期的函数吗?
 17. 骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,如图是骆驼48小时的体温随时间变化的函数图象.观察函数图象并回答:
17. 骆驼被称为“沙漠之舟”,它的体温随时间的变化而变化,如图是骆驼48小时的体温随时间变化的函数图象.观察函数图象并回答: (1)、第一天中,骆驼体温的变化范围是从℃~℃,它的体温从最低到最高经过了小时.(2)、A点表示的是什么?图像中还有什么时间的温度与A点表示的温度相同?18. 已知二次函数 .
(1)、第一天中,骆驼体温的变化范围是从℃~℃,它的体温从最低到最高经过了小时.(2)、A点表示的是什么?图像中还有什么时间的温度与A点表示的温度相同?18. 已知二次函数 .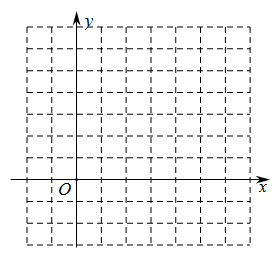 (1)、二次函数 的图象与 轴交于 、 两点( 点在 点左侧),求 、 两点的坐标;(2)、在网格中,画出该函数的图象.19. 已知菱形的两条对角线长分别为y与x,且菱形的面积为10,请求出y与x的函数关系式并计算当x=5时,y的值.20. 函数 与函数 ( 、 为不等于零的常数)的图像有一个公共点 ,其中正比例函数 的值随 的值增大而减小,求这两个函数的解析式.21. 已知y=y1-y2 , y1与x成反比例,y2与x-2成正比例,并且当x=2时,y=5;当x=1时,y=-1.当x=-1时,求y的值.22. 已知一次函数 ,当 时 的值为 ,当 时 的值为 ,求一次函数解析式,并画出函数的图象.23. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.
(1)、二次函数 的图象与 轴交于 、 两点( 点在 点左侧),求 、 两点的坐标;(2)、在网格中,画出该函数的图象.19. 已知菱形的两条对角线长分别为y与x,且菱形的面积为10,请求出y与x的函数关系式并计算当x=5时,y的值.20. 函数 与函数 ( 、 为不等于零的常数)的图像有一个公共点 ,其中正比例函数 的值随 的值增大而减小,求这两个函数的解析式.21. 已知y=y1-y2 , y1与x成反比例,y2与x-2成正比例,并且当x=2时,y=5;当x=1时,y=-1.当x=-1时,求y的值.22. 已知一次函数 ,当 时 的值为 ,当 时 的值为 ,求一次函数解析式,并画出函数的图象.23. 在“看图说故事”活动中,某学习小组结合图象设计了一个问题情境.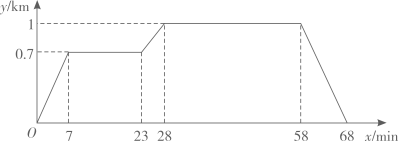
已知小亮所在学校的宿舍、食堂、图书馆依次在同一条直线上,食堂离宿舍 ,图书馆离宿舍 .周末,小亮从宿舍出发,匀速走了 到食堂;在食堂停留 吃早餐后,匀速走了 到图书馆;在图书馆停留 借书后,匀速走了 返回宿舍,给出的图象反映了这个过程中小亮离宿舍的距离 与离开宿舍的时间 之间的对应关系.
请根据相关信息,解答下列问题:
(1)、填表:离开宿舍的时间/
2
5
20
23
30
离宿舍的距离/
0.2
0.7
(2)、填空:①食堂到图书馆的距离为 .
②小亮从食堂到图书馆的速度为 .
③小亮从图书馆返回宿舍的速度为 .
④当小亮离宿舍的距离为 时,他离开宿舍的时间为 .
(3)、当 时,请直接写出y关于x的函数解析式.