（鲁教版）2022-2023学年度第一学期七年级数学5.3轴对称与坐标变化 同步测试
试卷更新日期：2022-10-26 类型：同步测试
一、单选题
-
1. 若点P（－2，1）关于y轴的对称点为Q（a，b），则点Q的坐标为（ ）A、（2，1） B、（－2，－1） C、（2，－1） D、（－2，1）2. 将△ABC的三个顶点坐标的横坐标都乘-1，并保持纵坐标不变，则所得图形与原图形的关系是（ ）
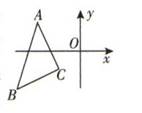A、关于x轴对称 B、关于y轴对称 C、关于原点对称 D、将原图形沿x轴的负方向平移了1个单位3. 如图所示，在平面直角坐标系中，点P(-1，2)关于直线x=1的对称点的坐标为（ ）
A、(1，2) B、(2，2) C、(3，2) D、(4，2)4. 如图，在平面直角坐标系中，对△ABC进行循环往复的轴对称变换，若原来点A坐标是(1，2)，则经过第2021次变换后点A的对应点的坐标为（ ）
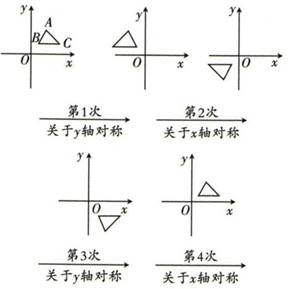A、(1，-2) B、(-1，-2) C、(-1，2) D、(1，2)5. 若点A(1+m，1-n)与点B(-3，2)关于y轴对称，则m+n的值是（ ）A、-5 B、-3 C、3 D、16. 如图所示，在平面直角坐标系中，△ABC位于第二象限，点A的坐标是(-2，3)，作△ABC关于y轴对称的△A1B1C1 ， 再作与△A1B1C1关于x轴对称的△A2B2C2 ， 则点A的对应点A2的坐标是（ ）
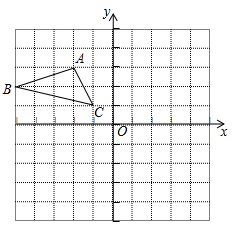A、(-3，2) B、(2，-3) C、(1，-2) D、(-1， 2)7. 在平面直角坐标系中，已知点A(-4，3)与点B关于y轴对称，则点B的坐标为（ ）A、(-4，-3) B、(4，3) C、(4，-3) D、(-4，3)8. 在直角坐标系中，点A(1，2)的横坐标乘-1，纵坐标不变，得到A'点，则点A与点A'的关系是（ ）A、关于x轴对称 B、关于y轴对称 C、没有对称关系 D、将A点向x轴的负方向平移1个单位长度9. 如图所示，正五边形ABCDE放入某平面直角坐标系后，若顶点A，B，C，D的坐标分别是(0，a)，(-3，2)，(b，m)，(c，m)，则点E的坐标是（ ）
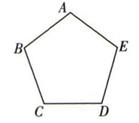A、(2，-3) B、(2，3) C、(3，2) D、(3，-2)10. 如图，△ABC的顶点都在正方形网格格点，上，点A的坐标为(-1，4)．将△ABC沿y轴翻折到第一象限，则点C的对应点C'的坐标是（ ）
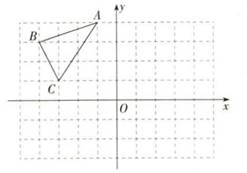A、(3，1) B、(-3，-1) C、(1，-3) D、(3，-1)二、填空题
-
11. 若在y轴上，则点P关于x轴的对称点的坐标是 ．12. 在平面直角坐标系xOy中，已知点A(1，0)，点B(-4，0)，直线l经过点A且与x轴垂直．若点B关于y轴的对称点是B1 ， 点B1关于直线l的对称点是B2 ， 则点B2的坐标是
13. 如图所示，点P(-2，1)与点Q(a，b)关于直线l(y=-1)对称，则a+b=
14. 在平面直角坐标系中，点A的坐标是(a，3)，点B的坐标是(4，b)，若点A与点B关于x轴对称，则ab=15. 在平面直角坐标系中，点A的坐标是(-1，2)，作点A关于y轴的对称点，得到点A'，再作点A'关于x轴对称的点A"，则点A”的坐标是三、解答题
-
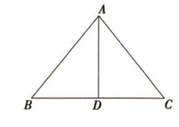
16. 如图所示，已知在△ABC中，AB=AC，BC=6，BC边上的高AD垂直平分BC，且AD=4，建立适当的平面直角坐标系，并求这个三角形三个顶点的坐标．
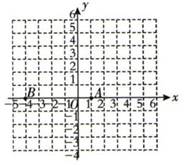
17.（1）请画出△ABC关于y轴对称的△A′B′C′（其中A′，B′，C′分别是A，B，C的对应点，不写画法）；
（2）直接写出A′，B′，C′三点的坐标：
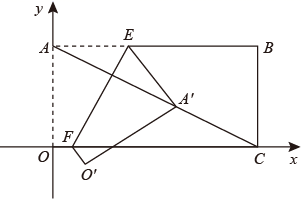
（3）计算△ABC的面积．18. 如图，平面直角坐标系中，点A（0，3）和B（4，0），点M（8，m）为坐标平面内一动点，且△ABM为等腰三角形，求点M的坐标，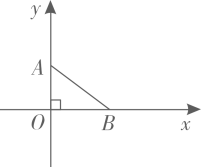
19. 如图，在平面直角坐标系中，的顶点 ， 在坐标轴上， ， ， ， 求所在直线的解析式.
20. 如图，在平面直角坐标系中，A(﹣3，2)，B(﹣4，﹣3)，C(﹣1，﹣1)．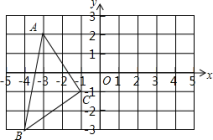
⑴在图中作出关于y轴对称的；
⑵写出点的坐标（直接写答案）；
⑶在y轴上画出点P，使PB+PC最小．
