沪科版数学2022~2023学年年度九年级(上)期中考试模拟卷(A卷)
试卷更新日期:2022-10-26 类型:期中考试
一、单选题(每题4分,共40分)
-
1. 下列函数中,是二次函数的是( )A、 B、 C、 D、2. 把抛物线y=-x2的图象向左平移1个单位,然后向上平移3个单位,则平移后的图象对应的二次函数的关系式为( )A、y=-(x+1)2+3 B、y=-(x+1)2-3 C、y=-(x-1)2-3 D、y=-(x-1)2+33. 已知二次函数的图象上有三点 , , , 则、、的大小关系为( )A、 B、 C、 D、4. 已知二次函数y=kx2-7x-7的图象和×轴有交点,则k的取值范围是( )A、k> B、k≥ C、k≥且k≠0 D、k> 且k≠05. 宽与长的比是(约为0.618)的矩形叫黄金矩形,黄金矩形给我们以协调、匀称的美感.世界各国许多著名的建筑,为取得最佳的视觉效果,都采用了黄金矩形的设计,如希腊的巴特神庙等.若黄金矩形的长为 , 则该黄金矩形的宽是( )A、 B、 C、 D、6. 在同一直角坐标系中,函数和函数(a是常数,且a≠0)的图象可能是( )A、
 B、
B、 C、
C、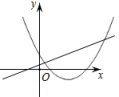 D、
D、 7. 如图,有一抛物线形拱桥,当拱顶离水面 时,水面宽 ,当水面宽增加 时,则水面应下降的高度是( )
7. 如图,有一抛物线形拱桥,当拱顶离水面 时,水面宽 ,当水面宽增加 时,则水面应下降的高度是( ) A、 B、 C、 D、8. 如图,四边形中, , 交轴正半轴于点 , 反比例函数经过点 , 交的中点于 , 平分 , 若 , 则的值为( )
A、 B、 C、 D、8. 如图,四边形中, , 交轴正半轴于点 , 反比例函数经过点 , 交的中点于 , 平分 , 若 , 则的值为( ) A、12 B、 C、8 D、9. 如图,在 中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E , 若BE=1,则EC=( )
A、12 B、 C、8 D、9. 如图,在 中,D在AC边上,AD:DC=1:2,O是BD的中点,连接AO并延长交BC于E , 若BE=1,则EC=( ) A、 B、2 C、3 D、410. 抛物线的对称轴是直线 , 且过点 , 顶点位于第二象限,其部分图像如图所示,给出以下判断:①且;②;③;④;⑤直线与抛物线两个交点的横坐标分别为 , 则 . 其中正确的个数有( )
A、 B、2 C、3 D、410. 抛物线的对称轴是直线 , 且过点 , 顶点位于第二象限,其部分图像如图所示,给出以下判断:①且;②;③;④;⑤直线与抛物线两个交点的横坐标分别为 , 则 . 其中正确的个数有( ) A、1个 B、3个 C、5个 D、2个
A、1个 B、3个 C、5个 D、2个二、填空题(共5题,共25分)
-
11. 抛物线y=+bx+c,经过A(-1,0),B(3,0)两点,则这条抛物线的解析式为.12. 如图,直线与双曲线的图象在第一象限内交于点 , 过点的另一直线交双曲线于第三象限内的点 , 则不等式的解集是 .
 13. 如图,是一个迷宫游戏盘的局部平面简化示意图,该矩形的长、宽分别为5cm,3cm,其中阴影部分为迷宫中的挡板,设挡板的宽度为xcm,小球滚动的区域(空白区域)面积为ycm2 . 则y关于x的函数关系式为:(化简为一般式).
13. 如图,是一个迷宫游戏盘的局部平面简化示意图,该矩形的长、宽分别为5cm,3cm,其中阴影部分为迷宫中的挡板,设挡板的宽度为xcm,小球滚动的区域(空白区域)面积为ycm2 . 则y关于x的函数关系式为:(化简为一般式).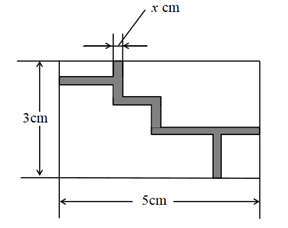 14. 如图,在等腰 中, ,点P在 的延长线上, ,点D在 边上, ,则 的值是.
14. 如图,在等腰 中, ,点P在 的延长线上, ,点D在 边上, ,则 的值是. 15. 抛物线 与线段 有两个不同的交点,已知 , ,则 的取值范围是 .
15. 抛物线 与线段 有两个不同的交点,已知 , ,则 的取值范围是 .三、综合题(共8题,共85分)
-
16. 从地面竖直向上抛出一小球,小球的高度 (单位: )与小球的运动时间 (单位: )之间的关系式是 ( ).求小球运动时间是多少时,小球最高?小球运动中的最大高度是多少?17. 已知 、 、 是 的三边长,且 .(1)、求 的值;(2)、若 的周长为90,求各边的长.18. 如图,正比例函数与反比例函数的图象交于 , 两点.
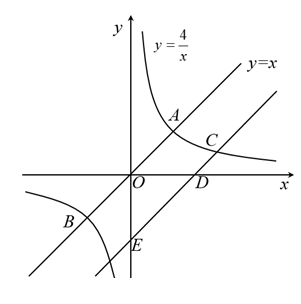 (1)、求 , 两点的坐标;(2)、将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点 , 与轴交于点 , 与轴交于点 , 若 , 求的值.19. 如图,矩形ABCD的长AD=5 cm,宽AB=3 cm,长和宽都增加x cm,那么面积增加y cm2.
(1)、求 , 两点的坐标;(2)、将直线向下平移个单位长度,与反比例函数在第一象限的图象交于点 , 与轴交于点 , 与轴交于点 , 若 , 求的值.19. 如图,矩形ABCD的长AD=5 cm,宽AB=3 cm,长和宽都增加x cm,那么面积增加y cm2.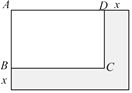 (1)、写出y与x的函数关系式;
(1)、写出y与x的函数关系式;
(2)、当增加的面积y=20 cm2时,求相应的x是多少?
20. 学生上课时注意力集中的程度可以用注意力指数表示.某班学生在一节数学课中的注意力指数y随上课时间x(分钟)的变化图象如图.上课开始时注意力指数为30,第2分钟时注意力指数为40,前10分钟内注意力指数y是时间x的一次函数.10分钟以后注意力指数y是x的反比例函数. (1)、当0≤x≤10时,求y关于x的函数关系式;(2)、当10≤x≤40时,求y关于x的函数关系式;(3)、如果讲解一道较难的数学题要求学生的注意力指数不小于50,为了保证教学效果本节课讲完这道题不能超过多少分钟?21. 公路上正在行驶的甲车发现前方处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程单位:、速度单位:与时间单位:的关系分别可以用二次函数和一次函数表示,其图象如图所示.
(1)、当0≤x≤10时,求y关于x的函数关系式;(2)、当10≤x≤40时,求y关于x的函数关系式;(3)、如果讲解一道较难的数学题要求学生的注意力指数不小于50,为了保证教学效果本节课讲完这道题不能超过多少分钟?21. 公路上正在行驶的甲车发现前方处沿同一方向行驶的乙车后,开始减速,减速后甲车行驶的路程单位:、速度单位:与时间单位:的关系分别可以用二次函数和一次函数表示,其图象如图所示.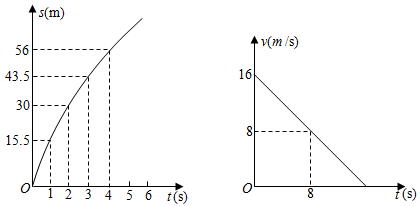 (1)、直接写出关于的函数关系式和关于的函数关系式不要求写出的取值范围(2)、当甲车减速至时,它行驶的路程是多少?(3)、若乙车以的速度匀速行驶,两车何时相距最近,最近距离是多少?22. 冰墩墩是北京2022年冬季奥运会吉祥物.该吉祥物以熊猫为原型进行设计创作,将熊猫形象与富有超能量的冰晶外壳相结合,体现了冬季冰雪运动和现代科技特点,冰墩墩挂件也很受欢迎,某小店的进货价为每个50元,当售价为每个92元时,每月可销售100个,为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售10个.设每个挂件的售价为x元(x为正整数且),每月的销售量为y个.(1)、当售价为85时,每个月的销售量为;(2)、设该店每月所获利润为w元,当降价多少元时,每月所获利润最大,最大利润是多少?(3)、该店店主热心公益事业,决定每月从出售的每个挂件中拿出6元资助贫困学生,且总捐款额不低于1500元,求捐款后每月最大利润.23. 如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).
(1)、直接写出关于的函数关系式和关于的函数关系式不要求写出的取值范围(2)、当甲车减速至时,它行驶的路程是多少?(3)、若乙车以的速度匀速行驶,两车何时相距最近,最近距离是多少?22. 冰墩墩是北京2022年冬季奥运会吉祥物.该吉祥物以熊猫为原型进行设计创作,将熊猫形象与富有超能量的冰晶外壳相结合,体现了冬季冰雪运动和现代科技特点,冰墩墩挂件也很受欢迎,某小店的进货价为每个50元,当售价为每个92元时,每月可销售100个,为了吸引更多顾客,该网店采取降价措施.据市场调查反映:销售单价每降1元,则每月可多销售10个.设每个挂件的售价为x元(x为正整数且),每月的销售量为y个.(1)、当售价为85时,每个月的销售量为;(2)、设该店每月所获利润为w元,当降价多少元时,每月所获利润最大,最大利润是多少?(3)、该店店主热心公益事业,决定每月从出售的每个挂件中拿出6元资助贫困学生,且总捐款额不低于1500元,求捐款后每月最大利润.23. 如图,在平面直角坐标系中,抛物线(a≠0)的图象与x轴交于A、C两点,与y轴交于点B,其中点B坐标为(0,-4),点C坐标为(2,0).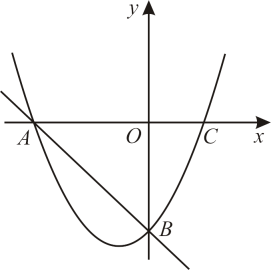 (1)、求此抛物线的函数解析式.(2)、点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)、点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.
(1)、求此抛物线的函数解析式.(2)、点D是直线AB下方抛物线上一个动点,连接AD、BD,探究是否存在点D,使得△ABD的面积最大?若存在,请求出点D的坐标;若不存在,请说明理由.(3)、点P为该抛物线对称轴上的动点,使得△PAB为直角三角形,请求出点P的坐标.