（鲁教版）2022-2023学年度第一学期六年级数学3.7探索与表达规律同步测试

试卷更新日期：2022-10-26 类型：同步测试

进入出卷网下载

一、单选题

1. 已知：2¹＝2，2²＝4，2³＝8，2⁴＝16，2⁵＝32，…，那么2²⁰²¹的个位数字是（）

A、2 B、4 C、6 D、8

查看试题解析
2. 如图，用相同的小正方形按照某种规律进行摆放，则第9个图形中小正方形的个数是（）

A、98 B、100 C、109 D、110

查看试题解析
3. 按一定规律排列的一组数据： $\frac{1}{2}$ ， $- \frac{3}{5}$ ， $\frac{1}{2}$ ， $- \frac{7}{17}$ ， $\frac{9}{26}$ ， $- \frac{11}{37}$ ， …．则按此规律排列的第10个数是（）

A、 $- \frac{19}{101}$ B、 $\frac{21}{101}$ C、 $- \frac{19}{82}$ D、 $\frac{21}{82}$

查看试题解析
4. 各正方形中的四个数之间都有一定的规律，按此规律得出 $a$ ， $b$ 的值分别为（）
0
3
2
5
4
7
6
$c$
4
13
6
31
8
57
$a$
$b$

A、9，10 B、9，91 C、10，91 D、10，110

查看试题解析
5. 如图，在平面直角坐标系中，每个最小方格的边长均为1个单位长度，P₁ ， P₂ ， P₃ ， ……均在格点上，其顺序按图中“→”方向排列，如：P₁（0，0），P₂（0，1），P₃（1，1），P₄（1，﹣1），P₅（﹣1，﹣1），P₆（﹣1，2）……，根据这个规律，点P₂₀₂₂的坐标为（　　）

A、（﹣505，﹣505） B、（505，﹣506） C、（505，505） D、（﹣505，506）

查看试题解析
6. 在平面直角坐标系中，对 $P (x ， y)$ 作变换得到 $P^{'} (- y + 1 ， x + 1)$ ，例如： $A_{1} (3 ， 2)$ 作上述变换得到 $A_{2} (- 1 ， 4)$ ，再将 $A_{2}$ 作上述变换得到 $A_{3} (- 3 ， 0)$ ，这样依次得到 $A_{1}$ ， $A_{2}$ ， $A_{3}$ ， …， $A_{n}$ ， …，则 $A_{2022}$ 的坐标为（）

A、 $(- 1 ， 4)$ B、 $(3 ， 2)$ C、 $(- 3 ， 0)$ D、 $(1 ， - 2)$

查看试题解析
7. 观察下表，当x=7时，则y的值为（）

x

1

2

3

4

……

y

120

125

130

135

……

A、140 B、145 C、150 D、155

查看试题解析
8. 如图所示为一种“羊头"形图案.其作法如下：从正方形①开始，以它的一边为斜边向外作等腰直角三角形，然后再以等腰直角三角形的直角边为边.分别向外作正方形②和②……依此类推，若正方形①的面积为64，则正方形⑤的面积为（）

A、 $2$ B、 $4$ C、 $6$ D、 $16$

查看试题解析
9. 如图，在平面直角坐标系中，已知点 $M_{0}$ 的坐标为 $(1 ， 0)$ ，将线段 $O M_{0}$ 绕原点О逆时针方向旋转45°，再将其延长到 $M_{1}$ ，使得 $M_{1} M_{0} ⊥ O M_{0}$ ，得到线段 $O M_{1}$ ；又将线段 $O M_{1}$ 绕原点O逆时针方向旋转45°，再将其延长到 $M_{2}$ ，使得 $M_{2} M_{1} ⊥ O M_{1}$ ，得到线段 $O M_{2}$ ；如此下去，得到线段 $O M_{3}$ ， $O M_{4}$ ， $O M_{5}$ ， …根据以上规律，则点 $M_{2022}$ 的坐标为（）

A、 $(2^{1011} ， 0)$ B、 $(0 ， - 2^{2022})$ C、 $(0 ， - 2^{1011})$ D、 $(- {(\sqrt{2})}^{2021} ， - {(\sqrt{2})}^{2021})$

查看试题解析
10. 观察下列等式： $2^{1} = 2$ ， $2^{2} = 4$ ， $2^{3} = 8$ ， $2^{4} = 16$ ， $2^{5} = 32$ ， $2^{6} = 64$ ， $\cdot \cdot \cdot$ ，根据这个规律，则 $2^{1} + 2^{2} + 2^{3} + 2^{4} + \cdot \cdot \cdot + 2^{2022}$ 的末尾数字是（）

A、 $0$ B、 $2$ C、 $4$ D、 $6$

查看试题解析

二、填空题

11. 按规律填数：1，3，7，15，31，．

查看试题解析
12. 如图，一组x轴正半轴上的点 $B_{1}$ ， $B_{2}$ ， … $B_{n}$ 满足条件 $O B_{1} = B_{1} B_{2} = B_{2} B_{3} ⋯ = B_{n - 1} B_{n} = 2$ ，抛物线的顶点 $A_{1}$ ， $A_{2}$ ， … $A_{n}$ 依次是反比例函数 $y = \frac{9}{x}$ 图象上的点，第一条抛物线以 $A_{1}$ 为顶点且过点O和 $B_{1}$ ；第二条抛物线以 $A_{2}$ 为顶点且经过点 $B_{1}$ 和 $B_{2}$ ；…第n条抛物线以 $A_{n}$ 为顶点且经过点 $B_{n - 1}$ ， $B_{n}$ ，依次连结抛物线的顶点和与x轴的两个交点，形成 $△ O A_{1} B_{1}$ 、 $△ B_{1} A_{2} B_{2}$ 、…、 $△ B_{n - 1} A_{n} B_{n}$ ．请写出所有满足三角形面积为整数的n的值．

查看试题解析
13. 观察下列各式：
1³＝1²
1³+2³＝3²
1³+2³+3³＝6²
1³+2³+3³+4³＝10²
…
猜想1³+2³+3³+…+8³＝．

查看试题解析
14. 如图， $A B / / C D$ ， $P_{2} E$ 平分 $∠ P_{1} E B$ ， $P_{2} F$ 平分 $∠ P_{1} F D$ ，可得 $∠ P_{2}$ ； $P_{3} E$ 平分 $∠ P_{2} E B$ ， $P_{3} F$ 平分 $∠ P_{2} F D$ ，可得 $∠ P_{3} \dots \dots$ 设 $∠ P_{1} E B = x °$ ， $∠ P_{1} F D = y °$ ，依次平分下去，则 $∠ P_{n} =$ $° .$

查看试题解析
15. 用同样大小的黑色棋子按如图所示的规律摆放，则第n个图形有个黑色棋子．

查看试题解析

三、解答题

16. 阅读下题的计算方法：
计算 $- 5 \frac{5}{6} + (- 9 \frac{2}{3}) + 17 \frac{3}{4} + (- 3 \frac{1}{2})$ .

解：原式 $= [(- 5) + (- \frac{5}{6})] + [(- 9) + (- \frac{2}{3})] + (17 + \frac{3}{4}) + [(- 3) + (- \frac{1}{2})]$

$= [(- 5) + (- 9) + 17 + (- 3)] + [(- \frac{5}{6}) + (- \frac{2}{3}) + \frac{3}{4} + (- \frac{1}{2})]$

$= 0 + (- \frac{5}{4})$

$= - \frac{5}{4}$

上面这种解题方法叫做拆项法，按此方法计算： $(- 4 \frac{7}{8}) + (+ 8 \frac{1}{4}) + (- 3 \frac{1}{8})$

查看试题解析
17.
按如图方式摆放餐桌和椅子．用x来表示餐桌的张数，用y来表示可坐人数．
①题中有几个变量？

②你能写出两个变量之间的关系吗？

查看试题解析
18. 已知 $y_{1} = 2 x ， y_{2} = \frac{2}{y_{1}} ， y_{3} = \frac{2}{y_{2}} ， \dots ， y_{2018} = \frac{2}{y_{2017}}$ ，求 $y_{1} \cdot y_{2018}$ 的值.

查看试题解析
19. 图1中，有一个平行四边形；
图2中，由2个相同的平行四边形拼成一排的图形，这图形中可以找到3个平行四边形；
图3中，由3个相同的平行四边形拼成一排的图形，这图形中可以找到6个平行四边形；
由此我们可以提出一个这样的问题：
图4中，由4个相同的平行四边形拼成一排的图形中，可以找到几个平行四边形？
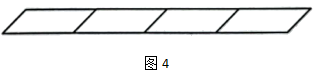
答：10个
请你根据以上事实，将一些相同的平行四边形横向或纵向拼接，由此提出一个数学问题，并写出答案．

查看试题解析
20. 判断下面各式是否成立

(1)、 $\sqrt{2 \frac{2}{3}} = 2 \sqrt{\frac{2}{3}}$ （2） $\sqrt{3 \frac{3}{8}} = 3 \sqrt{\frac{3}{8}}$ （3） $\sqrt{4 \frac{4}{15}} = 4 \sqrt{\frac{4}{15}}$
探究：①你判断完上面各题后，发现了什么规律？并猜想： $\sqrt{5 \frac{5}{24}} =_____$
②用含有n的代数式将规律表示出来，说明n的取值范围，并给出证明

查看试题解析
21. 对于密码L dp d vwxghqw，你能看出它代表什么意思吗？如果给你一把破译它的“钥匙” $x - 3$ ，联想英语宇母表中字母的顺序，你再试试能不能解读它．英语字母表中字母是按以下顺序排列的：
a b c d e f g h i j k l m n o p q r s t u v w x y z
如果规定a又接在z的后面，使26个字母排成圈，并能想到 $x - 3$ 可以代表“把一个字母换成字母表中从它向前移动3位的字母”，按这个规律就有
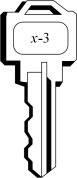
L dp d vwxghqw→I am a student.
这样你就能解读它的意思了．
为了保密，许多情况下都要采用密码，这时就需要有破译密码的“钥匙”．上面的例子中，如果写和读密码的双方事先约定了作为“钥匙”的式子 $x - 3$ 的含义，那么他们就可以用一种保密方式通信了．你和同伴不妨也利用数学式子来制定一种类似的“钥匙”，并互相合作，通过游戏试试如何进行保密通信．

查看试题解析
22. 请先阅读下列一组内容，然后解答问题：
因为： $\frac{1}{1 \times 2} = 1 - \frac{1}{2}$ ， $\frac{1}{2 \times 3} = \frac{1}{2} - \frac{1}{3}$ ， $\frac{1}{3 \times 4} = \frac{1}{3} - \frac{1}{4}$ … $\frac{1}{9 \times 10} = \frac{1}{9} - \frac{1}{10}$

所以： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{9 \times 10}$ ＝

计算： $\frac{1}{1 \times 2} + \frac{1}{2 \times 3} + \frac{1}{3 \times 4} + \dots + \frac{1}{2014 \times 2015}$ ．

查看试题解析
23. 阅读下面的材料并填空：
①（1﹣ $\frac{1}{2}$ ）（1+ $\frac{1}{2}$ ）＝1﹣ $\frac{1}{2^{2}}$ ，反过来，得1﹣ $\frac{1}{2^{2}}$ ＝（1﹣ $\frac{1}{2}$ ）（1+ $\frac{1}{2}$ ）＝ $\frac{1}{2}$ × $\frac{3}{2}$ ；
②（1﹣ $\frac{1}{3}$ ）（1+ $\frac{1}{3}$ ）＝1﹣ $\frac{1}{3^{2}}$ ，反过来，得1﹣ $\frac{1}{3^{2}}$ ＝（1﹣ $\frac{1}{3}$ ）（1+ $\frac{1}{3}$ ）＝ ▲ × ▲ ；
③（1﹣ $\frac{1}{4}$ ）（1+ $\frac{1}{4}$ ）＝1﹣ $\frac{1}{4^{2}}$ ，反过来，得1﹣ $\frac{1}{4^{2}}$ ＝ ▲ ＝ $\frac{3}{4} \times \frac{5}{4}$ ；
利用上面的材料中的方法和结论计算下题：
（1﹣ $\frac{1}{2^{2}}$ ）（1﹣ $\frac{1}{3^{2}}$ ）（1﹣ $\frac{1}{4^{2}}$ ）……（1﹣ $\frac{1}{201 6^{2}}$ ）（1﹣ $\frac{1}{201 7^{2}}$ ）（1﹣ $\frac{1}{201 8^{2}}$ ）.

查看试题解析

0	3		2	5		4	7		6	$c$
4	13		6	31		8	57		$a$	$b$

x	1	2	3	4	……
y	120	125	130	135	……

（鲁教版）2022-2023学年度第一学期六年级数学3.7探索与表达规律 同步测试

一、单选题

二、填空题

三、解答题

（鲁教版）2022-2023学年度第一学期六年级数学3.7探索与表达规律同步测试