(鲁教版)2022-2023学年度第一学期七年级数学3.3勾股定理的应用举例 同步测试
试卷更新日期:2022-10-25 类型:同步测试
一、单选题
-
1. 如图,一轮船以12海里/时的速度从港口A出发向东北方向航行,另一轮船以5海里/时的速度同时从港口A出发向东南方向航行,离开港口2小时后两船相距( )
 A、13 海里 B、16 海里 C、20 海里 D、26 海里2. 如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位: ),计算两圆孔中心A和B的距离为( )
A、13 海里 B、16 海里 C、20 海里 D、26 海里2. 如图是一个外轮廓为矩形的机器零件平面示意图,根据图中的尺寸(单位: ),计算两圆孔中心A和B的距离为( ) A、 B、 C、 D、3. 如图,长方体的长、宽、高分别是6,3,5,现一只蚂蚁从A点爬行到B点,设爬行的最短路线长为a , 则 的值是( )
A、 B、 C、 D、3. 如图,长方体的长、宽、高分别是6,3,5,现一只蚂蚁从A点爬行到B点,设爬行的最短路线长为a , 则 的值是( ) A、130 B、106 C、100 D、864. 如图,一圆柱高 ,底面半径为 ,一只蚂蚁从点 爬到点 处吃食,要爬行的最短路程( 取3)是( )
A、130 B、106 C、100 D、864. 如图,一圆柱高 ,底面半径为 ,一只蚂蚁从点 爬到点 处吃食,要爬行的最短路程( 取3)是( ) A、 B、 C、 D、无法确定5. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为8cm,则图中所有正方形的面积的和是( )
A、 B、 C、 D、无法确定5. 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为8cm,则图中所有正方形的面积的和是( ) A、192cm2 B、64cm2 C、128cm2 D、81cm26. 一根长 的吸管插入底面直径为 ,高为 的圆柱形饮料杯中,吸管露在杯子外面的长度为h , 则h的值不可能是( )A、 B、 C、 D、7. 无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有多少( )cm.
A、192cm2 B、64cm2 C、128cm2 D、81cm26. 一根长 的吸管插入底面直径为 ,高为 的圆柱形饮料杯中,吸管露在杯子外面的长度为h , 则h的值不可能是( )A、 B、 C、 D、7. 无盖圆柱形杯子的展开图如图所示.将一根长为20cm的细木筷斜放在该杯子内,木筷露在杯子外面的部分至少有多少( )cm.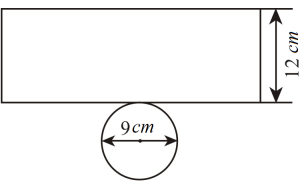 A、4 B、5 C、10 D、158. 如图,“今有竹高两丈五尺,末折抵地,去本五尺,问折者高几何?”意思是:一根竹子,原来高两丈五尺(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部五尺远,则折断处离地面的高度为( )
A、4 B、5 C、10 D、158. 如图,“今有竹高两丈五尺,末折抵地,去本五尺,问折者高几何?”意思是:一根竹子,原来高两丈五尺(一丈为十尺),虫伤有病,一阵风将竹子折断,其竹梢恰好抵地,抵地处离原竹子根部五尺远,则折断处离地面的高度为( ) A、12尺 B、13尺 C、15尺 D、25尺9. 如图,长方形门框高为2m,宽为1.5m,现有3块木板,尺寸如下:①号木板长3m,宽2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.6m.能从这扇门通过的木板是( )
A、12尺 B、13尺 C、15尺 D、25尺9. 如图,长方形门框高为2m,宽为1.5m,现有3块木板,尺寸如下:①号木板长3m,宽2.7m;②号木板长4m,宽2.4m;③号木板长2.8m,宽2.6m.能从这扇门通过的木板是( ) A、① B、② C、③号 D、都不能通过10. 如图所示,在长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1,一只蚂蚁从A点出发,沿长方体表面爬到C1点处觅食,则蚂蚁所行路程的最小值的平方为( )
A、① B、② C、③号 D、都不能通过10. 如图所示,在长方体ABCD-A1B1C1D1中,AB=3,BC=2,BB1=1,一只蚂蚁从A点出发,沿长方体表面爬到C1点处觅食,则蚂蚁所行路程的最小值的平方为( ) A、14 B、18 C、20 D、26
A、14 B、18 C、20 D、26二、填空题
-
11. 如图,学校有一块长方形花圃,有极少数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,踩伤了花草.则他们仅仅少走了 步路.(假设2步为1米)
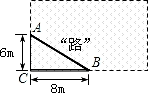 12. 如图,小明站在离水面高度为8米的岸上点C处用绳子拉船靠岸,开始时绳子的长为17米,小明以1米每秒的速度收绳,7秒后船移动到点D的位置,问船向岸边移动了米(的长)(假设绳子是直的).
12. 如图,小明站在离水面高度为8米的岸上点C处用绳子拉船靠岸,开始时绳子的长为17米,小明以1米每秒的速度收绳,7秒后船移动到点D的位置,问船向岸边移动了米(的长)(假设绳子是直的). 13. 如图,一棵高为16m的大树被台风刮断,若树在离地面6m处折断,树顶端刚好落在地上,此处离树底部m处.
13. 如图,一棵高为16m的大树被台风刮断,若树在离地面6m处折断,树顶端刚好落在地上,此处离树底部m处. 14. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 ,对角线 、 交于点 .若 , ,则 .
14. 对角线互相垂直的四边形叫做“垂美”四边形,现有如图所示的“垂美”四边形 ,对角线 、 交于点 .若 , ,则 . 15. 国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是 .
15. 国庆假期中,小华与同学去玩探宝游戏,按照探宝图,他们从门口A处出发先往东走8km,又往北走2km,遇到障碍后又往西走3km,再向北走到6km处往东拐,仅走了1km,就找到了宝藏,则门口A到藏宝点B的直线距离是 .
三、解答题
-
16. 如图,湖的两岸有A , B两点,在与AB成直角的BC方向上的点C处测得 米, 米.求A , B两点间的距离.
 17. 如图,高速公路上有A,B两点相距10km,C,D为两村庄,已知DA=4km,CB=6km,DA⊥AB于点A,CB⊥AB于B,现要在AB上建一个服务站E,使得C,D两村庄到E站的距离相等,求BE的长.
17. 如图,高速公路上有A,B两点相距10km,C,D为两村庄,已知DA=4km,CB=6km,DA⊥AB于点A,CB⊥AB于B,现要在AB上建一个服务站E,使得C,D两村庄到E站的距离相等,求BE的长. 18. 如图所示,一桥洞的上边是半圆,下边是长方形.已知半圆的直径为2m,长方形的另一边是1m,有一辆厢式小货车,高1.5米,宽1.6米,这辆小货车能否通过此桥洞?通过计算说明理由.
18. 如图所示,一桥洞的上边是半圆,下边是长方形.已知半圆的直径为2m,长方形的另一边是1m,有一辆厢式小货车,高1.5米,宽1.6米,这辆小货车能否通过此桥洞?通过计算说明理由. 19. 如图,一个牧童在小河的南4华里(长度单位)的A处牧马,而他正位于他的小屋B的西8华里北7华里处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?
19. 如图,一个牧童在小河的南4华里(长度单位)的A处牧马,而他正位于他的小屋B的西8华里北7华里处,他想把他的马牵到小河边去饮水,然后回家,他要完成这件事情所走的最短路程是多少?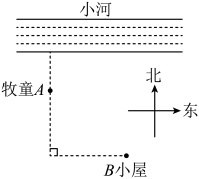 20. 我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是多少尺?
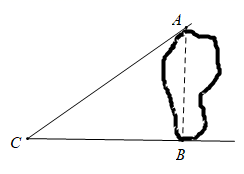
20. 我国古代有这样一道数学问题:“枯木一根直立地上,高二丈,周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?”题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则问题中葛藤的最短长度是多少尺? 21. 如图所示,在一棵树的10 m高的B处有两只猴子,其中一只猴子爬下树,走到离树20 m的池塘A处,另一只猴子爬到树顶D后直接跃向池塘A处,如果两只猴子所经过的距离相等,求这棵树的高度.
21. 如图所示,在一棵树的10 m高的B处有两只猴子,其中一只猴子爬下树,走到离树20 m的池塘A处,另一只猴子爬到树顶D后直接跃向池塘A处,如果两只猴子所经过的距离相等,求这棵树的高度.

