（鲁教版）2022-2023学年度第一学期八年级数学3.4数据的离散程度 同步测试

试卷更新日期：2022-10-25 类型：同步测试

进入 出卷网 下载

一、单选题

  • 1. 若一组数据7，15，10，5，x，20的平均数是10，则这组数据的极差是（   ）
    A、10 B、13 C、15 D、17

    查看试题解析

  • 2. 甲、乙、丙、丁四名学生近4次数学测验成绩的平均数都是90分，方差分别是S甲2＝5，S乙2＝20，S丙2＝23，S丁2＝32，则这四名学生的数学成绩最稳定的是（   ）
    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 3. 甲、乙、丙、丁4名同学参加跳远测试各10次，他们的平均成绩及方差如表：

    测试者

    平均成绩（单位：m）

    方差

    甲

    6.2

    0.25

    乙

    6.0

    0.58

    丙

    5.8

    0.12

    丁

    6.2

    0.32

    若从其中选出1名成绩好且发挥稳定的同学参加学校运动会，则应选（    ）

    A、甲 B、乙 C、丙 D、丁

    查看试题解析

  • 4. 小强每天坚持做引体向上的锻炼，下表是他记录的某一周每天做引体向上的个数.

    星期

    日

    一

    二

    三

    四

    五

    六

    个数

    11

    12

    10

    13

    13

    13

    12

    对于小强做引体向上的个数，下列说法错误的是（   ）

    A、平均数是12 B、众数是13 C、中位数是12.5 D、方差是87

    查看试题解析

  • 5. 一城市准备选购一千株高度大约为2m的某种风景树来进行街道绿化，有四个苗圃生产基地投标（单株树的价格都一样）．采购小组从四个苗圃中都任意抽查了20株树苗的高度，得到的数据如下：

    树苗平均高度（单位：m）

    标准差

    甲苗圃

              1.8

     0.2

    乙苗圃

              1.8

     0.6

    丙苗圃

              2.0

     0.6

    丁苗圃

              2.0

     0.2

    请你帮采购小组出谋划策，应选购（   ）

    A、甲苗圃的树苗 B、乙苗圃的树苗； C、丙苗圃的树苗 D、丁苗圃的树苗

    查看试题解析

  • 6. 一次排球比赛中，某球队6名场上队员的身高（单位： cm ）分别是181，185，189，191，193，195．现用一名身高为 183cm 的队员换下场上身高为 195cm 的队员，则场上队员的身高（    ）
    A、平均数变小，方差变小 B、平均数变小，方差变大 C、平均数变大，方差变小 D、平均数变大，方差变大

    查看试题解析

  • 7. 某班有50人，一次数学测试后，老师对测试成绩进行了统计．由于小颖没有参加此次集体测试，因此计算其他49人的平均分为92分，方差s2＝23．后来小颖进行了补测，成绩是92分，关于该班50人的数学测试成绩，下列说法正确的是（    ）
    A、平均分不变，方差变小 B、平均分不变，方差变大 C、平均分和方差都不变 D、平均分和方差都改变

    查看试题解析

  • 8. 已知一组数据a，b，c的平均数为6，方差为4.1，那么数据a−2 ， b−2 ， c−2的平均数和方差分别是（ ）
    A、4，2.1 B、4，4.1 C、6，2.1 D、6，4.1

    查看试题解析

  • 9. 一组数据a－1、b－1、c－1、d－1、e－1、f－1、g－1的平均数是m，方差是n，则另一组数据2a－3、2b－3、2c－3、2d－3、2e－3、2f－3、2g－3的平均数和方差分别是（    ）
    A、2m－3、2n－3 B、2m－1、4n C、2m－3、2n D、2m－3、4n

    查看试题解析

  • 10. 已知样本x1 ， x2 ， x3 ， …，xn的方差是1，则样本2x1+3 ， 2x2+3 ， 2x3+3 ， …，2xn+3的方差是（ ）
    A、1 B、2 C、3 D、4

    查看试题解析

二、填空题

  • 11. 一组数据﹣1、2、3、4的极差是 ．

    查看试题解析

  • 12. 甲、乙两名篮球运动员进行每组10次的投篮训练，5组投篮结束后，两人的平均命中数都是7次，方差分别是S甲2=1.4 ， S乙2=0.85 ， 则在本次训练中，运动员的成绩更稳定．

    查看试题解析

  • 13. 甲、乙两人在相同条件下进行射击练习，每人10次射击成绩的平均数都是8环，方差分别为S甲2＝1.4，S乙2＝0.6，则两人射击成绩比较稳定的是 （填“甲”或“乙”）．

    查看试题解析

  • 14. 跳远运动员李强在一次训练中，先跳了6次的成绩如下：7.6，7.8，7.7，7.8，8.0，7.9（单位：m）．这六次成绩的平均数为7.8，方差为 160 ．如果李强再跳两次，成绩分别为7.6，8.0，则李强这8次跳远成绩与前6次的成绩相比较，其方差 ． （填“变大”、“不变”或“变小”）

    查看试题解析

  • 15. 在方差计算公式 s2=120[(x1−15)2+(x2−15)2+⋯+(x20−15)2] 中，可以看出15表示这组数据的 ．

    查看试题解析

三、解答题

  • 16.

    2009年5月31日，A、B两地的气温变化如下图所示：

    （1）这一天A地气温的极差是?B地气温的极差是?

    （2）A、B两地气候有什么异同？

    查看试题解析

  • 17.

    下图为小亮家09年月用电量的统计图，请根据统计图回答问题．

    （1）若小亮家一年用电总量为1 080千瓦时，则11月份的用电量为多少千瓦时；并补全该统计图；

    （2）小亮家该年月用电量的极差是多少千瓦时；

    （3）为鼓励居民节约用电，小亮家所在地按下表规定收取电费：

     每户每月用电量

    不超过80千瓦时

     超过80千瓦时的部分

     电费单价（元/千瓦时）

                a

                   b

    如果小亮家3、4、5月份的电费分别是43.2元、36元、27元．求出a、b的值，并计算小亮家该年应交的电费总额．

    查看试题解析

  • 18. 某校开展一项以班级为单位的投三分球比赛．规则如下：①在三分投篮线外，将球投向筐中，只要投进一次，该局便结束；②若一次未进可再投第二次，以此类推，直至投进；③若投第n次时才投中，则得分为n；④每班安排5位选手，5人得分之和为该班最终积分，积分最小的班级获胜．为确定参加比赛的人选，初三（1）班组织本班体育爱好者进行了预选赛，有4名同学成绩非常突出，已被确定为参赛选手，班主任通过统计分析，准备从双胞胎兄弟姚亦、姚新两人中挑选一人为最后一位选手，他俩的比赛得分如下：

    姚亦：3，1，5，4，3，2，3，6，8，5；

    姚新：1，4，3，3，1，3，2，8，3，12．

    （1）姚亦、姚新兄弟俩的平均得分分别是多少？

    （2）姚亦得分的中位数、众数、极差分别是多少？

    （3）利用你所学习到的统计知识，请你帮助班主任确定最后一位选手，并说明理由．

    查看试题解析

四、综合题

  • 19. 某校为了解七、八年级学生英语听力训练情况（七、八年级学生人数相同），某周从这两个年级学生中分别随机抽查了30名同学，调查了他们周一至周五的听力训练情况，根据调查情况得到如下统计图表：周一至周五英语听力训练人数统计表

    年级

    参加英语听力训练人数

    周一

    周二

    周三

    周四

    周五

    七年级

    15

    20

    a

    30

    30

    八年级

    20

    24

    26

    30

    30

    合计

    35

    44

    51

    60

    60

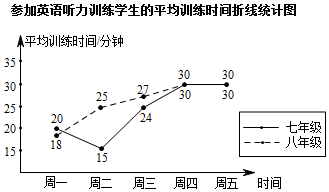    (1)、填空： a = ；
    (2)、根据上述统计图表完成下表中的相关统计量：

    年级

    平均训练时间的中位数

    参加英语听力训练人数的方差

    七年级

    24

    34

    八年级

    		  

    14.4
    (3)、请你利用上述统计图表，对七、八年级英语听力训练情况写出两条合理的评价；
    (4)、请你结合周一至周五英语听力训练人数统计表，估计该校七、八年级共480名学生中周一至周五平均每天有多少人进行英语听力训练.

    查看试题解析

  • 20. 小聪、小明准备代表班级参加学校“团史知识”竞赛，班主任对这两名同学测试了6次，获得如图测试成绩折线统计图．根据图中信息，解答下列问题：

     

    (1)、根据上面的折线统计图，补全下列表格中的统计量：

    学生

    平均数

    中位数

    众数

    极差

    方差

    小聪

    8

    b

    c

    3

    f

    小明

    a

    8

    d

    e

    3

    a= ， b= ， c= ， d= ， e= ， f= ．

    (2)、只结合小聪和小明成绩的平均数、中位数，的数学成绩较好；只结合小聪和小明成绩的极差和方差，的数学成绩较稳定．

    查看试题解析

  • 21. 省射击队为从甲、乙两名运动员中选拔一人参加全国比赛，对他们进行了六次测试，测试成绩如下表（单位：环）：


    第一次

    第二次

    第三次

    第四次

    第五次

    第六次

    甲

    10

    8

    9

    8

    10

    9

    乙

    10

    7

    10

    10

    9

    8

    (1)、根据表格中的数据，计算出甲的平均成绩是环，乙的平均成绩是环；
    (2)、分别计算甲、乙六次测试成绩的方差；你认为推荐谁参加全国比赛更合适，请说明理由．

    查看试题解析

  • 22. 2021年4月13日，日本政府召开内阁会议正式决定，将福岛第一核电站超过100万公吨的核污水经过滤并稀释后排入大海，这一决定遭到包括福岛民众、日本渔民乃至国际社会的谴责和质疑．鉴于此次事件的恶劣影响，某校为了强化学生的环保意识，校团委在全校举办了“保护环境，人人有责”知识竞赛活动，初、高中根据初赛成绩，各选出5名选手组成初中代表队和高中代表队进行复赛，复赛成绩如图所示．

    根据以上信息解答下列问题：

    (1)、高中代表队五名学生复赛成绩的中位数为分；
    (2)、分别计算初中代表队、高中代表队学生复赛成绩的平均数；
    (3)、已知高中代表队学生复赛成绩的方差为20，请计算初中代表队学生复赛成绩的方差，并结合两队成绩的平均数和方差分析哪个队的复赛成绩较好．

    查看试题解析

  • 23. 小聪、小明准备代表班级参加学校“党史知识”竞赛，班主任对这两名同学测试了6次，获得如下测试成绩折线统计图．根据图中信息，解答下列问题：

    (1)、要评价每位同学成绩的平均水平，你选择什么统计量？求这个统计量．
    (2)、求小聪成绩的方差．
    (3)、现求得小明成绩的方差为 S小明2=3 （单位：平方分）．根据折线统计图及上面两小题的计算，你认为哪位同学的成绩较好？请简述理由．

    查看试题解析