（鲁教版）2022-2023学年度第一学期八年级数学3.3从统计图分析数据的集中趋势 同步测试
试卷更新日期：2022-10-25 类型：同步测试
一、单选题
-
1. 某校随机抽查了10名学生的体育成绩，得到的结果如表：
成绩（分）
46
47
48
49
50
人数（人）
1
2
3
2
2
下列说法正确的是（ ）
A、这10名同学的体育成绩的方差为50 B、这10名同学的体育成绩的众数为50分 C、这10名同学的体育成绩的中位数为48分 D、这10名同学的体育成绩的平均数为48分2. 5月1日至7日，我市每日最高气温如图所示，则下列说法错误的是（ ）
A、中位数是 B、众数是 C、平均数是 D、4日至5日最高气温下降幅度较大3. 对于一列数据(数据个数不少于6），如果去掉一个最大值和一个最小值，那么这列数据分析一定不受影响的是（ ）A、平均数 B、中位数 C、众数 D、方差4. 某校九（1）班语文课代表统计了去年1～8月“我爱读书”活动中全班同学的课外阅读数量（单位：本），绘制了如图折线统计图，在这组课外阅读数量的数据中，中位数和众数分别是（ ）
A、53，56 B、53，63 C、56，56 D、56，635. 小明同学对数据15，28，36，4□，43进行统计分析，发现其中一个两位数的个位数字被黑水涂污看不到了，则统计结果与被涂污数字无关的是（ ）A、平均数 B、标准差 C、中位数 D、极差6. 在第十四届全运会女排比赛中，山东女子排球队6名场上队员的身高（单位：cm）是：180，184，188，190，192，194．现用一名身高为186cm的队员换下场上身高为192cm的队员，与换人前相比，场上队员的身高（ ）A、平均数变小，极差变大 B、中位数变小，方差变小 C、平均数变大，极差变小 D、中位数变大，方差变大7. 某次知识竞赛中，10名学生的成绩统计如下：分数(分)
60
70
80
90
100
人数(人)
1
1
5
2
1
则下列说明正确的是（ ）
A、学生成绩的极差是4 B、学生成绩的众数是5 C、学生成绩的中位数是80分 D、学生成绩的平均分是80分8. 下列说法错误的是（ ）A、平均数受极端值的影响比较大 B、极差是一组数据中最大的数与最小的数的差 C、一组数据的众数一定只有一个 D、方差能反映一组数据的波动程度9. 某品牌皮鞋店销售同种品牌不同尺码的男鞋，采购员再次进货时，对于男鞋的尺码，他最关注下列统计资料中的（ ）A、众数 B、中位数 C、加权平均数 D、平均数10. 为筹备班级元旦联欢会，班长对全班同学爱吃哪几种水果做了民意调查，然后决定买什么水果，最值得关注的应该是统计调查数据的（ ）A、方差 B、中位数 C、平均数 D、众数二、填空题
-
11. 据统计，近几年全世界森林面积以每年约1700万公顷的速度消失，为了预测未来20年世界森林面积的变化趋势，可选用统计图表示收集到的数据．12. 气象部门为了了解3月份气温的变化趋势，最好选用的统计图是 ．13. 王胖子在扬州某小区经营特色长鱼面，生意火爆，开业前5天销售情况如下：第一天46碗，第二天54碗，第三天69碗，第四天62碗，第五天87碗，如果要清楚地反映王胖子的特色长鱼面在前5天的销售情况，不能选择统计图．
14. 学校举行“纪念反法西斯战争胜利70周年”演讲比赛，共有15名同学进入决赛，比赛将评出金奖1名，银奖3名，铜奖4名．某参赛选手知道自己的分数后，要判断自己能否获奖，他应该关注的是有关成绩的 ． （填“平均数”、“中位数”或“众数”）15. 学校要从小明等13名同学出选出6名学生参加数学竞赛．经过选拔赛后，小明想提前知道自己能否被选上，他除了要知道自己的成绩以外，还要知道这13名同学成绩的 ．三、解答题
-
16. 某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡，根据它们的质量（单位： ），绘制出如下的统计图①和图②.请根据相关信息，解答下列问题：
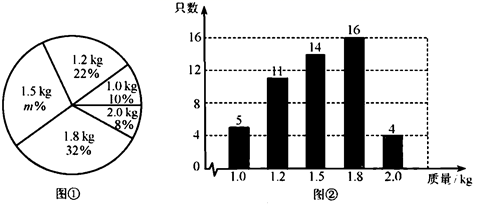
（Ⅰ）图①中 的值为_▲__；
（Ⅱ）求统计的这组数据的平均数、众数和中位数；
（Ⅲ） 根据样本数据，估计这2500只鸡中，质量为 的约有多少只？
17.柴静自费力作《穹顶之下》关于雾霾的深度调查中，提到2014雾霾天超过200天的城市，让人难以想象的是杭州竟然位列其中．据调查造成杭州雾霾严重的主要原因是汽车尾气的排放，它占到PM2.5来源的40%，下面是近几年杭州汽车保有量的统计图，请指出：
（1）哪一年汽车增长的速度最快．
（2）请计算2013年汽车的年增长率，2014年杭州限牌后增长速度有所缓解，如果没有限牌，继续按着03年的增长率继续增长（以后每年的增长率相同）预计2014年汽车保有量达到多少，2016年呢？（精确到个位）
（3）请对改善杭州的环境提出一个有效的建议．
18.某实验校七、八、九三个年级的同学参加了今年植树活动，下面的象形图描述了该三个年级的植树情况，根据这一象形图解答：
（1）这三个年级今年共植树多少棵？
（2）请将这个象形图所表过的信息改用条形图表达．
（3）用扇形图表达三个年级植树所占比例情况．
19. 三五三七鞋厂为了了解初中学生穿鞋的鞋号情况，对红华中学初二（1）班的20名男生所穿鞋号统计如下表：鞋号
23.5
24
24.5
25
25.5
26
人数
3
4
4
7
1
1
（1）写出男生鞋号数据的平均数，中位数，众数；
（2）在平均数，中位数和众数中，鞋厂最感兴趣的是什么？
20. 你的母亲开了一家服装店，专门卖羽绒服，下面是去年一年各月销售情况表：月份
1
2
3
4
5
6
7
8
9
10
11
12
销量（件）
100
90
50
11
8
6
4
6
5
30
80
110
根据表，回答下列问题：
（1）计算去年各季度的销售情况，并用一个适当的统计图表示；
（2）计算去年各季度销售量在全年销售总量中所占的百分比，并用适当统计图表示；
（3）从这些统计图表中，你能得出什么结论为你母亲今后决策能提供什么有用帮助．
四、综合题
-
21. 为了加强安全教育，我校组织八、九年级开展了以“烤火必开窗，关窗先灭火”为主题知识竞赛，为了解竞赛情况，从两个年级各随机抽取了20名同学的成绩（满分为100分）.收集整理数据如表：
分数
70
75
80
85
90
95
100
八年级
2人
3人
2人
4人
5人
3人
1人
九年级
0人
2人
5人
8人
2人
a人
1人
分析数据：
平均数
中位数
众数
方差
八年级
b
c
90
76.3
九年级
85
85
d
42.1
根据以上信息回答下列问题：
(1)、a＝ ， b＝ ， c＝ ， d＝；(2)、请通过平均数和方差分析两个年级掌握防火知识的情况；(3)、该校八、九年级共有1000人，本次知识竞赛成绩不低于85分的为“优秀”.请估计这两个年级共有多少名学生到达“优秀”.22. “双减”政策实施以来，我校积极探寻更为合理的学生评价方案.班主任石老师对班级学生的学习生活等采取的是量化积分制.下面统计的是博学组和笃行组连续八周的量化积分，并将得到的数据制成如下的统计表：量化积分统计表（单位：分）
周次
组别
一
二
三
四
五
六
七
八
博学组
12
14
16
14
14
13
15
14
笃行组
13
11
15
17
16
18
13
9
(1)、请根据表中的数据完成下表平均数
中位数
众数
方差
博学组
14
14
笃行组
14
8.25
(2)、根据量化积分统计表中的数据，请在下图中画出笃行组量化积分的折线统计图.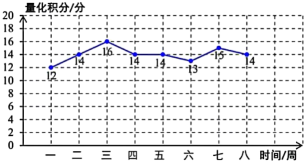
(3)、根据折线统计图中的信息，请你对这两个小组连续八周的学习生活情况作出一条简要评价.23. 深圳市教育局印发的《深圳市义务教育阶段学校课后服务实施意见》明确中小学课后延时服务从2021年3月5日开始实施某校积极开展课后延时服务活动，提供了“有趣的生物实验、经典影视欣赏、虚拟机器人竞赛、趣味篮球训练、国际象棋大赛……”等课程供学生自由选择．一个学期后，该校现为了解学生对课后延时服务的满意情况，随机对部分学生进行问卷调查，并将调查结果按照“A．非常满意；B．比较满意；C．基本满意；D．不满意”四个等级绘制成了如图所示的两幅不完整的统计图：
请你根据图中信息，解答下列问题：
(1)、该校抽样调查的学生人数为人，请补全条形统计图；(2)、样本中，学生对课后延时服务满意情况的“中位数”所在等级为 ， “众数”所在等级为；（填“A、B、C或D”）(3)、若该校共有学生2100人，据此调查估计全校学生对延时服务满意（包含A、B、C三个等级）的学生有人．