(鲁教版)2022-2023学年度第一学期九年级数学3.1对函数的再认识 同步测试
试卷更新日期:2022-10-25 类型:同步测试
一、单选题
-
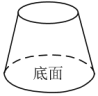
1. 如图所示,有一个容器水平放置,往此容器内注水,注满为止.若用h(单位:cm)表示容器底面到水面的高度,用V(单位:)表示注入容器内的水量,则表示V与h的函数关系的图象大致是( )
 A、
A、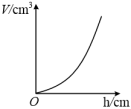 B、
B、 C、
C、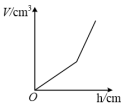 D、
D、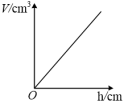 2. 如图,线段AB=5,动点P以每秒1个单位长度的速度从点A出发,沿线段AB运动至点B,以点A为圆心,线段AP长为半径作圆.设点P的运动时间为t,点P,B之间的距离为y,⊙A的面积为S,则y与t,S与t满足的函数关系分别是( )
2. 如图,线段AB=5,动点P以每秒1个单位长度的速度从点A出发,沿线段AB运动至点B,以点A为圆心,线段AP长为半径作圆.设点P的运动时间为t,点P,B之间的距离为y,⊙A的面积为S,则y与t,S与t满足的函数关系分别是( ) A、正比例函数关系,一次函数关系 B、一次函数关系,正比例函数关系 C、一次函数关系, 二次函数关系 D、正比例函数关系,二次函数关系3. 如图,矩形纸片ABCD中,BC=4,AB=3,点P是BC边上的动点(点P不与点B、C重合).现将△PCD沿PD翻折,得到△PC′D , 作∠BPC′的角平分线,交AB于点E . 设BP=x , BE=y , 则下列图象中,能表示y与x的函数关系的图象大致是( )
A、正比例函数关系,一次函数关系 B、一次函数关系,正比例函数关系 C、一次函数关系, 二次函数关系 D、正比例函数关系,二次函数关系3. 如图,矩形纸片ABCD中,BC=4,AB=3,点P是BC边上的动点(点P不与点B、C重合).现将△PCD沿PD翻折,得到△PC′D , 作∠BPC′的角平分线,交AB于点E . 设BP=x , BE=y , 则下列图象中,能表示y与x的函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、 4. 如图,有一个球形容器,小海在往容器里注水的过程中发现,水面的高度h、水面的面积S及注水量V是三个变量.下列有四种说法:①S是V的函数;②V是S的函数;③h是S的函数;④S是h的函数.其中所有正确结论的序号是( )
4. 如图,有一个球形容器,小海在往容器里注水的过程中发现,水面的高度h、水面的面积S及注水量V是三个变量.下列有四种说法:①S是V的函数;②V是S的函数;③h是S的函数;④S是h的函数.其中所有正确结论的序号是( )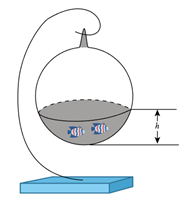 A、①③ B、①④ C、②③ D、②④5. 下列曲线中,表示y是x的函数的是 ( )A、
A、①③ B、①④ C、②③ D、②④5. 下列曲线中,表示y是x的函数的是 ( )A、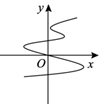 B、
B、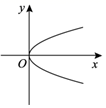 C、
C、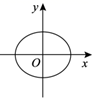 D、
D、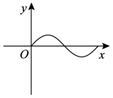 6. 某班“数学兴趣小组”探究出了有关函数 (图象如图)的三个结论:①方程 有1个实数根,该方程的根是 ;②如果方程 只有一个实数根,则a的取值范围是 或 ;③如果方程 有2个实数根,则a的取值范围是 或 .你认为正确的结论个数有( )
6. 某班“数学兴趣小组”探究出了有关函数 (图象如图)的三个结论:①方程 有1个实数根,该方程的根是 ;②如果方程 只有一个实数根,则a的取值范围是 或 ;③如果方程 有2个实数根,则a的取值范围是 或 .你认为正确的结论个数有( ) A、3 B、2 C、1 D、07. 向下图所示的空水壶内匀速注水,则下列描述壶内水的深度h (单位:cm)与注水时间t (单位:秒)关系的函数图象中,正确的是( )
A、3 B、2 C、1 D、07. 向下图所示的空水壶内匀速注水,则下列描述壶内水的深度h (单位:cm)与注水时间t (单位:秒)关系的函数图象中,正确的是( ) A、
A、 B、
B、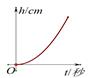 C、
C、 D、
D、 8. 下列解析式中,y不是x的函数的是( ).A、 B、 C、 D、9. 在平面直角坐标系 中,下列函数的图象上存在点 的是( )A、 B、 C、 D、10. 如图,菱形 对角线 , 相交于点 ,点 , 分别在线段 , 上,且 .以 为边作一个菱形,使得它的两条对角线分别在线段 , 上,设 ,新作菱形的面积为 ,则反映 与 之间函数关系的图象大致是( )
8. 下列解析式中,y不是x的函数的是( ).A、 B、 C、 D、9. 在平面直角坐标系 中,下列函数的图象上存在点 的是( )A、 B、 C、 D、10. 如图,菱形 对角线 , 相交于点 ,点 , 分别在线段 , 上,且 .以 为边作一个菱形,使得它的两条对角线分别在线段 , 上,设 ,新作菱形的面积为 ,则反映 与 之间函数关系的图象大致是( ) A、
A、 B、
B、 C、
C、 D、
D、
二、填空题
-
11. 我们把 三个数的中位数记作 ,直线 与函数 的图象有且只有2个交点,则k的取值为12. 对于实数a,b定义运算“*”:a*b=a2-ab(a≤b),a*b=b2-ab(a>b),关于x的方程(2x-1) * (x-1) =m恰有三个不相等的实数根,则m的取值范围13. 暑假假期,小明和小亮两家相约自驾车从重庆出发前往相距172千米的景区游玩两家人同时同地出发,以各自的速度匀速行驶,出发一段时间后,小明家因故停下来休息了15分钟,为了尽快追上小亮家,小明家提高速度后仍保持匀速行驶(加速的时间忽略不计),小明家追上小亮家后以提高后的速度直到景区,小亮家保持原速,如图是小明家、小亮家两车之间的距离s(km)与出发时间t(h)之间的函数关系图象,则小明家比小亮家早到景区分钟.
 14. 已知甲、乙两车分别从A、B两地同时出发,以各自的速度匀速相向而行,两车相遇后,乙车继续向终点A地行使,而甲车原地停留了一段时间后才继续驶向终点B地,两车到达各自的终点后分别停止运动.若整个过程中,甲、乙两车各自的速度均保持不变,且甲、乙两车之间的距离s(千米)与乙车行驶时间t(小时)的函数图象如图所示,则甲车比乙车早到小时.
14. 已知甲、乙两车分别从A、B两地同时出发,以各自的速度匀速相向而行,两车相遇后,乙车继续向终点A地行使,而甲车原地停留了一段时间后才继续驶向终点B地,两车到达各自的终点后分别停止运动.若整个过程中,甲、乙两车各自的速度均保持不变,且甲、乙两车之间的距离s(千米)与乙车行驶时间t(小时)的函数图象如图所示,则甲车比乙车早到小时.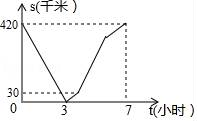 15. 知函数 使y=a成立的x的值恰好只有2个时,则a满足的条件是.
15. 知函数 使y=a成立的x的值恰好只有2个时,则a满足的条件是.
三、解答题
-
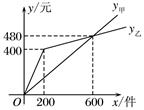
16. 某厂家在甲、乙两家商场销售同一种商品所获得的利润分别为y甲 , y乙(单位:元),y甲 , y乙与销售数量x(单位:件)的函数关系如图所示,请根据图象分别求出y甲 , y乙关于x的函数解析式.
 17. 已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.
17. 已知y是x的函数,自变量x的取值范围是x>0,下表是y与x的几组对应值.x
…
1
2
4
5
6
8
9
…
y
…
3.92
1.95
0.98
0.78
2.44
2.44
0.78
…
小风根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象和性质进行了探究.
下面是小风的探究过程,请补充完整:
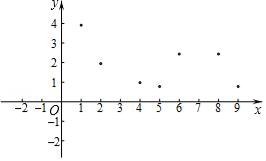
(1)、如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;(2)、根据画出的函数图象,写出:①x=7对应的函数值y约为多少;
②写出该函数的一条性质.
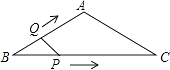
 18. 如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以 cm/s的速度沿BC方向
18. 如图,在等腰△ABC中,AB=AC=4cm,∠B=30°,点P从点B出发,以 cm/s的速度沿BC方向运动到点C停止,同时点Q从点B出发,以1cm/s的速度沿BA-AC方向运动到点C停止,若△BPQ的面积为y(cm2),运动时间为x(s),求在这一运动过程中y与x之间函数关系式.
 19. 某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.
19. 某天早晨,王老师从家出发,骑摩托车前往学校,途中在路旁一家饭店吃早餐,如图所示的是王老师从家到学校这一过程中行驶路程s(千米)与时间t(分)之间的关系.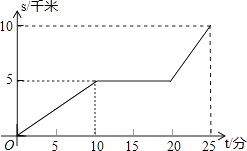 (1)、学校离他家多远?从出发到学校,用了多少时间?(2)、王老师吃早餐用了多少时间?(3)、王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?20. 某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题:
(1)、学校离他家多远?从出发到学校,用了多少时间?(2)、王老师吃早餐用了多少时间?(3)、王老师吃早餐以前的速度快还是吃完早餐以后的速度快?最快时速达到多少?20. 某旅游团上午6时从旅馆出发,乘汽车到距离210km的某著名旅游景点游玩,该汽车离旅馆的距离S(km)与时间t(h)的关系可以用如图的折线表示.根据图象提供的有关信息,解答下列问题: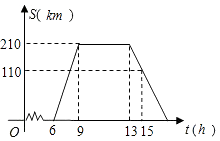 (1)、求该团去景点时的平均速度是多少?(2)、该团在旅游景点游玩了多少小时?(3)、求返回到宾馆的时刻是几时几分?21. 一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.
(1)、求该团去景点时的平均速度是多少?(2)、该团在旅游景点游玩了多少小时?(3)、求返回到宾馆的时刻是几时几分?21. 一个装有进水管和出水管的容器,从某时刻开始的4分钟内只进水不出水,在随后的8分钟内既进水又出水,接着关闭进水管直到容器内的水放完.假设每分钟的进水量和出水量是两个常数,容器内的水量y(单位:升)与时间x(单位:分钟)之间的部分关系如图象所示.求从关闭进水管起需要多少分钟该容器内的水恰好放完.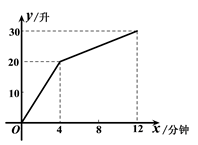 22. 某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示:根据图象解答下列问题:
22. 某洗衣机在洗涤衣服时,经历了进水、清洗、排水、脱水四个连续过程,其中进水、清洗、排水时洗衣机中的水量y(升)与时间x(分钟)之间的关系如折线图所示:根据图象解答下列问题: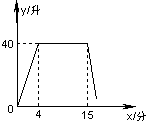 (1)、洗衣机的进水时间是分钟;清洗时洗衣机中的水量是升;(2)、已知洗衣机的排水速度为每分钟19升,
(1)、洗衣机的进水时间是分钟;清洗时洗衣机中的水量是升;(2)、已知洗衣机的排水速度为每分钟19升,①求排水时y与x之间的关系式.
②如果排水时间为2分钟,求排水结束时洗衣机中剩下的水量.
23. 钓鱼岛自古就是中国领土,中国政府已对钓鱼岛开展常态化巡逻.某人,为按计划准点到达指定海拔,某巡逻艇凌晨1:00出发,匀速行驶一段时间后,因中途出现故障耽搁了一段时间,故障排除后,该艇加快速度仍匀速前进,结果恰好准点到达.如图是该艇行驶的路程y(海里)与所用时间t(小时)的函数图象,求该巡逻艇原计划准点到的时间.