(苏科版)2022-2023学年九年级数学下册第六章 图形的相似 同步测试
试卷更新日期:2022-10-25 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 若3x=4y,则下列结论一定成立的是( )A、 = B、 = C、 = D、 =2. 如图所示,以长为2的线段AB为边作正方形ABCD,取AB的中点P,连接PD,在BA的延长线上取点F,使PF=PD,以AF为边作正方形AMEF,点M在AD上,则AM的长为( )
 A、 ﹣1 B、 C、3﹣ D、6﹣23. 若3a=4b,则(a﹣b):(a+b)的值是( )A、 B、7 C、﹣ D、﹣74. 已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积比为( )A、4:3 B、3:4 C、16:9 D、9:165. 如图,四个全等的直角三角形拼成“赵爽弦图”得到正方形ABCD与正方形EFGH.连接EG,BD相交于点O,BD与HC相交于点P.若GO=GP,下列结论:①∠GOP=∠BCP,②BC=BP,③BG:PG= +1,④DP=PO.正确的是( )
A、 ﹣1 B、 C、3﹣ D、6﹣23. 若3a=4b,则(a﹣b):(a+b)的值是( )A、 B、7 C、﹣ D、﹣74. 已知△ABC∽△DEF,若△ABC与△DEF的相似比为3:4,则△ABC与△DEF的面积比为( )A、4:3 B、3:4 C、16:9 D、9:165. 如图,四个全等的直角三角形拼成“赵爽弦图”得到正方形ABCD与正方形EFGH.连接EG,BD相交于点O,BD与HC相交于点P.若GO=GP,下列结论:①∠GOP=∠BCP,②BC=BP,③BG:PG= +1,④DP=PO.正确的是( ) A、②③④ B、①③④ C、①②④ D、①②③6. 如图,在 中,如果点 是边 的中点,且 ,那么下列结论错误的是( )
A、②③④ B、①③④ C、①②④ D、①②③6. 如图,在 中,如果点 是边 的中点,且 ,那么下列结论错误的是( )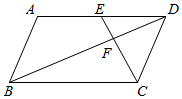 A、 B、 C、 D、7. 如图,在 中,已知 ,E,F分别在边AC,AB上,DE//BC,DF//AC,则( )
A、 B、 C、 D、7. 如图,在 中,已知 ,E,F分别在边AC,AB上,DE//BC,DF//AC,则( ) A、 B、 C、 D、8. 如图,已知△ACD∽△ADB,AC=4,AD=2,则AB的长为( )
A、 B、 C、 D、8. 如图,已知△ACD∽△ADB,AC=4,AD=2,则AB的长为( ) A、1 B、2 C、3 D、49. 如图,△ABC中,顶点A、B均在第二象限,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C',且△A'B'C'与△ABC的位似比为2:1,设点B的对应点B'的横坐标是3,则点B的横坐标是( )
A、1 B、2 C、3 D、49. 如图,△ABC中,顶点A、B均在第二象限,点C的坐标是(﹣1,0),以点C为位似中心,在x轴的下方作△ABC的位似图形△A'B'C',且△A'B'C'与△ABC的位似比为2:1,设点B的对应点B'的横坐标是3,则点B的横坐标是( )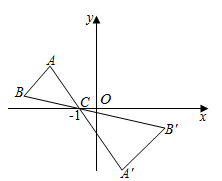 A、 B、﹣2 C、 D、﹣310.
A、 B、﹣2 C、 D、﹣310.现有一张Rt△ABC纸片,直角边BC长为l2cm,另一直角边AB长为24cm.现沿BC边依次从下往上裁剪宽度均为3cm的矩形纸条,如图.已知剪得的纸条中有一张是正方形,则这张正方形纸条是( )
 A、第4张 B、第5张 C、第6张 D、第7张
A、第4张 B、第5张 C、第6张 D、第7张二、填空题(每题3分,共15分)
-
11. 已知 ,则 =.12. P为线段AB的黄金分割点,AP>BP,如果AP=10cm,那么BP=cm.(精确到0.1cm)13. 在一张比例尺为1︰50000的地图中,小明家到动车站的距离有0.2米,则小明家到动车站的实际距离是 米.14. 如图中两三角形相似,则x= .
 15. 如图,在直角坐标系中,△ABC的各顶点坐标为A(﹣1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为 .则点A的对应点A′的坐标为 .
15. 如图,在直角坐标系中,△ABC的各顶点坐标为A(﹣1,1),B(2,3),C(0,3).现以坐标原点为位似中心,作△A′B′C′,使△A′B′C′与△ABC的位似比为 .则点A的对应点A′的坐标为 .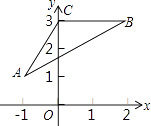
三、解答题(共8题,共55分)
-
16. 阅读下列解题过程,然后解题:
题目:已知 互不相等),求 的值.
解:设 ,则 , ,
, .
依照上述方法解答下列问题:
已知 ,其中 ,求 的值.
17. 五角星是我们常见的图形,如图所示,其中,点C,D分别是线段AB的黄金分割点,AB=20cm,求EC+CD的长. 18. 阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”:如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题:
18. 阅读理解:如图1,在四边形ABCD的边AB上任取一点E(点E不与A、B重合),分别连接ED、EC,可以把四边形ABCD分成三个三角形,如果其中有两个三角形相似,我们就把E叫做四边形ABCD的边AB上的“相似点”:如果这三个三角形都相似,我们就把E叫做四边形ABCD的边AB上的“强相似点”.解决问题:(1)如图1,∠A=∠B=∠DEC=45°,试判断点E是否是四边形ABCD的边AB上的相似点,并说明理由;
(2)如图2,在矩形ABCD中,A、B、C、D四点均在正方形网格(网格中每个小正方形的边长为1)的格点(即每个小正方形的顶点)上,试在图②中画出矩形ABCD的边AB上的强相似点;
(3)如图3,将矩形ABCD沿CM折叠,使点D落在AB边上的点E处,若点E恰好是四边形ABCM的边AB上的一个强相似点,试探究AB与BC的数量关系.
 19. 如图,已知菱形BEDF,内接于△ABC,点E,D,F分别在AB,AC和BC上.若AB=15cm,BC=12cm,求菱形边长.
19. 如图,已知菱形BEDF,内接于△ABC,点E,D,F分别在AB,AC和BC上.若AB=15cm,BC=12cm,求菱形边长.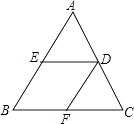 20. 已知矩形OABC的顶点O(0,0)、A(4,0)、B(4,-3).动点P从O出发,以每秒1个单位的速度,沿射线OB方向运动.设运动时间为t秒.
20. 已知矩形OABC的顶点O(0,0)、A(4,0)、B(4,-3).动点P从O出发,以每秒1个单位的速度,沿射线OB方向运动.设运动时间为t秒.
(1)求P点的坐标(用含t的代数式表示);
(2)如图,以P为一顶点的正方形PQMN的边长为2,且边PQ⊥y轴.设正方形PQMN与矩形OABC的公共部分面积为S,当正方形PQMN与矩形OABC无公共部分时,运动停止.
①当t<4时,求S与t之间的函数关系式;
②当t>4时,设直线MQ、MN分别交矩形OABC的边BC、AB于D、E,问:是否存在这样的t,使得△PDE为直角三角形?若存在,请求出所有符合条件的t的值;若不存在,请说明理由. 21. 如图,在边长为1的正方形网格内有一个三角形ABC
21. 如图,在边长为1的正方形网格内有一个三角形ABC
(1)把△ABC沿着轴向右平移5个单位得到△A1B1C1 , 请你画出△A1B1C1
(2)请你以O点为位似中心在第一象限内画出△ABC的位似图形△A2B2C2 , 使得△ABC与△A2B2C2的位似比为1:2;
(3)请你写出△A2B2C2三个顶点的坐标。(3分)
22. 一天晚上,李明和张龙利用灯光下的影子来测量一路灯D的高度,如图,当李明走到点A处时,张龙测得李明直立时身高AM与影长AE正好相等,接着李明沿AC方向继续向前走,走到点B处时,李明直立时身高BN的影子恰好是线段AB,并测得AB=1.25 m.已知李明直立时的身高为1.75 m,求路灯的高CD的长.(结果精确到0.1 m) 23. 如图,△ABC中,∠C=90°,AC=3,BC=4,在线段AB上,动点M从点A出发向点B做匀速运动,同时动点N从B出发向点A做匀速运动,当点M、N其中一点停止运动时,另一点也停止运动,分别过点M、N作AB的垂线,分别交两直角边AC,BC所在的直线于点D、E,连接DE,若运动时间为t秒,在运动过程中四边形DENM总为矩形(点M、N重合除外).
23. 如图,△ABC中,∠C=90°,AC=3,BC=4,在线段AB上,动点M从点A出发向点B做匀速运动,同时动点N从B出发向点A做匀速运动,当点M、N其中一点停止运动时,另一点也停止运动,分别过点M、N作AB的垂线,分别交两直角边AC,BC所在的直线于点D、E,连接DE,若运动时间为t秒,在运动过程中四边形DENM总为矩形(点M、N重合除外).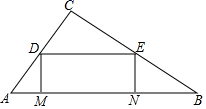 (1)、写出图中与△ABC相似的三角形;(2)、如图,设DM的长为x,矩形DENM面积为S,求S与x之间的函数关系式;当x为何值时,矩形DENM面积最大?最大面积是多少?(3)、在运动过程中,若点M的运动速度为每秒1个单位长度,求点N的运动速度.求t为多少秒时,矩形DEMN为正方形?
(1)、写出图中与△ABC相似的三角形;(2)、如图,设DM的长为x,矩形DENM面积为S,求S与x之间的函数关系式;当x为何值时,矩形DENM面积最大?最大面积是多少?(3)、在运动过程中,若点M的运动速度为每秒1个单位长度,求点N的运动速度.求t为多少秒时,矩形DEMN为正方形?