(苏科版)2022-2023学年九年级数学下册6.6 图形的位似 同步测试
试卷更新日期:2022-10-25 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图, 和 是以点 为位似中心的位似图形;若 ,则 和 的面积比为( )
 A、 B、 C、 D、2. 如图, 与 是以坐标原点O为位似中心的位似图形,若点A是 的中点, 的面积是6,则 的面积为( )
A、 B、 C、 D、2. 如图, 与 是以坐标原点O为位似中心的位似图形,若点A是 的中点, 的面积是6,则 的面积为( ) A、9 B、12 C、18 D、243. 如图,在平面直角坐标系中,每个小方格的边长均为1.△AOB与△ 是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是( )
A、9 B、12 C、18 D、243. 如图,在平面直角坐标系中,每个小方格的边长均为1.△AOB与△ 是以原点O为位似中心的位似图形,且相似比为3:2,点A,B都在格点上,则点B′的坐标是( ) A、(-2,1) B、(-2, ) C、(-2, ) D、(-2, )4. 下列各选项中的两个图形不是位似图形的是( )A、
A、(-2,1) B、(-2, ) C、(-2, ) D、(-2, )4. 下列各选项中的两个图形不是位似图形的是( )A、 B、
B、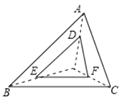 C、
C、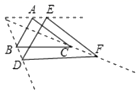 D、
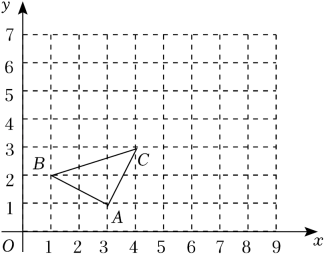
D、 5. 如图,若 与 是位似图形,则位似中心可能是( )
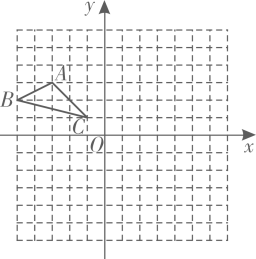
5. 如图,若 与 是位似图形,则位似中心可能是( ) A、 B、 C、 D、6. 如图,E(-4,2),F(-1,-1),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E`的坐标为( )
A、 B、 C、 D、6. 如图,E(-4,2),F(-1,-1),以O为位似中心,按比例尺1:2,把△EFO缩小,则点E的对应点E`的坐标为( )
 A、(2,-1)或(-2,1) B、(8,-4)或(-8,4) C、(2,-1) D、(8,4)7. 如图,已知 和 是位似图形,点O为位似中心.若 , 的面积为18,则 的面积为( )
A、(2,-1)或(-2,1) B、(8,-4)或(-8,4) C、(2,-1) D、(8,4)7. 如图,已知 和 是位似图形,点O为位似中心.若 , 的面积为18,则 的面积为( )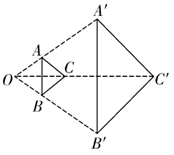 A、2 B、4 C、6 D、88. 如图,在平面直角坐标系中,以原点 为位似中心,在第一象限内,按照位似比 将 放大得到 ,且 点坐标为 , 点坐标为 ,则线段 长为( )
A、2 B、4 C、6 D、88. 如图,在平面直角坐标系中,以原点 为位似中心,在第一象限内,按照位似比 将 放大得到 ,且 点坐标为 , 点坐标为 ,则线段 长为( )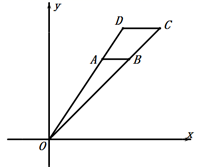 A、 B、2 C、 D、9. 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为P′( a+1, b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1 , △A′B′C′的面积为S2 , 则用等式表示S1与S2的关系为( )A、S1 S2 B、S1 S2 C、S1=2S2 D、S1=4S210. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的 ,那么点B'的坐标是( )
A、 B、2 C、 D、9. 平面直角坐标系xOy中,点P(a,b)经过某种变换后得到的对应点为P′( a+1, b﹣1).已知A,B,C是不共线的三个点,它们经过这种变换后,得到的对应点分别为A′,B′,C′.若△ABC的面积为S1 , △A′B′C′的面积为S2 , 则用等式表示S1与S2的关系为( )A、S1 S2 B、S1 S2 C、S1=2S2 D、S1=4S210. 如图,在直角坐标系中,矩形OABC的顶点O在坐标原点,边OA在x轴上,OC在y轴上,如果矩形OA'B'C'与矩形OABC关于点O位似,且矩形OA'B'C'的面积等于矩形OABC面积的 ,那么点B'的坐标是( )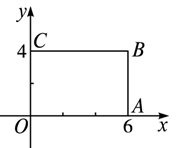 A、(3,2) B、(-2,-3) C、(2,3)或(-2,-3) D、(3,2)或(-3,-2)
A、(3,2) B、(-2,-3) C、(2,3)或(-2,-3) D、(3,2)或(-3,-2)二、填空题(每题3分,共15分)
-
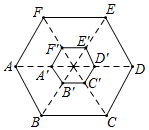
11. 如图,正六边形ABCDEF是由正六边形A′B′C′D′E′F′经过位似变换得到的,已知AB=3,B′C′=1,则正六边形A′B′C′D′E′F′和正六边形ABCDEF的面积比是 .
 12. 在平面直角坐标系中,△OAB各顶点的坐标分别为:O(0,0),A(1,2),B(0,3),以O为位似中心,△OA′B′与△OAB位似,若B点的对应点B′的坐标为(0,﹣6),则A点的对应点A′坐标为.13. 如图, 四边形OABC的顶点O为坐标原点,以O为位似中心,作出四边形OA1B1C1与四边形OABC位似,若A(6,0)的对应点为A1(4,0) ,四边形OABC的面积为27,则四边形OA1B1C1的面积为。
12. 在平面直角坐标系中,△OAB各顶点的坐标分别为:O(0,0),A(1,2),B(0,3),以O为位似中心,△OA′B′与△OAB位似,若B点的对应点B′的坐标为(0,﹣6),则A点的对应点A′坐标为.13. 如图, 四边形OABC的顶点O为坐标原点,以O为位似中心,作出四边形OA1B1C1与四边形OABC位似,若A(6,0)的对应点为A1(4,0) ,四边形OABC的面积为27,则四边形OA1B1C1的面积为。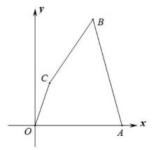 14. 如图,位似图形由三角尺与其灯光下的中心投影组成,相似比为2:5,且三角尺的一边长为8cm,则投影三角形的对应边长为㎝.
14. 如图,位似图形由三角尺与其灯光下的中心投影组成,相似比为2:5,且三角尺的一边长为8cm,则投影三角形的对应边长为㎝.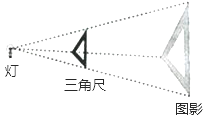 15. 如图,小“鱼”与大“鱼”是位似图形,如果小“鱼”上一个“顶点”的坐标为(a,﹣b),那么大“鱼”上对应“顶点”的坐标为 .
15. 如图,小“鱼”与大“鱼”是位似图形,如果小“鱼”上一个“顶点”的坐标为(a,﹣b),那么大“鱼”上对应“顶点”的坐标为 .
三、解答题(共8题,共55分)
-
16.
如图,在6×4的正方形方格中,△ABC的顶点A、B、C在单位正方形的格点上.
(1)请按要求画图:以点B为位似中心,在方格内将△ABC放大为原来的2倍,得到△EBD,且点D、E都在单位正方形的顶点上.
(2)在(1)中△ABC与△EBD的面积比是_____(直接写出答案)
 17.
17.如图所示,图中的小方格都是边长为1的正方形,△ABC与△A′B′C′是以点O为位似中心的位似图形,它们的顶点都在小正方形的顶点上.画出位似中心点O,并直接写出△ABC与△A′B′C′的位似比.
 18. 如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.
18. 如图,△ABC与△A′B′C′是位似图形,且顶点都在格点上,每个小正方形的边长都为1.

(1)在图上标出位似中心D的位置,并写出该位似中心D的坐标是 ;
(2)求△ABC与△A′B′C′的面积比.19.如图,△ABC在坐标平面内三个顶点的坐标分别为A(1,2)、B(3,3)、C(3,1).

(1)根据题意,请你在图中画出△ABC;
(2)在原图中,以B为位似中心,画出△A′BC′使它与△ABC位似且位似比是3:1,并写出顶点A′和C′的坐标.20. 如图,网格图的每个小正方形边长均为1.△OAB的顶点均在格点上.已知△与△OAB是以O为位似中心的位似图形,且位似比为1︰3.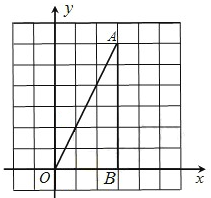
(1)请在第一象限内画出△;
(2)试求出△的面积.
21.已知△ABC在平面直角坐标系中的位置如图所示.

(1)将△ABC绕圆点O旋转180°得到△A1B1C1 , 请你在图中画出△A1B1C1;
(2)写出点A1的坐标;
(3)求△A1B1C1的面积.