（苏科版）2022-2023学年九年级数学下册6.5相似三角形的性质 同步测试
试卷更新日期：2022-10-25 类型：同步测试
一、单选题（每题3分，共30分）
-
1. 如图，△ABC的中线AD，BE交于点F，EG∥BC，交AD于点G，则GF：AG等于（ ）
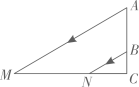
A、1：2 B、1：3 C、2：3 D、3：52. 若 且相似比为1：4，则 与 的面积比为（ ）A、1：4 B、4：1 C、1：16 D、16：13. 如图，已知△ABC∽△BDC，其中AC=4，CD=2，则BC=（ ）
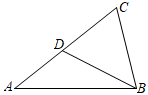A、2 B、 C、 D、44. 我国汉代数学家赵爽为了证明勾股定理，创制了一幅弦图，后人称其为赵爽弦图（如图1）.，图 2 为小明同学根据弦图思路设计的.在正方形 ABCD 中，以点 B 为圆心，AB 为半径作 AC，再 以CD 为直径作半圆交 AC 于点E，若边长AB=10，则△CDE 的面积为（ ）
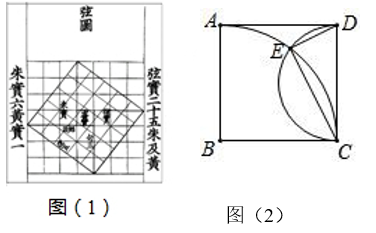A、20 B、 C、24 D、5. 如图，在平行四边形ABCD中，E为CD上一点，DE：CE＝2：3，连接AE，BD交于点F，则S△DEF：S△ADF：S△ABF等于（ ）
A、2：3：5 B、4：9：25 C、4：10：25 D、2：5：256. 如图，将菱形纸片ABCD折叠使点A恰好落在菱形的对称中心O处，折痕为EF，再次折叠图形，使点C恰好落在EF的中点G处，折痕为MN．若菱形ABCD的边长为2，∠A=120°，则MN的长度为（ ）
A、 B、2 C、 D、7. 如图，为了测量山坡护坡石坝的坡度（坡面的铅直高度与水平宽度的比称为坡度），把一根长 的竹竿 斜靠在石坝旁，量出杆长 处的 点离地面的高度 ，又量的杆底与坝脚的距离 ，则石坝的坡度为（ ）．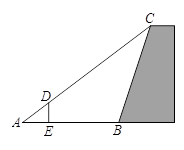
A、 B、 C、 D、8. 若△ABC∽△DEF，且△ABC与△DEF的面积比是 ，则△ABC与△DEF对应中线的比为（ ）A、 B、 C、 D、9. 若两个相似三角形的面积之比为1：2，则它们的周长之比为（ ）A、1：2 B、1：4 C、1：3 D、1：10. 若△ABC∽△A′B′C′，∠A=20°，∠C=120°，则∠B′的度数为（ ）A、20° B、30° C、40° D、120°二、填空题（每题3分，共15分）
-
11. 已知△ABC∽△DEF，相似比为3，则它们的周长之比是.12. △ABC中，AB＝8，AC＝6，点D在AC上且AD＝2，如果要在AB上找一点E，使△ADE与原三角形相似，那么AE＝13. 已知△ABC与△DEF的相似比为2∶3.若△ABC周长为12，则△DEF周长为.14. 已知两个相似三角形的面积比是4:1，则这两个三角形的周长比是.15. 如图， ，AD=10，BD=8， 与 相似，则CD=
三、解答题（共8题，共55分）
-
16. 如图，正方形ABCD的边长为2，AE=EB，MN=1，线段MN的两端在BC、CD上，若△ADE∽△CMN，求CM的长．
17. 如图，AB与CD相交于点O，△OBD∽△OAC， = ，OB=4，求AO和AB的长．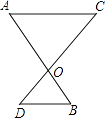
18.如图，在矩形ABCD中，AB=3cm，AD=4cm，点E是BC上一动点（不与B、C重合），且DF⊥AE，垂足为F. 设AE=xcm，DF=ycm.
（1）求证：△DFA∽△ABE；
（2）试求y与x之间的函数关系式，并求出自变量x的取值范围.19.已知，如图，过点E(0，-1)作平行于
轴的直线 ， 抛物线上的两点A、B的横坐标分别为
1和4，直线AB交y轴于点F，过点A、B分别作直线l的垂线，垂足分别为点C、D，连接CF，DF．
（1）求点A，B，F的坐标；
（2）求证：；
（3）点是抛物线对称轴右侧图象上的一动点，过点P作交X轴于点Q，是否存在点P使得与相似？若存在，请求出所有符合条件的点P的坐标；若不存在，请说明理由．20. 如图，在△ABC中，DE∥BC，AD：DB＝2：1，△ABC的面积为27，求△ADE的面积．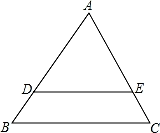
21. 如图，在△ABC中，AB＝10cm，BC＝20cm，点P从点A开始沿AB边向B点以2cm/s的速度移动，点Q从点B开始沿BC边向点C以4cm/s的速度移动，如果点P、Q分别从A、B同时出发，问经过几秒钟，△PBQ与△ABC相似．
