(苏科版)2022-2023学年九年级数学下册6.4探索相似三角形的条件 同步测试
试卷更新日期:2022-10-25 类型:同步测试
一、单选题
-
1. 如图,直线l1∥l2∥l3 , 直线AC分别交l1 , l2 , l3于点A,B,C,直线DF分别交l1 , l2 , l3于点D,E,F.若 ,则 的值为( )
 A、 B、 C、 D、2. 已知点A是双曲线在第一象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线上运动,则k的值是( )
A、 B、 C、 D、2. 已知点A是双曲线在第一象限分支上的一个动点,连接AO并延长交另一分支于点B,以AB为边作等边三角形ABC,点C在第四象限内,随着点A的运动,点C的位置也不断变化,但点C始终在双曲线上运动,则k的值是( ) A、1 B、 C、 D、23. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则 为( )
A、1 B、 C、 D、23. 如图,在Rt△ABC中,∠ACB=90°,以其三边为边向外作正方形,过点C作CI⊥HJ于点I,交AB于K,在图形的外部作矩形MNPQ,使点D,E,G和H,J都落在矩形的边上.已知矩形BJIK的面积为1,正方形ACDE的面积为4,则 为( ) A、 B、 C、 D、4. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=3:4,连接AE交对角线BD于点F,则S△DEF:S△ADF:S△ABF等于( )
A、 B、 C、 D、4. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=3:4,连接AE交对角线BD于点F,则S△DEF:S△ADF:S△ABF等于( ) A、3:4:7 B、9:16:49 C、9:21:49 D、3:7:495. 如图,在 ABCD中,E是AB边的中点,则 的值为( )
A、3:4:7 B、9:16:49 C、9:21:49 D、3:7:495. 如图,在 ABCD中,E是AB边的中点,则 的值为( ) A、 B、 C、 D、6. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连接AE,BD交于点F,则S∆DEF:S∆ADF:S∆ABF等于( )
A、 B、 C、 D、6. 如图,在平行四边形ABCD中,E为CD上一点,DE:CE=2:3,连接AE,BD交于点F,则S∆DEF:S∆ADF:S∆ABF等于( ) A、2:3:5 B、4:9:25 C、4:10:25 D、2:5:257. 如图,在△ABC中,∠ACB=90°,CD⊥AB,若AD=4,BD=8,则CD的长为( )
A、2:3:5 B、4:9:25 C、4:10:25 D、2:5:257. 如图,在△ABC中,∠ACB=90°,CD⊥AB,若AD=4,BD=8,则CD的长为( ) A、 B、4 C、 D、8. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=4:1,连接AE、BE,AE交BD于点F,则△BEC的面积与△BEF的面积之比为( )
A、 B、4 C、 D、8. 如图,在平行四边形ABCD中,点E在边DC上,DE:EC=4:1,连接AE、BE,AE交BD于点F,则△BEC的面积与△BEF的面积之比为( ) A、1:2 B、9:16 C、3:4 D、9:209. 如图,已知点G是ABC的重心,那么等于( )
A、1:2 B、9:16 C、3:4 D、9:209. 如图,已知点G是ABC的重心,那么等于( )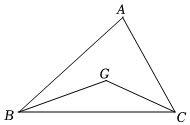 A、1:2 B、1:3 C、2:3 D、2:510. 如图,把 沿着 的方向平移到 的位置,它们重叠部分的面积是 面积的一半,若 ,则 移动的距离是( )
A、1:2 B、1:3 C、2:3 D、2:510. 如图,把 沿着 的方向平移到 的位置,它们重叠部分的面积是 面积的一半,若 ,则 移动的距离是( )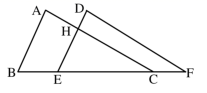 A、 B、 C、 D、
A、 B、 C、 D、二、解答题
-
11. 如图,在△ABC中,EFCD,DEBC.
 (1)、求证:AF:FD=AD:DB;(2)、若AB=30,AD:BD=2:1,请直接写出DF的长.12. 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5 ,求BD的长.
(1)、求证:AF:FD=AD:DB;(2)、若AB=30,AD:BD=2:1,请直接写出DF的长.12. 如图,在四边形ABCD中,∠ABC=90°,AB=3,BC=4,CD=10,DA=5 ,求BD的长. 13. 如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从B点开始沿边BC以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发,经过几秒钟后,以点P、B、Q三点为顶点的三角形与△ABC相似?
13. 如图,在△ABC中,AB=10cm,BC=20cm,点P从点A开始沿边AB向点B以2cm/s的速度移动,点Q从B点开始沿边BC以2cm/s的速度移动.如果点P,Q分别从点A,B同时出发,经过几秒钟后,以点P、B、Q三点为顶点的三角形与△ABC相似? 14. 在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示运动时间(0≤t≤6),那么当t为何值时,△APQ与△ABD相似?说明理由.
14. 在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/秒的速度移动,点Q沿DA边从点D开始向点A以1cm/秒的速度移动,如果P、Q同时出发,用t(秒)表示运动时间(0≤t≤6),那么当t为何值时,△APQ与△ABD相似?说明理由.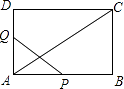 15. 如图,在中,的垂直平分线分别交 , 于点 , , 交于点 , .
15. 如图,在中,的垂直平分线分别交 , 于点 , , 交于点 , . (1)、求证:;(2)、求证:;(3)、的值等于.(直接写出结果,无需解答过程)16. 平面直角坐标系中,ΔABC的三个顶点坐标分别为A(1,-2),B(2,-1),C(4,-3) .
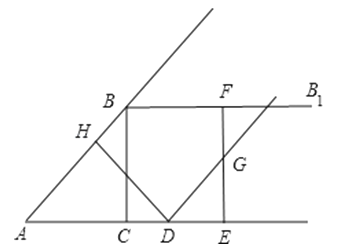
(1)、求证:;(2)、求证:;(3)、的值等于.(直接写出结果,无需解答过程)16. 平面直角坐标系中,ΔABC的三个顶点坐标分别为A(1,-2),B(2,-1),C(4,-3) .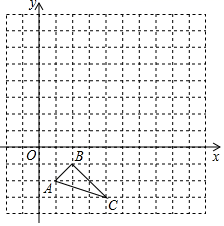 (1)、画出△A1B1C1 , 使它与△ABC关于x轴对称:(2)、以点(4,0)为位似中心,在网格中画出ΔABC的位似图形△A2B2C2 , 且△A2B2C2与△ABC的相似比为2:1;(3)、设点P(a,b)为△ABC内一点,则依上述变换后点P在△A2B2C2内的对应点P2的坐标是.17. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.
(1)、画出△A1B1C1 , 使它与△ABC关于x轴对称:(2)、以点(4,0)为位似中心,在网格中画出ΔABC的位似图形△A2B2C2 , 且△A2B2C2与△ABC的相似比为2:1;(3)、设点P(a,b)为△ABC内一点,则依上述变换后点P在△A2B2C2内的对应点P2的坐标是.17. 如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,过点B作射线BB1∥AC.动点D从点A出发沿射线AC方向以每秒5个单位的速度运动,同时动点E从点C沿射线AC方向以每秒3个单位的速度运动.过点D作DH⊥AB于H,过点E作EF⊥AC交射线BB1于F,G是EF中点,连接DG.设点D运动的时间为t秒.(1)当t为何值时,AD=AB,并求出此时DE的长度;
(2)当△DEG与△ACB相似时,求t的值.
 18. 在矩形 中,已知 ,在边 上取点 ,使 ,连结 ,过点 作 ,与边 或其延长线交于点 .
18. 在矩形 中,已知 ,在边 上取点 ,使 ,连结 ,过点 作 ,与边 或其延长线交于点 .
猜想:如图①,当点 在边 上时,写出线段 与 的大小关系。
探究:如图②,当点 在边 的延长线上时, 与边 交于点 .判断线段 与 的大小关系,并加以证明.
应用:如图②,若 利用探究得到的结论,求线段 的长.