（苏科版）2022-2023学年九年级数学下册6.2 黄金分割同步测试

试卷更新日期：2022-10-25 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 已知点C是线段AB的黄金分割点，且AC＞BC，若AB＝2，则BC的值为（）

A、3 $- \sqrt{5}$ B、1 $+ \sqrt{5}$ C、 $\sqrt{5} -$ 1 D、 $\sqrt{5} -$ 2

查看试题解析
2. 若线段AB=2，点P是线段AB的黄金分割点，且AP $<$ BP，则AP的长为（）

A、 $\sqrt{5} - 1$ B、 $3 - \sqrt{5}$ C、 $\frac{\sqrt{5} - 1}{2}$ D、 $\frac{3 - \sqrt{5}}{2}$

查看试题解析
3. 如图是著名画家达·芬奇的名画《蒙娜丽莎》.画中的脸部被包在矩形ABCD内，点E是AB的黄金分割点，BE＞AE，若AB＝2a，则BE长为（）

A、（ $\sqrt{5}$ +1）a B、（ $\sqrt{5}$ ﹣1）a C、（3﹣ $\sqrt{5}$ ）a D、（ $\sqrt{5}$ ﹣2）a

查看试题解析
4. 已知如图，点C是线段AB的黄金分割点（AC＞BC），则下列结论中正确的是（）

A、AB²=AC²+BC² B、BC²=AC•BA C、AC²=AB•BC D、AC=2BC

查看试题解析
5. 在中华经典美文阅读中，小明同学发现自己的一本书的宽与长之比为黄金比，已知这本书的长为20cm，则它的宽约为（）

A、12.36 cm B、13.6 cm C、32.36 cm D、7.64 cm

查看试题解析
6. 如图，已知△ABC中，AB=3，AC=4，BC=5，作∠ABC的角平分线交AC于D，以D为圆心，DA为半径作圆，与射线交于点E、F．有下列结论：
①△ABC是直角三角形；②⊙D与直线BC相切；③点E是线段BF的黄金分割点；④tan∠CDF=2．
其中正确的结论有（）

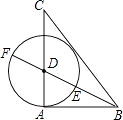A、4个 B、3个 C、2个 D、1个

查看试题解析
7. 有以下命题：
①如果线段d是线段a，b，c的第四比例项，则有 $\frac{a}{b} = \frac{c}{d}$ ；
②如果点C是线段AB的中点，那么AC是AB、BC的比例中项；
③如果点C是线段AB的黄金分割点，且AC＞BC，那么AC是AB与BC的比例中项；
④如果点C是线段AB的黄金分割点，AC＞BC，且AB=2，则AC= $\sqrt{5}$ ﹣1．
其中正确的判断有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 若点C数线段AB的黄金分割点，且AC＞BC，则下列说法正确的有（）
①AB= $\frac{\sqrt{5} + 1}{2}$ AC；②AC=3﹣ $\frac{3 - \sqrt{5}}{2}$ AB；③AB：AC=AC：AB；④AC≈0.618AB．

A、1个 B、2个 C、3个 D、4个

查看试题解析
9. 线段MN长为1cm，点P是MN的黄金分割点，则MP的长是（）

A、 $\frac{\sqrt{5} - 1}{2}$ B、 $\frac{3 - \sqrt{5}}{2}$ C、 $\frac{\sqrt{5} - 1}{2}$ 或 $\frac{3 - \sqrt{5}}{2}$ D、不能确定

查看试题解析
10. 美是一种感觉，当人体下半身长与身高的比值越接近0.618时，越给人一种美感．某女模特身高165cm，下半身长x（cm）与身高l（cm）的比值是0.60．为尽可能达到好的效果，她应穿的高跟鞋的高度大约为（）

A、4cm B、6cm C、8cm D、10cm

查看试题解析

二、填空题（每题3分，共15分）

11. 已知点 $P$ 是线段 $M N$ 的黄金分割点， $M P > N P$ ，且 $MP = (\sqrt{5} - 1) cm$ ，则 $M N$ 等于 $cm$ .

查看试题解析
12. 人体下半身与身高的比例越接近0.618，越给人美感．遗憾的是，即使芭蕾舞演员也达不到如此的完美．某女士身高1.68m，下半身1.02m，她应该选择穿（精确到0.1cm）的高跟鞋看起来更美．

查看试题解析
13. 一个主持人站在舞台的黄金分割点处最自然得体．如果舞台AB长为20米，一个主持人现在站在A处，则它应至少再走米才最理想．（结果精确到0.01米）

查看试题解析
14. 如果点C是线段AB的黄金分割点，AC＞BC，AB=100cm，则BC=cm．

查看试题解析
15. 顶角为36°的等腰三角形称为黄金三角形（即：点D是AC的黄金分割点），如图，在△ABC中，AB=AC=1，∠A=36°，BD是三角形ABC的角平分线，那么AD= ．

查看试题解析

三、解答题（共8题，共55分）

16. 如图，已知等腰△ABC中，顶角∠A=36°，BD为∠ABC的平分线，求证：点D是AC的黄金分割点．

查看试题解析
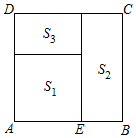
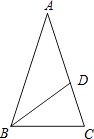17. 如果一个矩形ABCD（AB＜BC）中， $\frac{A B}{B C} = \frac{\sqrt{5} - 1}{2}$ ≈0.618，那么这个矩形称为黄金矩形，黄金矩形给人以美感．在黄金矩形ABCD内作正方形CDEF，得到一个小矩形ABFE（如图），请问矩形ABFE是否是黄金矩形？请说明你的结论的正确性．

查看试题解析
18. 人的肚脐是人的身高的黄金分割点，一般来讲，当肚脐到脚底的长度与身高的比为0.618时，是比较好看的黄金身段．一个身高1.70m的人，他的肚脐到脚底的长度为多少时才是黄金身段（保留两位小数）？

查看试题解析
19. 如图，已知线段AB，P₁是AB的黄金分割点（AP₁＞BP₁），点O是AB的中点，P₂是P₁关于点O的对称点．求证：P₁B是P₂B和P₁P₂的比例中项．

查看试题解析
20.
用纸折出黄金分割点：裁一张正方形的纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落到线段EA上，折出点B的新位置B′，因而EB′＝EB，类似地，在AB上折出点B″使AB″＝AB′，这时B″就是AB的黄金分割点，请你证明这个结论．

查看试题解析
21. 如图，点E是正方形 $A B C D$ 的边 $A B$ 边上的黄金分割点，且 $A E$ ＞ $E B$ ， $S_{1}$ 表示 $A E$ 为边长的正方形面积， $S_{2}$ 表示以 $B C$ 为长， $B E$ 为宽的矩形面积， $S_{3}$ 表示正方形 $A B C D$ 除去 $S_{1}$ 和 $S_{2}$ 剩余的面积，求 $S_{3}$ ： $S_{2}$ 的值．

查看试题解析
22. 如图，在平行四边形ABCD中，E为边AD延长线上的一点，且D为AE的黄金分割点，即 $A D = \frac{\sqrt{5} - 1}{2} A E$ ，BE交DC于点F，已知 $A B = \sqrt{5} + 1$ ，求CF的长 .

查看试题解析
23. 如果一个矩形的宽与长的比是黄金比，那么这个矩形称为黄金矩形．如图，已知四边形ABCD为黄金矩形，以它的宽为边在其内部作正方形AEFD，那么剩下的矩形BCFE也是一个黄金矩形，你能证明这个结论吗？

查看试题解析