（苏科版）2022-2023学年九年级数学下册5.5用二次函数解决问题同步测试

试卷更新日期：2022-10-25 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，抛物线y=ax²+bx+c与x轴交于A，B两点，与y轴交于C点，DE是正三角形ABC的中位线.动点M，N分别从D、E出发，沿着射线DE与射线EB方向移动相同的路程，连结AM，DN交于P点.则下列结论：①ac=-3；②AM=DN；③无论M，N处何位置，∠APN的大小始终不变.其中正确的是（）

A、 $① ②$ B、 $① ③$ C、 $① ② ③$ D、 $② ③$

查看试题解析
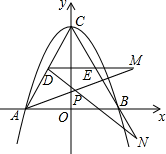2. 若 $\min {a ， b ， c}$ 表示 $a ， b ， c$ 三个数中的最小值，当 $y = \min {x^{2} ， x + 2 ， 8 - x}$ 时 $(x \geq 0)$ ，则 $y$ 的最大值是（）

A、4 B、5 C、6 D、7

查看试题解析
3. 如图，抛物线 $y = \frac{1}{2} x^{2} - 7 x + \frac{45}{2}$ 与x轴交于点A、B，把抛物线在x轴及其下方的部分记作 $C_{1}$ ，将 $C_{1}$ 向左平移得到 $C_{2}$ ， $C_{2}$ 与x轴交于点B、D，若直线 $y = \frac{1}{2} x + m$ 与 $C_{1}$ 、 $C_{2}$ 共有3个不同的交点，则m的取值范围是（）

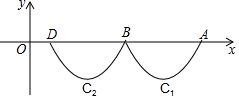A、 $- \frac{45}{8} < m < - \frac{5}{2}$ B、 $- \frac{29}{8} < m < - \frac{1}{2}$ C、 $- \frac{29}{8} < m < - \frac{5}{2}$ D、 $- \frac{45}{8} < m < - \frac{1}{2}$

查看试题解析
4. 图（1）是一个横断面为抛物线形状的拱桥，当水面在l时，拱顶（拱桥洞的最高点）离水面2m，水面宽4m．如图（2）建立平面直角坐标系，则抛物线的关系式是（）

A、y=﹣2x² B、y=2x² C、y=﹣ x² D、y= x²

查看试题解析
5. 某公司的生产利润原来是a元，经过连续两年的增长达到了y万元，如果每年增长的百分数都是x，那么y与x的函数关系是（）

A、y=x²+a B、y=a（x﹣1）² C、y=a（1﹣x）² D、y=a（1+x）²

查看试题解析
6. 如图所示，△DEF中，∠DEF=90°，∠D=30°，DF=16，B是斜边DF上一动点，过B作AB⊥DF于B，交边DE(或边EF)于点A，设BD=x，△ABD的面积为y，则y与x之间的函数图象大致为（）

A、（ B、 C、 D、（

查看试题解析
7. 如图，在矩形纸片ABCD中，AB＝3，BC＝2，沿对角线AC剪开（如图①）；固定△ADC，把△ABC沿AD方向平移（如图②），当两个三角形重叠部分的面积最大时，移动的距离AA′等于（）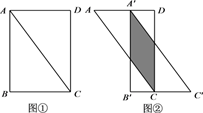

A、1 B、1.5 C、2 D、0.8或1.2

查看试题解析
8. 如图，铅球运动员掷铅球的高度y（m）与水平距离x（m）之间的函数关系式是y=﹣ $\frac{1}{12}$ x²+ $\frac{2}{3}$ x+ $\frac{5}{3}$ ，则该运动员此次掷铅球的成绩是（）

A、6m B、12m C、8m D、10m

查看试题解析
9. 如图，排球运动员站在点O处练习发球，将球从O点正上方2m的A处发出，把球看成点，其运行的高度y（m）与运行的水平距离x（m）满足关系式y=a（x﹣k）²+h．已知球与O点的水平距离为6m时，达到最高2.6m，球网与O点的水平距离为9m．高度为2.43m，球场的边界距O点的水平距离为18m，则下列判断正确的是（）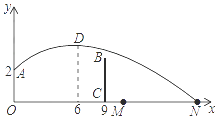

A、球不会过网 B、球会过球网但不会出界 C、球会过球网并会出界 D、无法确定

查看试题解析
10. 足球运动员将足球沿与地面成一定角度的方向踢出，足球飞行的路线是一条抛物线，不考虑空气阻力，足球距离地面的高度h（单位：m）与足球被踢出后经过的时间t（单位：s）之间的关系如下表：
t
0
1
2
3
4
5
6
7
…
h
0
8
14
18
20
20
18
14
…
下列结论：①足球距离地面的最大高度为20m；②足球飞行路线的对称轴是直线t= $\frac{9}{2}$ ；③足球被踢出9s时落地；④足球被踢出1.5s时，距离地面的高度是11m．其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题（每题3分，共15分）

11. 将抛物线y＝﹣x²﹣4x（﹣4≤x≤0）沿y轴折叠后得另一条抛物线，若直线y＝x+b与这两条抛物线共有3个公共点，则b的取值范围为.

查看试题解析
12. 如图，已知二次函数 $y_{1} = \frac{2}{3} x^{2} - \frac{4}{3} x$ 的图象与正比例函数 $y_{2} = \frac{2}{3} x$ 的图象交于点 $A (3 ， 2)$ ，与 $x$ 轴交于点 $B (2 ， 0)$ ，若 $0 < y_{1} < y_{2}$ ，则 $x$ 的取值范围是．

查看试题解析
13. 如图，抛物线 $y = \frac{1}{2} x^{2} - x - \frac{3}{2}$ 的图象与坐标轴交于点A ， B ， D ，顶点为E ，以AB为直径画半圆交y正半轴交于点C ，圆心为M ， P是半圆上的一动点，连接EP ． ①点E在⊙M的内部；②CD的长为 $\frac{3}{2} + \sqrt{3}$ ；③若P与C重合，则∠DPE＝15°；④在P的运动过程中，若AP＝ $\sqrt{6}$ ，则PE＝ $\sqrt{5} + \sqrt{3}$ ⑤N是PE的中点，当P沿半圆从点A运动至点B时，点N运动的路径长是2π．其中结论正确的是

查看试题解析
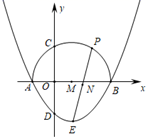14. 二次函数 $y = - x^{2} - 2 x$ 图象 $x$ 轴上方的部分沿 $x$ 轴翻折到 $x$ 轴下方，图象的其余部分保持不变，翻折后的图象与原图象 $x$ 轴下方的部分组成一个“ $M$ ”形状的新图象，若直线 $y = \frac{1}{2} x + b$ 与该新图象有两个公共点，则 $b$ 的取值范围为.

查看试题解析
15. 如果直线y=kx+b与抛物线y= $\frac{1}{4}$ x²交于A（x₁ ， y₁），B（x₂ ， y₂）两点，当OA⊥OB时，直线AB恒过一个定点，该定点坐标为． [提示：直线l₁：y=k₁x+b₁与直线l₂：y=k₂x+b₂互相垂直，则k₁•k₂=-1]

查看试题解析

三、解答题（共8题，共55分）

16. 如图，用50m长的护栏全部用于建造一块靠墙的长方形花园，写出长方形花园的面积y（m²）与它与墙平行的边的长x（m）之间的函数．

查看试题解析
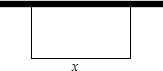17. 如图所示，在矩形ABCD中，AB=6厘米，BC=12厘米，点P在线段AB上，P从点A开始沿AB边以1厘米/秒的速度向点B移动．点E为线段BC的中点，点Q从E点开始，沿EC以1厘米/秒的速度向点C移动．如果P、Q同时分别从A、E出发，写出出发时间t与△BPQ的面积S的函数关系式，求出t的取值范围．

查看试题解析
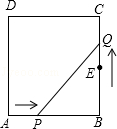18. 已知某商场一月份的利润是100万元，三月份的利润达到y万元，这两个月的利润月平均增长率为x，求y与x的函数关系式．

查看试题解析
19. 用总长为L米的篱笆围成长方形场地，已知长方形的面积为60m² ，一边长度x米，求L与x之间的关系式，并写出自变量x的取值范围．

查看试题解析
20.
如图1，已知二次函数y=x²+bx+c的图象与x轴交于A(-1，0)、B(3，0)两点，与y轴交于点C，顶点为D，对称轴为直线l ，

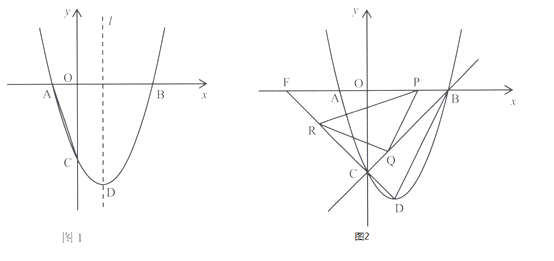(1)、求该二次函数的表达式；

(2)、若点E是对称轴l右侧抛物线上一点，且S_△ADE=2S_△AOC ，求点E的坐标；

(3)、如图2，连接DC并延长交x轴于点F，设P为线段BF上一动点(不与B、F重合)，过点P作PQ $∥$ BD交直线BC于点Q，将直线PQ绕点P沿顺时针方向旋转45 $°$ 后，所得的直线交DF于点R，连接OR．请直接写出当△PQR与△PFR相似时点P的坐标．

查看试题解析
21.
音乐喷泉（图1）可以使喷水造型随音乐的节奏起伏变化而变化．某种音乐喷泉形状如抛物线，设其出水口为原点，出水口离岸边18m，音乐变化时，抛物线的顶点在直线y=kx上变动，从而产生一组不同的抛物线（图2），这组抛物线的统一形式为y=ax²+bx．
（1）若已知k=1，且喷出的抛物线水线最大高度达3m，求此时a、b的值；
（2）若k=1，喷出的水恰好达到岸边，则此时喷出的抛物线水线最大高度是多少米？
（3）若k=3，a=﹣ $\frac{2}{7}$ ，则喷出的抛物线水线能否达到岸边？

查看试题解析
22. 某商场销售一种成本为每件20元的商品，销售过程中发现，每月销售量y（件）与销售单价x（元）之间的关系可近似的看作一次函数：y=﹣10x+500．
（1）设商场销售该种商品每月获得利润为w（元），写出w与x之间的函数关系式；
（2）如果商场想要销售该种商品每月获得2000元的利润，那么每月成本至少多少元？
（3）为了保护环境，政府部门要求用更加环保的新产品替代该种商品，商场若销售新产品，每月销售量与销售价格之间的关系与原产品的销售情况相同，新产品为每件22元，同时对商场的销售量每月不小于150件的商场，政府部门给予每件3元的补贴，试求定价多少时，新产品每月可获得销售利润最大？并求最大利润．

查看试题解析
23.
如图，抛物线y=﹣x²+bx+c交x轴负半轴于点A，交X轴正半轴于点B，交y轴正半轴于点C，直线BC的解析式为y=kx+3（k≠0 ），∠ABC=45°
（1）求b、c的值；
（2）点P在第一象限的抛物线上，过点P分别作x轴、y轴的平行线，交直线BC于点M、N，设点P的横坐标为t，线段MN的长为d，求d与t之间的函数关系式（不要求写出自变量t的取值范围）；
（3）在（2）的条件下，点E为抛物线的顶点，连接EC、EP、AP，AP交y轴于点D，连接DM，若∠DMB=90°，求四边形CMPE的面积．

查看试题解析

t	0	1	2	3	4	5	6	7	…
h	0	8	14	18	20	20	18	14	…

（苏科版）2022-2023学年九年级数学下册5.5用二次函数解决问题 同步测试

一、单选题（每题3分，共30分）

二、填空题（每题3分，共15分）

三、解答题（共8题，共55分）

（苏科版）2022-2023学年九年级数学下册5.5用二次函数解决问题同步测试