2022年秋季浙教版数学九年级上学期期中复习检测A
试卷更新日期:2022-10-25 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 下列事件为确定事件的有( )
(1)打开电视正在播动画片(2)长、宽为 , 的矩形面积是(3)掷一枚质地均匀的硬币,正面朝上(4)是无理数A、1个 B、2个 C、3个 D、4个2. 已知二次函数 ,当函数值y随x值的增大而增大时,x的取值范围是( )A、 B、 C、 D、3. 如图, 内接于 ,CD是 的直径, ,则 ( )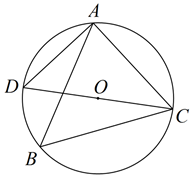 A、70° B、60° C、50° D、40°4. 在某市组织的物理实验操作考试中,考试所用实验室共有24个测试位,分成6组,同组4个测试位各有一道相同试题,各组的试题不同,分别标记为A,B,C,D,E,F,考生从中随机抽取一道试题,则某个考生抽到试题A的概率为( )A、 B、 C、 D、5. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( )
A、70° B、60° C、50° D、40°4. 在某市组织的物理实验操作考试中,考试所用实验室共有24个测试位,分成6组,同组4个测试位各有一道相同试题,各组的试题不同,分别标记为A,B,C,D,E,F,考生从中随机抽取一道试题,则某个考生抽到试题A的概率为( )A、 B、 C、 D、5. 二次函数y=ax2+bx+c的图象如图所示,则一次函数y=bx+c和反比例函数y=在同一平面直角坐标系中的图象可能是( ) A、
A、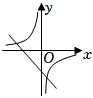 B、
B、 C、
C、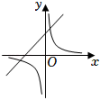 D、
D、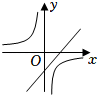 6. 如图,在Rt△ABC中, , , , 将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为( )
6. 如图,在Rt△ABC中, , , , 将绕点B顺时针旋转90°得到.在此旋转过程中所扫过的面积为( ) A、25π+24 B、5π+24 C、25π D、5π7. 函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )
A、25π+24 B、5π+24 C、25π D、5π7. 函数的图象是由函数的图象轴上方部分不变,下方部分沿轴向上翻折而成,如图所示,则下列结论正确的是( )① ;②;③;④将图象向上平移1个单位后与直线有3个交点.
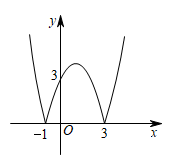 A、①② B、①③ C、②③④ D、①③④8. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .
A、①② B、①③ C、②③④ D、①③④8. 如图,二次函数的图象关于直线对称,与x轴交于 , 两点,若 , 则下列四个结论:① , ② , ③ , ④ .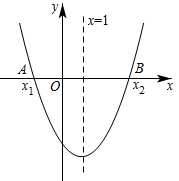
正确结论的个数为( )
A、1个 B、2个 C、3个 D、4个9. 如图,AB是⊙O的直径,PA与⊙O相切于点A,∠ABC=25°,OC的延长线交PA于点P,则∠P的度数是( )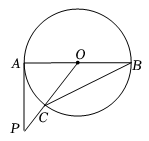 A、25° B、35° C、40° D、50°10. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为 , 且经过点(-1,0).下列结论:①3a+b=0;②若点 , (3,y2)是抛物线上的两点,则y1<y2;③10b-3c=0;④若y≤c,则0≤x≤3.其中正确的有( )
A、25° B、35° C、40° D、50°10. 已知二次函数y=ax2+bx+c(a≠0)的部分图象如图所示,对称轴为 , 且经过点(-1,0).下列结论:①3a+b=0;②若点 , (3,y2)是抛物线上的两点,则y1<y2;③10b-3c=0;④若y≤c,则0≤x≤3.其中正确的有( )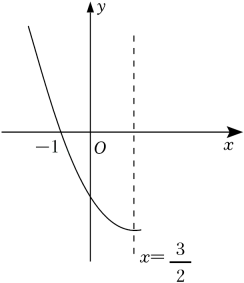 A、1个 B、2个 C、3个 D、4个
A、1个 B、2个 C、3个 D、4个二、填空题(每题3分,共18分)
-
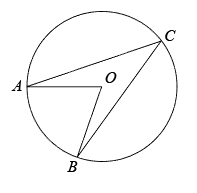
11. 已知二次函数 , 当时,函数值y的最小值为1,则a的值为 .12. 如图,A、B、C点在圆O上, 若∠ACB=36°, 则∠AOB= .
 13. 在北京冬奥会自由式滑雪大跳台比赛中,我国选手谷爱凌的精彩表现让人叹为观止,已知谷爱凌从2m高的跳台滑出后的运动路线是一条抛物线,设她与跳台边缘的水平距离为xm,与跳台底部所在水平面的竖直高度为ym,y与x的函数关系式为y=x2+x+2(0≤x≤20.5),当她与跳台边缘的水平距离为m时,竖直高度达到最大值.
13. 在北京冬奥会自由式滑雪大跳台比赛中,我国选手谷爱凌的精彩表现让人叹为观止,已知谷爱凌从2m高的跳台滑出后的运动路线是一条抛物线,设她与跳台边缘的水平距离为xm,与跳台底部所在水平面的竖直高度为ym,y与x的函数关系式为y=x2+x+2(0≤x≤20.5),当她与跳台边缘的水平距离为m时,竖直高度达到最大值.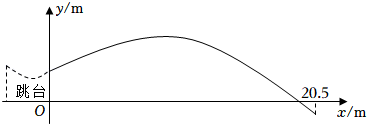 14. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).
14. 某食品零售店新上架一款冷饮产品,每个成本为8元,在销售过程中,每天的销售量y(个)与销售价格x(元/个)的关系如图所示,当时,其图象是线段AB,则该食品零售店每天销售这款冷饮产品的最大利润为元(利润=总销售额-总成本).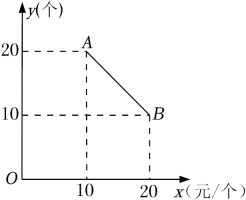 15. 如图,边长为4的正方形ABCD内接于 , 则的长是(结果保留)
15. 如图,边长为4的正方形ABCD内接于 , 则的长是(结果保留) 16. 小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 . (填序号,多选、少选、错选都不得分)
16. 小明在学习“二次函数”内容后,进行了反思总结.如图,二次函数y=ax2+bx+c(a≠0)图像的一部分与x轴的一个交点坐标为(1,0),对称轴为直线x=﹣1,结合图像他得出下列结论:①ab>0且c>0;②a+b+c=0;③关于x的一元二次方程ax2+bx+c=0(a≠0)的两根分别为﹣3和1;④若点(﹣4,y1),(﹣2,y2),(3,y3)均在二次函数图象上,则y1<y2<y3;⑤3a+c<0,其中正确的结论有 . (填序号,多选、少选、错选都不得分)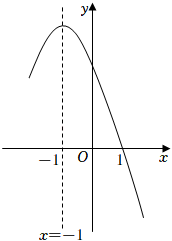
三、解答题(共8题,共72分)
-
17. 教育部在《大中小学劳动教育指导纲要(试行)》中明确要求:初中生每周课外生活和家庭生活中,劳动时间不少于3小时.某走读制初级中学为了解学生劳动时间的情况,对学生进行了随机抽样调查,并将调查结果制成不完整的统计图表,如图:
平均每周劳动时间的频数统计表
劳动时间小时
频数
t<3
9
3≤t<4
a
4≤t<5
66
t≥5
15

请根据图表信息,回答下列问题.
(1)、参加此次调查的总人数是人,频数统计表中a=;(2)、在扇形统计图中,D组所在扇形的圆心角度数是°;(3)、该校准备开展以“劳动美”为主题的教育活动,要从报名的2男2女中随机挑选2人在活动中分享劳动心得,请用树状图或列表法求恰好抽到一名男生和一名女生的概率.18. 石拱桥是我国古代人民勤劳和智慧的结晶(如图1),隋代建造的赵州桥距今约有1400年历史,是我国古代石拱桥的代表.如图2是根据某石拱桥的实物图画出的几何图形,桥的主桥拱是圆弧形,表示为 .桥的跨度(弧所对的弦长) ,设 所在圆的圆心为 ,半径 ,垂足为 .拱高(弧的中点到弦的距离) .连接 .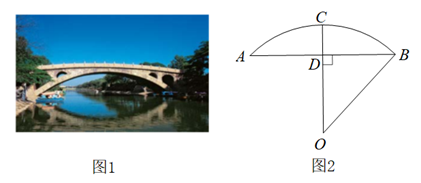 (1)、直接判断 与 的数量关系;(2)、求这座石拱桥主桥拱的半径(精确到 ).19. 端午节吃粽子是中华民族的传统习俗,市场上猪肉粽进价比豆沙粽进价每盒贵10元,一盒猪肉粽加两盒豆沙粽进价为100元.(1)、求每盒猪肉粽和豆沙粽的进价;(2)、在销售中,某商家发现当每盒猪肉粽售价为50元时,每天可售出100盒,若每盒售价提高1元,则每天少售出2盒.设每盒猪肉粽售价为元,销售猪肉粽的利润为元,求该商家每天销售猪肉粽获得的最大利润.20. 如图,△ABC内接于⊙O,交⊙O于点D,交BC于点E,交⊙O于点F,连接AF,CF.
(1)、直接判断 与 的数量关系;(2)、求这座石拱桥主桥拱的半径(精确到 ).19. 端午节吃粽子是中华民族的传统习俗,市场上猪肉粽进价比豆沙粽进价每盒贵10元,一盒猪肉粽加两盒豆沙粽进价为100元.(1)、求每盒猪肉粽和豆沙粽的进价;(2)、在销售中,某商家发现当每盒猪肉粽售价为50元时,每天可售出100盒,若每盒售价提高1元,则每天少售出2盒.设每盒猪肉粽售价为元,销售猪肉粽的利润为元,求该商家每天销售猪肉粽获得的最大利润.20. 如图,△ABC内接于⊙O,交⊙O于点D,交BC于点E,交⊙O于点F,连接AF,CF.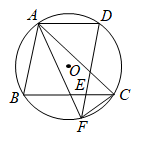 (1)、求证:AC=AF;(2)、若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).21. 在平面直角坐标系xOy中,已知抛物线y=-x2+bx+c经过点A(-1,0)和点B(0,3),顶点为C,点D在其对称轴上,且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.
(1)、求证:AC=AF;(2)、若⊙O的半径为3,∠CAF=30°,求的长(结果保留π).21. 在平面直角坐标系xOy中,已知抛物线y=-x2+bx+c经过点A(-1,0)和点B(0,3),顶点为C,点D在其对称轴上,且位于点C下方,将线段DC绕点D按顺时针方向旋转90°,点C落在抛物线上的点P处.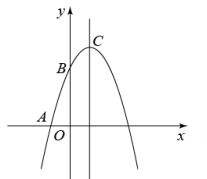 (1)、求抛物线的解析式;(2)、求点P的坐标;(3)、将抛物线平移,使其顶点落在原点O,这时点P落在点E的位置,在y轴上是否存在点M,使得MP+ME的值最小,若存在,求出点M的坐标;若不存在,请说明理由.22. 如图,点A、B、C在圆O上,∠ABC=60°,直线AD∥BC,AB=AD,点O在BD上.
(1)、求抛物线的解析式;(2)、求点P的坐标;(3)、将抛物线平移,使其顶点落在原点O,这时点P落在点E的位置,在y轴上是否存在点M,使得MP+ME的值最小,若存在,求出点M的坐标;若不存在,请说明理由.22. 如图,点A、B、C在圆O上,∠ABC=60°,直线AD∥BC,AB=AD,点O在BD上.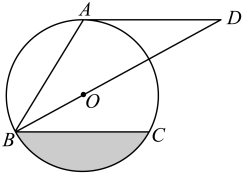 (1)、判断直线AD与圆O的位置关系,并说明理由;(2)、若圆的半径为6,求图中阴影部分的面积.23. 定义:函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“n阶方点”.例如,点是函数图像的“阶方点”;点是函数图像的“2阶方点”.(1)、在①;②;③三点中,是反比例函数图像的“1阶方点”的有(填序号);(2)、若y关于x的一次函数图像的“2阶方点”有且只有一个,求a的值;(3)、若y关于x的二次函数图像的“n阶方点”一定存在,请直接写出n的取值范围.24. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.
(1)、判断直线AD与圆O的位置关系,并说明理由;(2)、若圆的半径为6,求图中阴影部分的面积.23. 定义:函数图象上到两坐标轴的距离都不大于的点叫做这个函数图象的“n阶方点”.例如,点是函数图像的“阶方点”;点是函数图像的“2阶方点”.(1)、在①;②;③三点中,是反比例函数图像的“1阶方点”的有(填序号);(2)、若y关于x的一次函数图像的“2阶方点”有且只有一个,求a的值;(3)、若y关于x的二次函数图像的“n阶方点”一定存在,请直接写出n的取值范围.24. 如图,在平面直角坐标系中,经过点的直线AB与y轴交于点 . 经过原点O的抛物线交直线AB于点A,C,抛物线的顶点为D.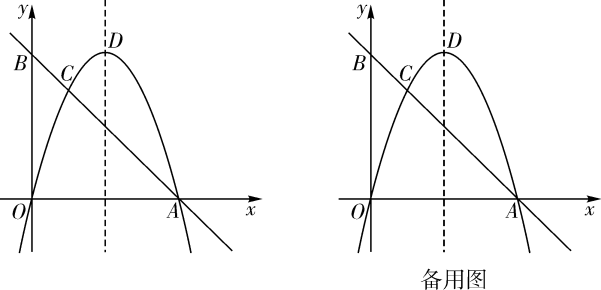 (1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.
(1)、求抛物线的表达式;(2)、M是线段AB上一点,N是抛物线上一点,当轴且时,求点M的坐标;(3)、P是抛物线上一动点,Q是平面直角坐标系内一点.是否存在以点A,C,P,Q为顶点的四边形是矩形?若存在,直接写出点Q的坐标;若不存在,请说明理由.