（苏科版）2022-2023学年九年级数学下册5.1二次函数 同步测试
试卷更新日期：2022-10-25 类型：同步测试
一、单选题
-
1. 下列函数中，属于二次函数的是（ ）A、y=2x﹣3 B、y=（x+1）2﹣x2 C、y=2x2﹣7x D、y=﹣2. 已知函数①y=5x﹣4，②t= x2﹣6x，③y=2x3﹣8x2+3，④y= x2﹣1，⑤y= +2，其中二次函数的个数为（ ）A、1 B、2 C、3 D、43. 若y=ax2﹣x+2是y关于x的二次函数，则a的取值范围是（ ）A、a＞0 B、a＜0 C、a≠0 D、a≠24. 如图，铅球的出手点C距地面1米，出手后的运动路线是抛物线，出手后4秒钟达到最大高度3米，则铅球运行路线的解析式为（ ）
A、h=﹣ t2 B、y=﹣ t2+t C、h=﹣ t2+t+1 D、h=﹣ t2+2t+15. 在半径为4的圆中，挖去一个边长为xcm的正方形，剩下部分面积为ycm2 ， 则关于y与x之间函数关系式为（ ）A、y=πx2﹣4y B、y=16π﹣x2 C、y=16﹣x2 D、y=x2﹣4y6. 某乡镇企业现在年产值是15万元，如果每增加100元投资，一年增加250元产值，那么总产值y（万元）与新增加的投资额x（万元）之间函数关系为（ ）A、y=25x+15 B、y=2.5x+1.5 C、y=2.5x+15 D、y=25x+1.57. 把一根长为50cm的铁丝弯成一个长方形，设这个长方形的一边长为x（cm），它的面积为y（cm2），则y与x之间的函数关系式为（ ）A、y=﹣x2+50x B、y=x2﹣50x C、y=﹣x2+25x D、y=﹣2x2+258. 三角形的一边长与这边上的高都为xcm，其面积是ycm2 ， 则y与x的函数关系为（ ）A、y=x2 B、y=2x2 C、y= x2 D、y= x29. 是二次函数，则m的值为（ ）
A、0，﹣2 B、0，2 C、0 D、-210. 若函数y=a是二次函数且图象开口向上，则a=（ ）
A、-2 B、4 C、4或﹣2 D、4或3二、填空题
-
11. 二次函数y=x2+4x﹣3中，当x=﹣1时，y的值是 ．12. 若y=（3﹣m） 是二次函数，则m= ．13. 若y=xm﹣1+2x是二次函数，则m= ．14. 如图，在直角梯形ABCD中，BF=AE=DG=x，AB=6，CD=3，AD=4，则四边形CGEF的面积y与x之间的函数关系式为 ， 自变量x的取值范围是 ．
15. 人民币一年定期的年利率为x，一年到期后，银行将本金和利息自动按一年定期储蓄转存．如果存款额是a元，则两年后的本息和y（元）的表达式为（不考虑利息税）．三、解答题
-
16. 当k为何值时，函数y=（k﹣1） +1为二次函数？17. 若函数y=（m+1）x 是二次函数，求m的值．18. 如图，等腰梯形的周长为60，底角为30°，腰长为x，面积为y，试写出y与x的函数表达式．
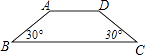19. 如图，在△ABC中，∠B=90°，AB=12，BC=24，动点P从点A开始沿边AB向终点B以每秒2个单位长度的速度移动，动点Q从点B开始沿边BC以每秒4个单位长度的速度向终点C移动，如果点P、Q分别从点A、B同时出发，那么△PBQ的面积S随出发时间t（s）如何变化？写出函数关系式及t的取值范围．
20. 如图，用50m长的护栏全部用于建造一块靠墙的长方形花园，写出长方形花园的面积y（m2）与它与墙平行的边的长x（m）之间的函数．
21. 已知函数y=（m+2）+1是关于x的二次函数．（1）满足条件的m的值；
（2）m为何值时，抛物线有最低点？求出这个最低点，这时当x为何值时，y随x的增大而增大？
（3）m为何值时，函数有最大值？最大值是多少？这时当x为何值时，y随x的增大而减小？