(华师大版)2022-2023学年九年级数学下册27.4 正多边形和圆 同步测试
试卷更新日期:2022-10-24 类型:同步测试
一、单选题
-
1. 如图,正方形ABCD内接于⊙O,点P在正上,则∠P的度数为( )
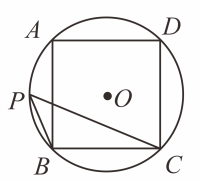 A、30° B、45° C、60° D、90°2. 如图,正六边形ABCDEF内接于于⊙O,连接BD,则∠CBD的度数是( )
A、30° B、45° C、60° D、90°2. 如图,正六边形ABCDEF内接于于⊙O,连接BD,则∠CBD的度数是( )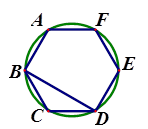 A、30° B、45° C、60° D、90°3. 一个圆的内接正六边形的边长为 2,则该圆的内接正方形的边长为( )A、 B、2 C、2 D、44. 正六边形内切圆面积与外接圆面积之比为( )A、 B、
A、30° B、45° C、60° D、90°3. 一个圆的内接正六边形的边长为 2,则该圆的内接正方形的边长为( )A、 B、2 C、2 D、44. 正六边形内切圆面积与外接圆面积之比为( )A、 B、 C、
D、
5. 半径为8cm的圆的内接正三角形的边长为( )A、8 cm B、4 cm C、8cm D、4cm6. 如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )
C、
D、
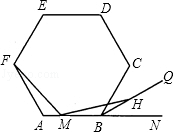
5. 半径为8cm的圆的内接正三角形的边长为( )A、8 cm B、4 cm C、8cm D、4cm6. 如图,由7个形状,大小完全相同的正六边形组成的网格,正六边形的顶点称为格点,已知每个正六边形的边长为1,△ABC的顶点都在格点上,则△ABC的面积是( )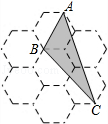 A、 B、2 C、 D、37. 如图,⊙O是正五边形ABCDE的外接圆,点P是 的一点,则∠CPD的度数是( )
A、 B、2 C、 D、37. 如图,⊙O是正五边形ABCDE的外接圆,点P是 的一点,则∠CPD的度数是( ) A、30° B、36° C、45° D、72°8. 以下说法正确的是( )A、每个内角都是120°的六边形一定是正六边形 B、正n边形的对称轴不一定有n条. C、正n边形的每一个外角度数等于它的中心角度数. D、正多边形一定既是轴对称图形,又是中心对称图形.9. 如图,若正方形A 1B1C1D1内接于正方形ABCD的内接圆,则 的值为( )
A、30° B、36° C、45° D、72°8. 以下说法正确的是( )A、每个内角都是120°的六边形一定是正六边形 B、正n边形的对称轴不一定有n条. C、正n边形的每一个外角度数等于它的中心角度数. D、正多边形一定既是轴对称图形,又是中心对称图形.9. 如图,若正方形A 1B1C1D1内接于正方形ABCD的内接圆,则 的值为( )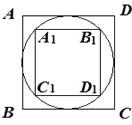 A、 B、 C、 D、10. 若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3 , r4 , r6 , 则r3:r4:r6等于( )
A、 B、 C、 D、10. 若同一个圆的内角正三角形、正方形、正六边形的边心距分别为r3 , r4 , r6 , 则r3:r4:r6等于( )
A、 B、 C、 D、二、填空题
-
11. 如图所示,正六边形ABCDEF内接于圆O,则∠ADB的度数为 .
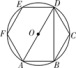 12. 半径为4的圆的内接正三角形的边长为 .13. 如图,正五边形 内接于 ,点 在弧 上,则 的度数为
12. 半径为4的圆的内接正三角形的边长为 .13. 如图,正五边形 内接于 ,点 在弧 上,则 的度数为 14. 如图,已知正六边形ABCDEF的外接圆半径为2cm,则正六边形的边心距是cm.
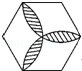
14. 如图,已知正六边形ABCDEF的外接圆半径为2cm,则正六边形的边心距是cm. 15. 半径为2的圆被四等分切割成四条相等的弧,将四个弧首尾顺次相连拼成如图所示的恒星图型,那么这个恒星的面积等于.
15. 半径为2的圆被四等分切割成四条相等的弧,将四个弧首尾顺次相连拼成如图所示的恒星图型,那么这个恒星的面积等于.
三、解答题
-
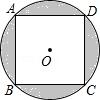
16. 正六边形的边长为8,则阴影部分的面积是多少?
 17. 如图,某圆形场地内有一个内接于⊙O的正方形中心场地,若⊙O的半径为10米,求图中所画的一块草地的面积.(计算结果保留π)
17. 如图,某圆形场地内有一个内接于⊙O的正方形中心场地,若⊙O的半径为10米,求图中所画的一块草地的面积.(计算结果保留π)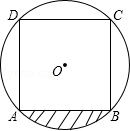 18. 如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.
18. 如图,分别求出半径为R的圆内接正三角形圆内接正方形的周长和面积.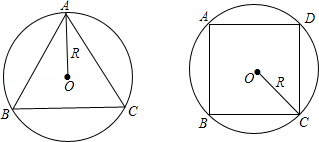 19. 如图五边形ABCDE内接于⊙O,∠A =∠B=∠C=∠D=∠E.
19. 如图五边形ABCDE内接于⊙O,∠A =∠B=∠C=∠D=∠E.求证:五边形ABCDE是正五边形
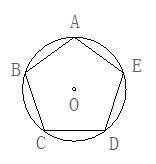 20. 如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.
20. 如图,已知正n边形边长为a,边心距为r,求正n边形的半径R、周长P和面积S.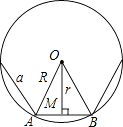
四、综合题
-
21. 如图,正五边形ABCD中,点F、G分别是BC、CD的中点,AF与BG相交于H.
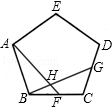 (1)、求证:△ABF≌△BCG;(2)、求∠AHG的度数.
(1)、求证:△ABF≌△BCG;(2)、求∠AHG的度数.