(华师大版)2022-2023学年九年级数学下册27.3圆中的计算问题线 同步测试
试卷更新日期:2022-10-24 类型:同步测试
一、单选题
-
1. 如图所示是某几何体的三视图,根据图中数据计算,这个几何体的侧面积为( ).
 A、 B、12π C、 D、24π2. 如图,一个圆锥形漏斗的底面半径OA=5cm,高OC=12cm.则它的侧面积是( )
A、 B、12π C、 D、24π2. 如图,一个圆锥形漏斗的底面半径OA=5cm,高OC=12cm.则它的侧面积是( ) A、130cm2 B、65πcm2 C、60πcm2 D、30cm23. 底面半径为3,高为4的圆锥侧面积为( )A、15π B、20π C、25π D、30π4. 扇形的半径为 , 扇形的面积 , 则该扇形的圆心角为( )A、 B、 C、 D、5. 如图,在Rt△ABC中,∠A= 90° ,AB=AC=4.分别以点B,C为圆心,线段BC长的一半为半径作圆弧,交AB,BC,AC于点D,E,F,则图中阴影部分的面积是( )
A、130cm2 B、65πcm2 C、60πcm2 D、30cm23. 底面半径为3,高为4的圆锥侧面积为( )A、15π B、20π C、25π D、30π4. 扇形的半径为 , 扇形的面积 , 则该扇形的圆心角为( )A、 B、 C、 D、5. 如图,在Rt△ABC中,∠A= 90° ,AB=AC=4.分别以点B,C为圆心,线段BC长的一半为半径作圆弧,交AB,BC,AC于点D,E,F,则图中阴影部分的面积是( ) A、16-2π B、8-4π C、8-2π D、4-π6. 如图,在30°直角三角板ABC中,点M是斜边AB边上的中点,将三角板绕直角顶点C按顺时针方向旋转90°后得到△A′B′C,若AC=6,则点M经过的的路径长为( )
A、16-2π B、8-4π C、8-2π D、4-π6. 如图,在30°直角三角板ABC中,点M是斜边AB边上的中点,将三角板绕直角顶点C按顺时针方向旋转90°后得到△A′B′C,若AC=6,则点M经过的的路径长为( )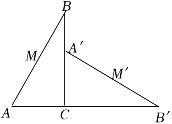 A、6 B、2π C、3π D、4π7. 如图,AB是⊙O的直径,且AB=4,C是⊙O上一点,将 沿直线AC翻折,若翻折后的圆弧恰好经过点O,则图中阴影部分的面积为( )
A、6 B、2π C、3π D、4π7. 如图,AB是⊙O的直径,且AB=4,C是⊙O上一点,将 沿直线AC翻折,若翻折后的圆弧恰好经过点O,则图中阴影部分的面积为( ) A、 B、 C、 D、8. 已知圆锥的底面半径为3cm,高为4cm,则这个圆锥的侧面积为( )A、30π B、24π C、15π D、12π9. 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径 ,扇形圆心解 ,则该圆锥母线长为( )
A、 B、 C、 D、8. 已知圆锥的底面半径为3cm,高为4cm,则这个圆锥的侧面积为( )A、30π B、24π C、15π D、12π9. 如图,沿一条母线将圆锥侧面剪开并展开,得到一个扇形,若圆锥底面半径 ,扇形圆心解 ,则该圆锥母线长为( )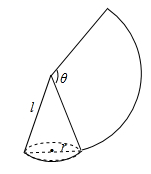 A、10 B、 C、6 D、810. 如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长均为1cm,则这个圆锥的底面半径为( )cm
A、10 B、 C、6 D、810. 如图,扇形OAB是圆锥的侧面展开图,若小正方形方格的边长均为1cm,则这个圆锥的底面半径为( )cm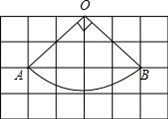 A、 B、 C、 D、2
A、 B、 C、 D、2二、填空题
-
11. 如图,从一块直径是的圆形铁皮上剪出一个圆心角为90°的扇形,如果将剪下来的扇形围成一个圆锥,圆锥的底面圆的半径为m.
 12. 半径为10cm,母线长为15cm的圆锥的侧面积为.13. 如图,已知的对角线 , 将绕其对称中心旋转 , 则点所转过的路径长为.
12. 半径为10cm,母线长为15cm的圆锥的侧面积为.13. 如图,已知的对角线 , 将绕其对称中心旋转 , 则点所转过的路径长为. 14. 已知圆锥的底面圆直径是2,母线是3,则圆锥的侧面积是.15. 已知圆锥的侧面积为 ,底面半径为4,则该圆锥的母线等于.
14. 已知圆锥的底面圆直径是2,母线是3,则圆锥的侧面积是.15. 已知圆锥的侧面积为 ,底面半径为4,则该圆锥的母线等于.三、解答题
-
16. 在 中, 为直径, 为 上一点.
(Ⅰ)如图①,过点 作 的切线,与 的延长线相交于点 ,若 ,求 的大小;
(Ⅱ)如图②, 为优弧 上一点,且 的延长线经过 的中点 ,连接 与 相交于点 ,若 ,求 的大小.
 17. 如图扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,求贴纸部分的面积.
17. 如图扇形纸扇完全打开后,外侧两竹条AB、AC的夹角为120°,AB长为30cm,贴纸部分BD长为20cm,求贴纸部分的面积.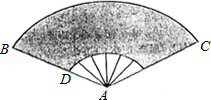 18. 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,OC=2,求阴影部分图形的面积(结果保留π).
18. 如图,AB是⊙O的直径,弦CD⊥AB于点E,∠CDB=30°,OC=2,求阴影部分图形的面积(结果保留π). 19. 如图①是某校存放学生自行车的车棚的示意图(尺寸如图所示,单位:m),车棚顶部是圆柱侧面的一部分,其展开图是矩形;如图②是车棚顶部截面的示意图, 所在圆的圆心为点O,车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积.(不考虑接缝等因素,计算结果保留π)
19. 如图①是某校存放学生自行车的车棚的示意图(尺寸如图所示,单位:m),车棚顶部是圆柱侧面的一部分,其展开图是矩形;如图②是车棚顶部截面的示意图, 所在圆的圆心为点O,车棚顶部是用一种帆布覆盖的,求覆盖棚顶的帆布的面积.(不考虑接缝等因素,计算结果保留π) 20. 将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4cm、宽为3cm的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?(结果保留π)
20. 将一个长方形绕它的一边所在的直线旋转一周,得到的几何体是圆柱,现在有一个长为4cm、宽为3cm的长方形,分别绕它的长、宽所在的直线旋转一周,得到不同的圆柱体,它们的体积分别是多大?(结果保留π)


