（华师大版）2022-2023学年九年级数学下册27.2.3切线 同步测试
试卷更新日期：2022-10-24 类型：同步测试
一、单选题
-
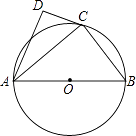
1. 如图，AC是⊙O的切线，切点为C，BC是⊙O的直径，AB交⊙O于点D，连接OD，若∠BAC＝55°，则∠COD的大小为（ ）
A、70° B、60° C、55° D、35°2. 已知：如图，⊙O是△ABC的外接圆，⊙O的直径为10，过点C作⊙O的切线交AB延长线于点P.BC＝6，则B到CP的距离为（ ）
A、 B、3 C、 D、3. 矩形ABCD中，AB＝12，BC＝8，将矩形沿MN折叠，使点C恰好落在AD边的中点F处，以矩形对称中心O点为圆心的圆与FN相切于点G，则⊙O的半径为（ ）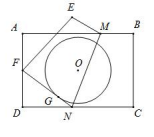
A、3.6 B、 C、3.5 D、4. 如图，△ABC是⊙O的内接三角形，∠C＝70°，过点A的圆的切线交射线BO于点P，则∠P的度数是（ ）
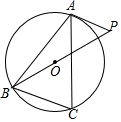A、60° B、50° C、45° D、40°5. 若⊙O半径是2，点A在直线l上，且OA=2，则直线l与⊙O的位置关系是（ ）A、相切 B、相交 C、相离 D、相切或相交6. 如图，在 中，AB是直径，AC是弦，过点C的切线与AB的延长线交于点D，若 ，则 的大小为
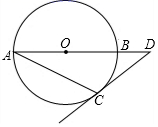A、 B、 C、 D、7. 如图，已知 的直径 与弦 的夹角为 ，过 点的切线 与 的延长线交于点 ，则 等于（ ）
A、 B、 C、 D、8. 如图，AB为⊙O的直径，C为⊙O外一点，过点C作的⊙O切线，切点为B，连接AC交⊙O于D，∠C=38°.点E在AB右侧的半圆上运动（不与A，B重合），则∠AED的大小是（ ）
A、19° B、32° C、38° D、76°9. 如图，在△ABC中，AB＝AC，∠B＝30°，以点A为圆心，以3cm为半径作⊙A.若BC与⊙A相切，则AB的长为（ ）cm.
A、3 B、3 C、6 D、210. 如图，AB是⊙O的弦，AC是⊙O的切线，A为切点，BC经过圆心O.若∠B=20°，则∠C的大小等于（ ）
A、20° B、25° C、40° D、50°二、填空题
-
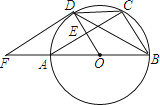
11. 如图，已知PA、PB是⊙O的两条切线，A、B为切点．AC是⊙O 的直径，若∠P=80°，则∠BAC的度数为 ．
12. 如图，直线AB与半径为4的⊙O相切于点C ， 点D在⊙O上，连接CD ， DE ， 且∠EDC＝30°，弦EF∥AB ， 则EF的长为 ．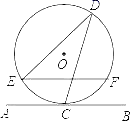
13. 如图，已知 是 的直径， 是 的切线，连接 交 于点 ，连接 ．若 ，则 的度数是 ．
14. 如图，为的切线，点A为切点，交于点C，点D在上，连接、 ， ， 若 ， 则的度数为.
15. 如图，已知半圆O与四边形ABCD的边AD、AB、BC都相切，切点分别为D、E、C，半径OC=2，则AE•BE=.
三、解答题
-
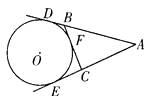
16. 如图，AE、AD、BC分别切⊙O于点E、D、F，若AD=20，求△ABC的周长．
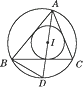
17. 如图，在△ABC中，I是△ABC的内心，∠BAC的平分线和△ABC的外接圆相交于点D.求证：DI=DB.
18. 如图，在Rt△ABC中，∠ABC=90°，∠BAC的平分线交BC于D，以D为圆心，DB为半径作☉D.求证：AC与☉D相切.
19. 平面上，矩形ABCD与直径为QP的半圆K如图1摆放，分别延长DA和QP交于点O，且∠DOQ=60°，OQ=OD=3，OP=2，OA=AB=1．让线段OD及矩形ABCD位置固定，将线段OQ连带着半圆K一起绕着点O按逆时针方向开始旋转，设旋转角为α（0°≤α≤60°）．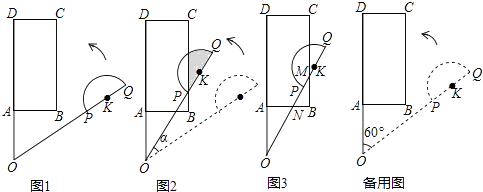
发现：如图2，当点P恰好落在BC边上时，求a的值即阴影部分的面积；
拓展：如图3，当线段OQ与CB边交于点M，与BA边交于点N时，设BM=x（x＞0），用含x的代数式表示BN的长，并求x的取值范围．
探究：当半圆K与矩形ABCD的边相切时，直接写出sinα的值．
20. 如图，AB是⊙O的直径，点C在⊙O上（异于A、B两点），AD⊥CD．①若BC=3，AB=5，求AC的长？
②若AC是∠DAB的平分线，求证：直线CD与⊙O相切．
