（华师大版）2022-2023学年九年级数学下册27.2.2直线与圆的位置关系 同步测试
试卷更新日期：2022-10-24 类型：同步测试
一、单选题
-
1. 如图，在 中， ， ， ，以点 为圆心，以 的长为半径作圆，则 与 的位置关系是（ ）
A、相交 B、相切 C、相离 D、相切或相离2. 已知⊙O的半径是5cm，点O到同一平面内直线a的距离为4cm，则直线a与⊙O的位置关系是（ ）A、相交 B、相切 C、相离 D、相交或相离3. 如图，两个同心圆，大圆的半径为5，小圆的半径为3，若大圆的弦AB与小圆有公共点，则弦AB的取值范围是（ ）
A、8≤AB≤10 B、8＜AB≤10 C、4≤AB≤5 D、4＜AB≤54. 已知⊙O的半径为6cm，圆心O到直线l的距离为5cm，则直线l与⊙O的交点个数为（ ）A、0 B、l C、2 D、无法确定5. 已知⊙O的半径r=3，设圆心O到一条直线的距离为d，圆上到这条直线的距离为2的点的个数为m，给出下列命题：①若d＞5，则m=0；②若d=5，则m=1；③若1＜d＜5，则m=3；④若d=1，则m=2；⑤若d＜1，则m=4.
其中正确命题的个数是（ ）
A、1 B、2 C、3 D、56. 已知△ABC中，AB=AC=6cm，BC=8cm，以点A为圆心，以4cm长为半径作圆，则⊙A与BC的位置关系是（ ）
A、相离 B、相切 C、相交 D、外离7. 已知圆O的圆心到直线L的距离为3，若圆上有且只有2个点到L的距离为2，则半径r的取值范围是（ ）A、r=3 B、1＜r＜3 C、1＜r＜5 D、1≤r≤58. 下列判断正确的是（ ）①直线上一点到圆心的距离大于半径，则直线与圆相离；②直线上一点到圆心的距离等于半径，则直线与圆相切；③直线上一点到圆心的距离小于半径，则直线与圆相交．
A、①②③ B、①② C、②③ D、③9. 已知☉O的半径为5，点P在直线l上，且OP=5，则直线l与☉O的位置关系是（ ）A、相切 B、相交 C、相离 D、相切或相交10. 如图，以点O为圆心的两个圆，半径分别为5和3，若大圆的弦AB与小圆相交，则弦AB的长度的取值范围是（ ）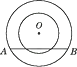
A、8≤AB≤10 B、AB≥8 C、8<AB≤10 D、8<AB<10二、填空题
-
11. 在矩形ABCD中，AB＝5，BC＝12，点A在⊙B上，如果⊙D与⊙B相切，那么⊙D的半径等于 ．
12. 已知 的半径为4cm，点P在直线l上，且点P到圆心O的距离为4cm，则直线l与 .13. 如图，已知∠BOA=30°，M为OA边上一点，以M为圆心、2cm为半径作⊙M.点M在射线OA上运动，当OM=5cm时，⊙M与直线OB的位置关系是.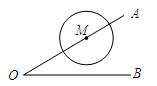
14. 如图，正方形ABCD的边长为8，M是AB的中点，P是BC边上的动点，连结PM，以点P为圆心，PM长为半径作⊙P．当⊙P与正方形ABCD的边相切时，BP的长为 ．
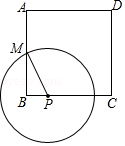15. 如图，在Rt△ABC中，∠C=90°，AC=3，BC=4，若以C为圆心，R为半径所作的圆与斜边AB有两个交点，则R的取值范围是 ．
三、解答题
-
16. 设⊙O的圆心O到直线的距离为d，半径为r，且直线与⊙O相切.d，r是一元二次方程（m+9）x2-（m+6）x+1=0的两根，求m的值.17. 如图，正方形ABCD的边长为2，AC和BD相交于点O，过O作EF∥AB，交BC于E，交AD于F，则以点B为圆心， 长为半径的圆与直线AC，EF，CD的位置关系分别是什么？
18. 如图，在直角坐标系中直线AB分别交x轴，y轴与A（﹣6，0）、B（0，﹣8）两点，现有一半径为1的动圆，圆心由A点，沿着AB方向以每秒1个单位的速度做平移运动，则经过几秒后动圆与坐标轴相切．
19. 设⊙O的圆心O到直线的距离为d，半径为r，且直线与⊙O相切．d，r是一元二次方程（m+9）x2﹣（m+6）x+1=0的两根，求m的值．20.如图，公路MN与公路PQ在点P处交汇，且∠QPN=30°，点A处有一所中学，AP=160m．假设拖拉机行驶时，周围100m以内会受到噪音的影响，那么拖拉机在公路MN上沿PN方向行驶时，学校是否受到噪音影响？说明理由；如果受影响，且知拖拉机的速度为18km/h，那么学校受影响的时间是多少秒？
21.如图，在平面直角坐标系xOy中，点A、B坐标分别为（4，2）、（0，2），线段CD在于x轴上，CD＝ ， 点C从原点出发沿x轴正方向以每秒1个单位长度向右平移，点D随着点C同时同速同方向运动，过点D作x轴的垂线交线段AB于点E、交OA于点G，连结CE交OA于点F．设运动时间为t，当E点到达A点时，停止所有运动．
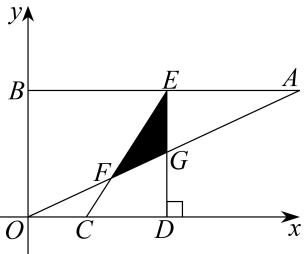
（1）求线段CE的长；
（2）记S为RtΔCDE与ΔABO的重叠部分面积，试写出S关于t的函数关系式及t的取值范围；
（3）连结DF，
①当t取何值时，有DF=CD?
②直接写出ΔCDF的外接圆与OA相切时t的值.
