（华师大版）2022-2023学年九年级数学下册27.2.1点与圆的位置关系 同步测试
试卷更新日期：2022-10-24 类型：同步测试
一、单选题
-
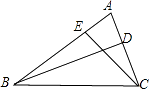
1. 如图，在正方形网格中，点 ， ， ， ， 都在格点上.下列说法正确的是（ ）
A、点 是 的内心 B、点 是 的外心 C、点 是 的内心 D、点 是 的外心2. 若⊙O的半径为5cm，点A到圆心O的距离为4cm，则点A与⊙O的位置关系是（ ）A、点A在圆外 B、点A在圆上 C、点A在圆内 D、不能确定3. 已知点O是 的外心，作正方形 ，下列说法：①点O是 的外心；②点O是 的外心；③点O是 的外心；④点O是 的外心.其中说法一定正确的是（ ）A、②④ B、①③ C、②③④ D、①③④4. 在 中， ， ，根据以下圆规作图的痕迹，只用无刻度直尺能符合题意找到 的外心的是（ ）A、
B、
C、
D、
5. 如图，抛物线 与 轴交于 两点， 是以点 为圆心， 为半径的圆上的动点， 是线段 的中点，连接 ，则线段 的最小值是（ ）
A、 B、 C、 D、6. 如图，在△ABC中，AB=13cm，AC=12cm，BC=5cm.D是BC边上的一个动点，连接AD，过点C作CE⊥AD于E，连接BE，在点D变化的过程中，线段BE的最小值是（ ）
A、2.5 B、 C、 D、57. 有下到结论：（1）三点确定一个圆；（2）平分弦的直径垂直于弦；（3）三角形的外心到三角形各边的距离相等，其中正确的结论的个数有（ ）A、0个 B、1个 C、2个 D、3个8. 若三角形的外心在这个三角形的一边上，则这个三角形是（ ）.A、锐角三角形 B、直角三角形 C、钝角三角形 D、不能确定9. 如图，在Rt△ABC中，∠A＝90°，AB＝6，AC＝8，点D为边BC的中点，点M为边AB上的一动点，点N为边AC上的一动点，且∠MDN＝90°，则sin∠DMN为（ ）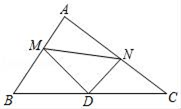
A、 B、 C、 D、10. 已知⊙O的半径为4，点P在⊙O内，则OP的长可能是（ ）A、3 B、4 C、5 D、6二、填空题
-
11. 如图，在△ABC中，AB＝AC，AD是BC边上的中线，分别以点A、C为圆心，以大于AC长为半径画弧，两弧相交于点EF，直线EF与AD交于点P，若PA＝2，则△ABC外接圆的面积为 ．
12. 我们发现：若AD是△ABC的中线，则有AB2+AC2＝2（AD2+BD2），请利用结论解决问题：如图，在矩形ABCD中，已知AB＝20，AD＝12，E是DC中点，点P在以AB为直径的半圆上运动，则CP2+EP2的最小值是.
13. 若的半径为5cm，点到圆心的距离为4cm，那么点与的位置关系是.14. 圆外一点到圆上点的最大距离是10cm，到圆上点的最小距离是2cm，则该圆的半径是cm.15. 如图，正方形ABCD的边长为4，P是边CD上的一动点，EF⊥BP交BP于G，且EF平分正方形ABCD的面积，则线段GC的最小值是.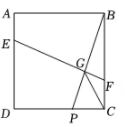
三、解答题
-
16. 以矩形ABCD的顶点A为圆心画⊙A，使得B、C、D中至少有一点在⊙A内，且至少有一点在⊙A外，若BC=12，CD=5.求⊙A的半径r的取值范围。17. 如图，在Rt△ABC中，∠ACB=90°，AC=BC=2，以BC为直径的半圆交AB于D，P是 上的一个动点，连接AP，求AP的最小值．
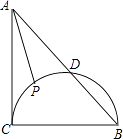18. 如图，有两条公路OM，ON相交成30°，沿公路OM方向离两条公路的交叉处O点80米的A处有一所希望小学，当拖拉机沿ON方向行驶时，路两旁50米内会受到噪音影响，已知有两台相距30米的拖拉机正沿ON方向行驶，它们的速度均为5米/秒，问这两台拖拉机沿ON方向行驶时给小学带来噪音影响的时间是多少？
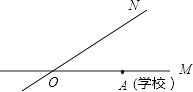19. 如图1，⊙O的半径为r（r＞0），若点P′在射线OP上，满足OP′•OP=r2 ， 则称点P′是点P关于⊙O的“美好点”．如图2，⊙O的半径为2，点B在⊙O上，∠BOA=60°，OA=4，若点A′、B′分别是点A，B关于⊙O的美好点，求A′B′的长．
20. 如图所示，BD，CE是△ABC的高，求证：E，B，C，D四点在同一个圆上．
