（华师大版）2022-2023学年九年级数学下册27.1.3圆周角 同步测试
试卷更新日期：2022-10-24 类型：同步测试
一、单选题
-
1. 如图，为直径， ，则的度数为（ ）
A、 B、 C、 D、2. 下列命题正确的个数有（ ）①直径是圆的对称轴；②平分弦的直径垂直于弦；③相等的圆周角所对的弧相等；④顶点在圆上的角是圆周角；⑤直径是弦；⑥半圆是弧
A、1个 B、2个 C、3个 D、4个3. 如图，中，AB边是圆O的直径，BC与圆O交于点D，且D是BC的中点， ， 点E在圆O上，则的度数是（ ）
A、70° B、60° C、50° D、40°4. 如图，在中，AB为直径，CD为弦，若 ， 则的度数是（ ）
A、40° B、50° C、60° D、70°5. 如图，AB是半圆O的直径，D为半圆上的点，在BA延长线上取点C，使得DC＝DO，连结CD并延长交圆O于点E，连结AE，若∠C＝18°，则∠EAB的度数为（ ）
A、18° B、21° C、27° D、36°6. 如图，扇形AOB的圆心角为124°，则∠ACB=（ ）
A、114° B、116° C、118° D、120°7. 如图，点A，B，C是上的三个点，若 ， 则的度数为（ ）
A、38° B、48° C、52° D、76°8. 如图，AB是⊙O的直径，CD是弦，若∠BCD=36°，则∠ABD等于（ ）
A、36° B、54° C、64° D、72°9. 如图，四边形ABCD中，对角线AC，BD交于点E，若∠BAC＝∠BDC，则下列结论中正确的是（ ）① ；②△ABE与△DCE的周长比 ；③∠ADE＝∠ABC；④S△ABE•S△DCE＝S△ADE•S△BCE.
A、③④ B、①②③ C、①②④ D、①②③④10. 我们定义：两边平方和等于第三边平方的2倍的三角形叫做奇异三角形，根据定义：①等边三角形一定是奇异三角形；②在Rt△ABC中，∠C＝90°，AB＝c，AC＝b，BC＝a，且b＞a，若Rt△ABC是奇异三角形，则a：b：c＝1：：2；③如图，AB是⊙O的直径，C是⊙O上一点（不与点A、B重合），D是半圆的中点，C、D在直径AB的两侧，若在⊙O内存在点E，使AE＝AD，CB＝CE．则△ACE是奇异三角形；④在③的条件下，当△ACE是直角三角形时，∠AOC＝120°，其中，说法正确的有（ ）
A、①② B、①③ C、②④ D、③④二、填空题
-
11. 如图，AB为⊙O的直径，点C，D在圆上，若∠D=64°，则∠BAC的度数为°.
12. 如图，在扇形AOB中， ， 点E在弧AB上，点F在OB上， ， 若 ， ， 则扇形AOB半径为.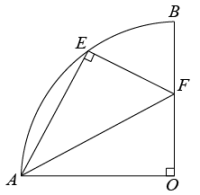
13. 如图，点A、B、C在⊙O上，∠ACB+∠AOB=90°，则∠ACB的大小为
14. 如图，已知⊙O是△ABD的外接圆，AB是⊙O的直径，CD是⊙O的弦，∠ABD＝56°，则∠BCD等于.
15. 如图，AB为圆O的直径，过点A的切线与弦BD的延长线相交于点C， ，若 ， ，则 .
三、解答题
-
16. 如图， 内接于 ，且 为直径，D为 上一点且 ，求证： 为等腰三角形.
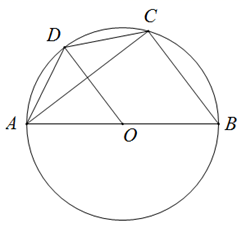17. 如图，在圆的内接四边形ABCD中，AB＝AD，BA、CD的延长线相交于点E，且AB＝AE，求证：BC是该圆的直径.
18. 已知：如图，△ABC的外接圆⊙O的直径为4，∠A=30°，求BC的长.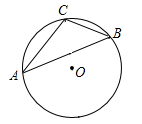
19. 如图，AB为半圆O的直径，弦AD、BC相交于点P，若CD=3，AB=4，求tan∠BPD的值.
20. 如图，在⊙O中，F，G是直径AB上的两点，C，D，E是半圆上的三点，如果弧AC的度数为60°，弧BE的度数为20°，∠CFA=∠DFB，∠DGA=∠EGB．求∠FDG的大小
