（华师大版）2022-2023学年九年级数学下册27.1.2圆的对称性 同步测试
试卷更新日期：2022-10-24 类型：同步测试
一、单选题
-
1. 如图，AB是的直径，弦 ， 垂足为E，如果 ， ， 那么线段BE的长为（ ）
A、4 B、6 C、8 D、92. 如图以CD为直径的⊙O中，弦AB⊥CD于M.AB=16，CM=16.则MD的长为（ ）
A、2 B、4 C、6 D、83. 《九章算术》是我国古代第一部自成体系的数学专著，书中记载：“今有圆材，埋在壁中，不知大小，以锯锯之，深两寸，锯道长八寸，问径几何？”译为：“今有一圆柱形木材，埋在墙壁中，不知其大小，用锯去锯这木材，锯口深2寸（ED＝2寸），锯道长8寸”，问这块圆形木材的直径是多少？”如图所示，请根据所学知识计算圆形木材的直径AC是（ ）
A、5寸 B、8寸 C、10寸 D、12寸4. 下列语句中：①平分弦的直径垂直于弦；②相等的圆心角所对的弧相等；③长度相等的两条弧是等弧；④圆是轴对称图形，任何一条直径都是它的对称轴；⑤在同圆或等圆中，如果两条弦相等，那么他们所对的圆周角相等，不正确的有（ ）A、2个 B、3个 C、4个 D、5个5. 如图，在平面直角坐标系中，半径为5的⊙E与y轴交于点A(0，-2)，B（0，4），与x轴交于C，D，则点D的坐标为（ ）
A、 B、 C、 D、6. 《九章算术》是我国古代数学成就的杰出代表，其中《方田》章给出计算弧田面积所用公式为：弧田面积＝ （弦×矢＋矢2），弧田（如图）是由圆弧和其所对的弦所围成，公式中“弦”指圆弧所对弦长AB，“矢”等于半径长与圆心O到弦的距离之差．在如图所示的弧田中，“弦”为8，“矢”为3，则cos∠OAB＝（ ）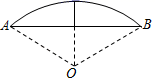
A、 B、 C、 D、7. 如图，CD为⊙O的直径，弦AB⊥CD，垂足为E，CE＝1，AB＝6，则⊙O的半径为（ ）
A、3 B、4 C、5 D、无法确定8. 一根排水管的截面如图所示，已知排水管的截面圆半径 ，截面圆圆心 到水面的距离 是6，则水面宽 是（ ）
A、16 B、10 C、8 D、69. 如图，AB是⊙O的直径，弦CD交AB于点P，AP=2，BP=6，∠APC=30°，则CD的长为（ ）
A、 B、2 C、2 D、810. 如图，⊙O 中弦AB =8，OC⊥AB，垂足为E，如果CE=2，那么⊙O的半径长是（ ）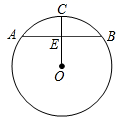
A、4 B、5 C、6 D、1°二、填空题
-
11. 如图，AB为⊙O的弦，半径OC⊥AB，垂足为D，如果AB＝8cm，CD＝2cm，那么⊙O的半径是cm.
12. 已知⊙的直径是4，⊙上两点、分⊙所得劣弧与优弧之比为1：3，则弦的长为.13. 已知：如图，AB是⊙O的直径，弦CD交AB于E点，BE＝1，AE＝5，∠AEC＝30°，则CD的长为 ．
14. 如图， 是圆 的直径， 与 交于点 ．如果 ，那么 的长为 ．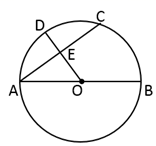
15. 已知 的半径为 ，弦 ，则圆心O到弦 的距离是 ．三、解答题
-
16. 如图，AB是 的直径，弦 于点E，若 ， ，求 的长．
17. 已知AB，AC为弦，OM⊥AB于M，ON⊥AC于N，求证：MN∥BC且MN＝ BC．
18. 某地出土一个明代残破圆形瓷盘，为复制该瓷盘需确定其圆心和半径，请在图中用直尺和圆规画出瓷盘的圆心（不要求写作法、证明和讨论，但要保留作图痕迹）
19. 如图，⊙O的半径为17cm，弦AB∥CD，AB=30cm，CD=16cm，圆心O位于AB，CD的上方，求AB和CD的距离.
20. 如图，将一个两边都带有刻度的直尺放在半圆形纸片上，使其一边经过圆心O，另一边所在直线与半圆相交于点D，E，量出半径OC=5cm，弦DE=8cm，求直尺的宽．
21. ⊙O的直径为10，弦AB的长为8，P是弦AB上的一个动点，求OP长的取值范围.思路分析：求出OP长的最小值和最大值即得范围，本题考查垂径定理及勾股定理.该题创新点在于把线段OP看作是一个变量，在动态中确定OP的最大值和最小值.事实上只需作OM⊥AB，求得OM即可.
