（华师大版）2022-2023学年九年级数学下册第26章二次函数单元测试

试卷更新日期：2022-10-24 类型：单元试卷

进入出卷网下载

一、单选题

1. 下列函数中，属于二次函数的是（）

A、y= $\frac{2}{x}$ B、y=2（x+1）（x﹣3） C、y=3x﹣2 D、y=

查看试题解析
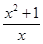2. 函数y=（m﹣3）x^|m|^﹣1+3x﹣1是二次函数，则m的值是（　　）

A、-3 B、3 C、±2 D、±3

查看试题解析
3. 长方形的周长为24cm，其中一边为xcm（其中x＞0），面积为ycm² ，则这样的长方形中y与x的关系可以写为（　　）

A、y=x² B、y=12﹣x² C、y=（12﹣x）•x D、y=2（12﹣x）

查看试题解析
4. 已知二次函数 $y = a x^{2} + b x + c$ 的图象如图所示，下列结论，正确的有（）个
① $a b c > 0$ ② $2 a - b < 0$ ③ $4 a - 2 b + c < 0$ ④ ${(a + c)}^{2} > b^{2}$

A、1个 B、2个 C、3个 D、4个

查看试题解析
5. 将抛物线 $y = 3 x^{2}$ 向左平移2个单位，再向下平移1个单位，所得抛物线为（）

A、 $y = 3 {(x - 2)}^{2} - 1$ B、 $y = 3 {(x - 2)}^{2} + 1$ C、 $y = 3 {(x + 2)}^{2} - 1$ D、 $y = 3 {(x + 2)}^{2} + 1$

查看试题解析
6. 二次函数y=（x-3）²+1的最小值是（）

A、3 B、-3 C、1 D、-1

查看试题解析
7. 关于x的方程ax²+bx+c＝0有两个不相等的实根x₁ ， x₂ ，若x₂＝2x₁ ，则4b﹣3ac的最大值是（）

A、1 B、2 C、4 D、6

查看试题解析
8. 如图，抛物线与x轴交于点（﹣1，0）和（3，0），与y轴交于点（0，﹣3）则此抛物线对此函数的表达式为（）

A、y=x²+2x+3 B、y=x²﹣2x﹣3 C、y=x²﹣2x+3 D、y=x²+2x﹣3

查看试题解析
9. 如图是二次函数 $y = a x^{2} + b x + c$ 图象的一部分，图象过点 $A (- 3 ， 0)$ ，对称轴为直线 $x = - 1$ ，给出以下结论：① $a b c < 0$ ；② $b^{2} - 4 a c > 0$ ；③ $4 b + c < 0$ ；④若 $B (- \frac{5}{2} ， y_{1}) 、 C (- \frac{1}{2} ， y_{2})$ 为函数图象上的两点，则 $y_{1} > y_{2}$ ；⑤当 $- 3 \leq x \leq 1$ 时， $y \geq 0$ ，其中正确的结论有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
10. 已知函数 $y = k x^{2} - 7 x - 7$ 的图象与 $x$ 轴有交点，则 $k$ 的取值范围是（）

A、 $k > - \frac{7}{4}$ B、 $k \geq - \frac{7}{4} 且 k \neq 0$ C、 $k \geq - \frac{7}{4}$ D、 $k > - \frac{7}{4} 且 k \neq 0$

查看试题解析

二、填空题

11. 若函数y=（m﹣1）x^|^m^|+¹是二次函数，则m的值为．

查看试题解析
12. 如图所示，在同一坐标系中，作出①y=a₁x² ， ②y=a₂x² ， ③y=a₃x²的图象，比较a₁、a₂、a₃大小是．

查看试题解析
13. 抛物线 $y = a x^{2} + 3 x - 1$ 的顶点在x轴上，那么 $a =$ .

查看试题解析
14. 已知一个二次函数的图象开口向上，顶点坐标为（0，﹣1 ），那么这个二次函数的解析式可以是．（只需写一个）

查看试题解析
15. 抛物线 $y = (a^{2} + 2) x^{2} + b x + c$ 经过点 $A (- 1 ， t)$ ， $B (5 ， t)$ 两点，则不等式 $(a^{2} + 2) {(x + 3)}^{2} + b x > - 3 b - c + t$ 的解集是.

查看试题解析

三、解答题

16.
把8米长的钢筋，焊成一个如图所示的框架，使其下部为矩形，上部为半圆形．请你写出钢筋所焊成框架的面积y（平方米）与半圆的半径x（米）之间的函数关系式．

查看试题解析
17. 如图，一块矩形草地的长为100m，宽为80m，欲在中间修筑两条互相垂直的宽为x（m）的小路，这时草坪的面积为y（m²）．求y与x的函数关系式，并求出x的取值范围．

查看试题解析
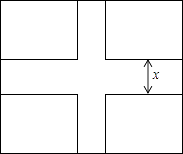18.
如图①，正方形ABCD中，点A、B的坐标分别为（0，10），（8，4），点C在第一象限．动点P在正方形ABCD的边上，从点A出发沿A⇒B⇒C⇒D匀速运动，同时动点Q以相同速度在x轴正半轴上运动，当P点到达D点时，两点同时停止运动，设运动的时间为t秒．

（1）当P点在边AB上运动时，点Q的横坐标x（长度单位）关于运动时间t（秒）的函数图象如图②所示，请写出点Q开始运动时的坐标及点P运动速度；
（2）求正方形边长及顶点C的坐标；
（3）如果点P、Q保持原速度不变，当点P沿A⇒B⇒C⇒D匀速运动时，OP与PQ能否相等？若能，求出所有符合条件的t的值；若不能，请说明理由．

查看试题解析
19.
已知：把Rt△ABC和Rt△DEF按如图（1）摆放（点C与点E重合），点B、C（E）、F在同一条直线上．∠ACB = ∠EDF = 90°，∠DEF = 45°，AC =" 8" cm，BC =" 6" cm，EF =" 9" cm．
如图（2），△DEF从图（1）的位置出发，以1 cm/s的速度沿CB向△ABC匀速移动，在△DEF移动的同时，点P从△ABC的顶点B出发，以2 cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时，△DEF停止移动，点P也随之停止移动．DE与AC相交于点Q，连接PQ，设移动时间为t（s）（0＜t＜4.5）．

解答下列问题：
（1）当t为何值时，点A在线段PQ的垂直平分线上？
（2）连接PE，设四边形APEC的面积为y（cm2），求y与t之间的函数关系式；是否存在某一时刻t，使面积y最小？若存在，求出y的最小值；若不存在，说明理由．
（3）是否存在某一时刻t，使P、Q、F三点在同一条直线上？若存在，求出此时t的值；若不存在，说明理由．

查看试题解析
20.
如图，矩形ABCD中，AB=16cm，AD=4cm，点P、Q分别从A、B同时出发，点P在边AB上沿AB方向以2cm/s的速度匀速运动，点Q在边BC上沿BC方向以1cm/s的速度匀速运动，当其中一点到达终点时，另一点也随之停止运动.设运动时间为x秒，△PBQ的面积为y（cm²）.

（1）求y关于x的函数关系式，并写出x的取值范围；
（2）求△PBQ的面积的最大值.

查看试题解析
21. 根据条件求二次函数的解析式：

(1)、抛物线的顶点坐标为（﹣1，﹣1），且与y轴交点的纵坐标为﹣3

(2)、抛物线在x轴上截得的线段长为4，且顶点坐标是（3，﹣2）．

查看试题解析
22. 在平面直角坐标系xOy中，抛物线y＝mx²－2mx＋m－1(m＞0)与x轴的交点为A，B，顶点为C，将抛物线在A，C，B之间的部分记为图象E(A，B两点除外)．

(1)、求抛物线的顶点坐标．

(2)、AB＝6时，经过点C的直线y＝kx＋b(k≠0)与图象E有两个交点，结合函数的图象，求k的取值范围．

(3)、若横、纵坐标都是整数的点叫整点．
①当m＝1时，求线段AB上整点的个数；
②若抛物线在点A，C，B之间的图象E与线段AB所围成的区域内(包括边界)恰有6个整点，结合函数的图象，求m的取值范围．

查看试题解析
23. 已知二次函数y=kx²﹣（2k+1）x+（k+1）（k≠0为实数）．
（1）求证：不论k为何值，该函数的图象与x轴总有两个公共点；
（2）该函数的图象与x轴交于A、B两点，与y轴交于点C．
①当△ABC的面积等于2时，求k的值；
②对任意负实数a＜0，当x＞m时，y随着x的增大而减小，试求出m的一个值．

查看试题解析

（华师大版）2022-2023学年九年级数学下册第26章 二次函数 单元测试

一、单选题

二、填空题

三、解答题

（华师大版）2022-2023学年九年级数学下册第26章二次函数单元测试