（华师大版）2022-2023学年九年级数学下册26.2.2 二次函数y=ax2+bx+c 同步测试

试卷更新日期：2022-10-24 类型：同步测试

进入出卷网下载

一、单选题

1. 抛物线y＝﹣2（x﹣3）²﹣4的顶点坐标是（　　）

A、（﹣3，4） B、（﹣3，﹣4） C、（3，﹣4） D、（3，4）

查看试题解析
2. 若关于x的方程x²＋2mx＋m²＋3m－2＝0有两个实数根x₁、x₂ ，则x₁（x₂＋x₁）＋x₂²的最小值为（）

A、 $\frac{5}{4}$ B、 $\frac{2}{3}$ C、 $\frac{1}{2}$ D、－2

查看试题解析
3. 已知二次函数y＝ax²+bx+c的图象过点A（2，n），当x＞0时，y≥n，当x≤0时，y≥n+1，则a的值是（）

A、﹣1 B、﹣ $\frac{1}{4}$ C、 $\frac{1}{4}$ D、1

查看试题解析
4. 二次函数y＝x（x+2）图象的对称轴是（）

A、x＝﹣1 B、x＝﹣2 C、x＝2 D、y轴

查看试题解析
5. 通过平移y=−2(x−1)²+3的图象，可得到y=−2x²的图象，下列平移方法正确的是（）

A、向左移动1个单位，向上移动3个单位 B、向右移动1个单位，向上移动3个单位 C、向左移动1个单位，向下移动3个单位 D、向右移动1个单位，向下移动3个单位

查看试题解析

6. 二次函数y＝ax²+bx+c的自变量x和函数y的部分对应值如表：

x	…	0	$\frac{1}{2}$	1	2	3	4	…
y	…	4	5	4	﹣4	﹣20	﹣45	…

则该二次函数y在所给自变量x（﹣2≤x≤2）的取值范围内的最小值是（）

A、﹣45 B、﹣20 C、﹣4 D、0

查看试题解析

7. 将抛物线y＝ $\frac{1}{2}$ x²的图象向左平移2个单位，所得到的抛物线表达式为（）

A、y＝ $\frac{1}{2}$ （x+2）² B、y＝ $\frac{1}{2}$ （x﹣2）² C、y＝ $\frac{1}{2}$ x²+2 D、y＝ $\frac{1}{2}$ x²﹣2

查看试题解析
8. 当0≤x≤m时，函数y=-x²+4x-3的最小值为-3，最大值为1，则m的取值范围是（）

A、-1≤m≤0 B、2≤m< $\frac{7}{2}$ C、2≤m≤4 D、 $\frac{9}{4}$ <m≤ $\frac{7}{2}$

查看试题解析
9. 若抛物线 $y = a x^{2} + 2 x + 1$ 只经过三个象限，则a的取值范围是（）

A、 $a < 1$ B、 $a \leq 1$ C、 $0 < a < 1$ D、 $0 < a ⩽ 1$

查看试题解析
10. 抛物线y＝2（x﹣1）²﹣ $\frac{1}{2}$ 的顶点坐标为（）

A、（1，﹣ $\frac{1}{2}$ ） B、（﹣1，﹣ $\frac{1}{2}$ ） C、（﹣1， $\frac{1}{2}$ ） D、（1， $\frac{1}{2}$ ）

查看试题解析

二、填空题

11. 若把函数y=x的图象用E(x，x)记，函数y=2x+1的图象用E（x，2x+1）记，……则E(x， $x^{2} - 2 x + 3$ )图象上的最低点是.

查看试题解析
12. 抛物线 $y = - 2 {(x + 2)}^{2} + 5$ 的顶点坐标是．

查看试题解析
13. 如果抛物线 $y = 3 x^{2}$ 向下平移2个单位，所得到的抛物线是．

查看试题解析
14. 二次函数 $y = x^{2} - 2 x + 4$ 的最小值为．

查看试题解析

15. 已知二次函数

y = x^{2} + bx + c

，函数y与自变量x的部分对应值如下表：

则当y＜5时，x的取值范围是.

x	…	-1	0	1	2	3	…
y	…	10	5	2	1	2	…

查看试题解析

三、解答题

16. 已知抛物线y=mx²+n向下平移2个单位后得到的函数图象是y=3x²﹣1，求m、n的值．

查看试题解析
17. 求二次函数y=﹣2x²+8x﹣6的对称轴、顶点坐标．

查看试题解析
18. 已知直角三角形的两直角边的和为2，求斜边长的最小值，以及当斜边长达到最小值时的两条直角边的长．

查看试题解析
19. 将长为156cm的铁线剪成两段，每段都围成一个边长为整数（cm）的正方形，求这两个正方形面积和的最小值．

查看试题解析
20. 如图，设点P是边长为a的正三角形ABC的边BC上一点，过点P作PQ⊥AB，垂足为Q，延长QP交AC的延长线于点R．当点P在何处时，△BPQ与△CPR的面积之和取最大（小）值？并求出最大（小）值．

查看试题解析
21.
如图所示，在平面直角坐标系中，Rt△OBC的两条直角边分别落在x轴、y轴上，且OB=1，OC=3，将△OBC绕原点O顺时针旋转90°得到△OAE，将△OBC沿y轴翻折得到△ODC，AE与CD交于点F.

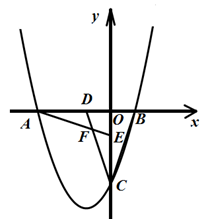
（1）若抛物线过点A、B、C，求此抛物线的解析式；
（2）求△OAE与△ODC重叠的部分四边形ODFE的面积；
（3）点M是第三象限内抛物线上的一动点，点M在何处时△AMC的面积最大？最大面积是多少？求出此时点M的坐标.

查看试题解析
22.
如图，在平行四边形ABCD中，AB=5，BC=10，F为AD的中点，CE⊥AB于E，设∠ABC=α（60°≤α＜90°）．

（1）当α=60°时，求CE的长；
（2）当60°＜α＜90°时，
①是否存在正整数k，使得∠EFD=k∠AEF？若存在，求出k的值；若不存在，请说明理由．
②连接CF，当CE²-CF²取最大值时，求tan∠DCF的值．

查看试题解析
23.
如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm．动点M，N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A，B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM，PN，设移动时间为t（单位：秒，0＜t＜2.5）．

（1）当t为何值时，以A，P，M为顶点的三角形与△ABC相似？
（2）是否存在某一时刻t，使四边形APNC的面积S有最小值？若存在，求S的最小值；若不存在，请说明理由．

查看试题解析