（浙教版）2022-2023学年九年级数学下册第二章 直线与圆的位置关系 单元测试
试卷更新日期：2022-10-24 类型：单元试卷
一、单选题（每题3分，共30分）
-
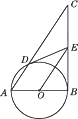
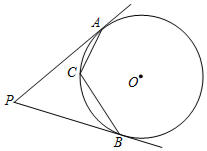
1. 如图，PA、PB分别与⊙O相切于A、B，∠P＝70°，C为⊙O上一点，则∠ACB的度数为（ ）
A、110° B、120° C、125° D、130°2. 已知⊙O的直径AB与弦AC的夹角为25°，过点C作⊙O的切线交AB的延长线于点D，则∠D等于（ ）
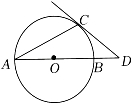A、25° B、30° C、35° D、40°3. 在同一平面内，有一半径为6的 和直线 ，直线 上有一点 ，且 ；则直线 与 的位置关系是（ ）A、相交 B、相离 C、相切 D、不能确定4. 如图，△ABC是⊙O的内接三角形，∠C＝70°，过点A的圆的切线交射线BO于点P ， 则∠P的度数是（ ）
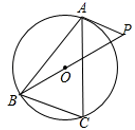A、40° B、45° C、50° D、60°5. 如图，AB是⊙0的直径，点C为⊙0外一点，CA，CD分别与⊙0相切于点A，点D，连结BD，AD，若∠ACD＝50°，则∠DBA的度数是（ ）
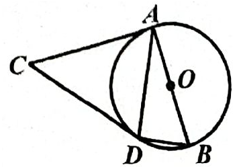A、15° B、35° C、65° D、75°6. 如图，PA，PB为⊙O的两条切线，点A，B是切点，OP交⊙O于点C，交弦AB于点D.下列结论中错误的是（ ）
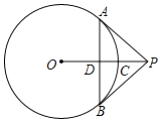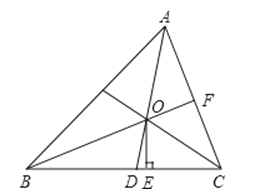
A、PA＝PB B、AD＝BD C、OP⊥AB D、∠PAB＝∠APB7. 如图，一圆内切四边形ABCD，且BC=10，AD=7，则四边形的周长为（ ）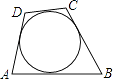
A、32 B、34 C、36 D、388. 如图，在△ABC中，∠BAC的平分线AD与∠ACB的平分线CE交于点O，下列说法正确的是（ ）
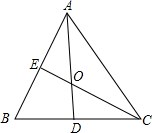A、点O是△ABC的内切圆的圆心 B、CE⊥AB C、△ABC的内切圆经过D，E两点 D、AO＝CO9. 如图，在△ABC中，AB＝10，AC＝8，BC＝6.按以下步骤作图：①以A为圆心，任意长为半径作弧，分别交AB，AC于点M，N；
②分别以M，N为圆心，以大于 MN的长为半径作弧，两弧交于点E；
③作射线AE；
④以同样的方法作射线BF，AE交BF于点O，连结OC，则OC为（ ）
A、2 B、2 C、 D、110. 如图在Rt△ABC中，∠ACB=90°，AC=6，BC=8，⊙O是△ABC的内切圆，连接AO，BO，则图中阴影部分的面积之和为（ ）
A、 B、 C、12 D、14二、填空题（每题3分，共15分）
-
11. 如图，AB是⊙O的弦，AC与⊙O相切于点A，接OA，OB，若∠P＝50°，则∠BAC＝.
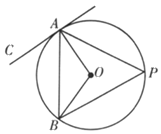12. 如图，⊙O的半径为4，AB为⊙O的直径，∠ABC=90°，直线CE与⊙O相切于点D，交BA的延长线于点E，A为OE的中点，则AC的长是.
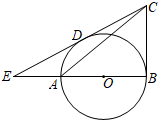13. 如图，直线PA过半圆的圆心O，交半圆于A，B两点，PC切半圆与点C，已知PC=3，PB=1，则该半圆的半径为 ．
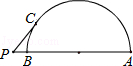14. 如图，等边△ABC中，P为三角形内一点，过P作PD⊥BC，PE⊥AB，PF⊥AC，连结AP、BP、CP，如果S△APF＋S△BPE＋S△PCD＝ ，那么△ABC的内切圆半径为
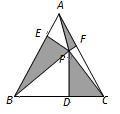15. 如图，△ABC，AC=3，BC=4，∠C=90°，⊙O为△ABC的内切圆，与三边的切点分别为D、E、F，则⊙O的面积为（结果保留π）
三、解答题（共8题，共55分）
-
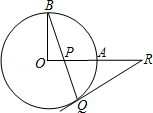
16. 如图，OA和OB是⊙O的半径，并且OA⊥OB，P是OA上任一点，BP的延长线交⊙O于Q，过Q的⊙O的切线交OA的延长线于R．求证：RP=RQ．
17. 如图，⊙O的半径为3cm，弦AC=4 cm，AB=4cm，若以O为圆心，再作一个圆与AC相切，则这个圆的半径为多少？这个圆与AB的位置关系如何？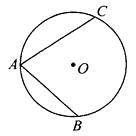
18. 如图，点O为∠MPN的平分线上一点，以点O为圆心的☉O与PN相切于点A.求证：PM为☉O的切线.
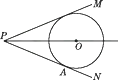19. 如图，☉O与四边形ABCD的四边都相切.若∠AOB=70°，求∠COD的度数.
20. 如图，以Rt△ABC的直角边AB为直径作☉O，与斜边AC交于点D，过点D作☉O的切线交BC边于点E.求证：EB=EC=ED
