(浙教版)2022-2023学年九年级数学下册2.3 三角形的内切圆 同步测试
试卷更新日期:2022-10-24 类型:同步测试
一、单选题 (每题3分,共30分)
-
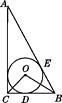
1. 如图,在 中, , 于D,⊙O为 的内切圆,设⊙O的半径为R,AD的长为h,则 的值为( )
 A、 B、 C、 D、2. 如图,在△ABC中,∠A=50°,内切圆I与边BC、CA、AB分别相切于点D、E、F,则∠EDF的度数为( )
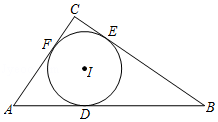
A、 B、 C、 D、2. 如图,在△ABC中,∠A=50°,内切圆I与边BC、CA、AB分别相切于点D、E、F,则∠EDF的度数为( )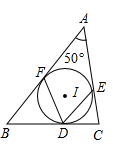 A、55° B、60° C、65° D、70°3. 已知三角形的周长为12,面积为6,则该三角形内切圆的半径为( )A、4 B、3 C、2 D、14. 如图,⊙O是△ABC的内切圆,切点分别相为点D、E、F,设△ABC的面积、周长分别为S、l,⊙O的半径为r,则下列等式:
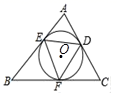
A、55° B、60° C、65° D、70°3. 已知三角形的周长为12,面积为6,则该三角形内切圆的半径为( )A、4 B、3 C、2 D、14. 如图,⊙O是△ABC的内切圆,切点分别相为点D、E、F,设△ABC的面积、周长分别为S、l,⊙O的半径为r,则下列等式:①∠AED+∠BFE+∠CDF=180°;②S=l r;③2∠EDF=∠A+∠C;④2(AD+CF+BE)=l,其中成立的是( )
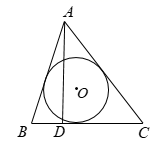
 A、①②③④ B、②③④ C、①③④ D、①②③5. 如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )
A、①②③④ B、②③④ C、①③④ D、①②③5. 如图,点O是△ABC的内心,若∠A=70°,则∠BOC的度数是( )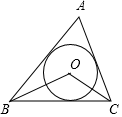 A、120° B、125° C、130° D、135°6. 根据尺规作图的痕迹,可以判定点O为 内心的是( )A、
A、120° B、125° C、130° D、135°6. 根据尺规作图的痕迹,可以判定点O为 内心的是( )A、 B、
B、 C、
C、 D、
D、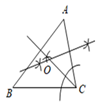 7. 如图,弓形 中, , .若点 在优弧 上由点 移动到点 ,记 的内心为 ,点 随点 的移动所经过的路径长为( ).
7. 如图,弓形 中, , .若点 在优弧 上由点 移动到点 ,记 的内心为 ,点 随点 的移动所经过的路径长为( ).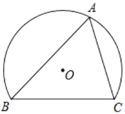 A、 B、 C、 D、8. 如图,正三角形的内切圆半径为1,那么这个正三角形的边长为( )
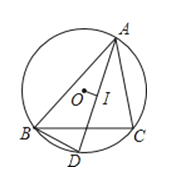
A、 B、 C、 D、8. 如图,正三角形的内切圆半径为1,那么这个正三角形的边长为( ) A、2 B、3 C、 D、9. 如图,在△ABC中,AC=BC,E是内心,AE的延长线交△ABC的外接圆于点D,以下四个结论:①BE=AE;②CE⊥AB;③△DEB是等腰三角形;④ .其中正确的个数是( )
A、2 B、3 C、 D、9. 如图,在△ABC中,AC=BC,E是内心,AE的延长线交△ABC的外接圆于点D,以下四个结论:①BE=AE;②CE⊥AB;③△DEB是等腰三角形;④ .其中正确的个数是( ) A、1个 B、2个 C、3个 D、4个10. 如图在Rt△ABC中,∠ACB=90°,AC=6,BC=8,⊙O是△ABC的内切圆,连接AO,BO.则图中阴影部分的面积之和( )
A、1个 B、2个 C、3个 D、4个10. 如图在Rt△ABC中,∠ACB=90°,AC=6,BC=8,⊙O是△ABC的内切圆,连接AO,BO.则图中阴影部分的面积之和( )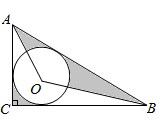
A、 B、 C、12 D、14二、填空题(每题3分,共15分)
-
11. 如图,△ABC的内切圆与三边分别切于点D,E,F,若∠C=90°,AD=3,BD=5,则△ABC的面积为.
 12. 如图,在 中, , , , 为 的内切圆,点D是斜边AB的中点,则 .
12. 如图,在 中, , , , 为 的内切圆,点D是斜边AB的中点,则 .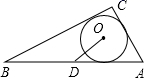 13. 已知一个直角三角形的两条直角边分别是6和8,则此直角三解形的内切圆半径r=.14. 已知一个直角三角形的两条直角边长分别为3cm和4cm,则这个直角三角形的内切圆的半径为cm15. 若一三角形的三边长分别为5、12、13,则此三角形的内切圆半径为.
13. 已知一个直角三角形的两条直角边分别是6和8,则此直角三解形的内切圆半径r=.14. 已知一个直角三角形的两条直角边长分别为3cm和4cm,则这个直角三角形的内切圆的半径为cm15. 若一三角形的三边长分别为5、12、13,则此三角形的内切圆半径为.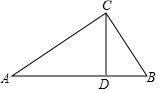
三、解答题(共8题,共55分)
-
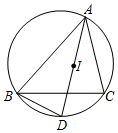
16. 如图,I是△ABC的内心,AI的延长线交△ABC的外接圆于点D.DB与DI相等吗?为什么?
 17. 已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长.
17. 已知:如图,⊙O内切于△ABC,∠BOC=105°,∠ACB=90°,AB=20cm.求BC、AC的长.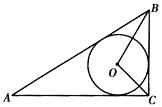 18. 已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.
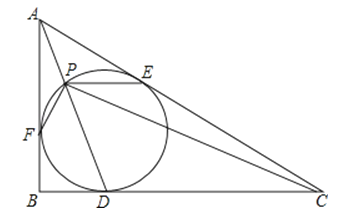
18. 已知:如图,△ABC三边BC=a,CA=b,AB=c,它的内切圆O的半径长为r.求△ABC的面积S.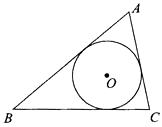 19. 如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC= 12,∠P=60°,求弦AB的长.
19. 如图,PA、PB是⊙O的两条切线,切点分别为点A、B,若直径AC= 12,∠P=60°,求弦AB的长.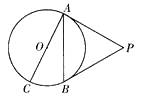 20. 如图,在Rt△ABC中,∠ACB=90°,☉O是Rt△ABC的内切圆,其半径为1,E,D是切点,∠BOC=105°.求AE的长.
20. 如图,在Rt△ABC中,∠ACB=90°,☉O是Rt△ABC的内切圆,其半径为1,E,D是切点,∠BOC=105°.求AE的长.