2022年秋季北师版数学九年级上学期期中复习检测B
试卷更新日期:2022-10-24 类型:期中考试
一、单选题(每题3分,共30分)
-
1. 下列说法错误的是( )A、对角线垂直且互相平分的四边形是菱形 B、同圆或等圆中,同弧对应的圆周角相等 C、对角线相等的四边形是矩形 D、对角线垂直且相等的平行四边形是正方形2. 为了疫情防控,某小区需要从甲、乙、丙、丁 4名志愿者中随机抽取2名负责该小区入口处的测温工作,则甲被抽中的概率是( )A、 B、 C、 D、3. 如图,在 中, ,则 的值是( )
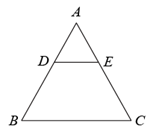 A、 B、 C、 D、4. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、5. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )
A、 B、 C、 D、4. 用配方法解一元二次方程 ,配方正确的是( ).A、 B、 C、 D、5. 如图,点 , 将线段平移得到线段 , 若 , 则点D的坐标是( )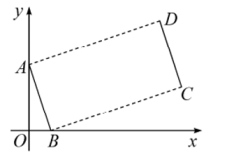 A、 B、 C、 D、6. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )
A、 B、 C、 D、6. 如图,正方形ABCD的面积为3,点E在边CD上, 且CE = 1,∠ABE的平分线交AD于点F,点M,N分别是BE,BF的中点,则MN的长为( )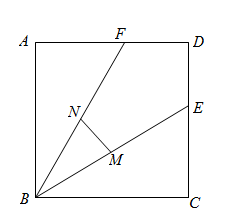 A、 B、 C、 D、7. 如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE + PF的最小值是( )
A、 B、 C、 D、7. 如图,菱形ABCD的边长为2,点P是对角线AC上的一个动点,点E、F分别为边AD、DC的中点,则PE + PF的最小值是( ) A、2 B、 C、1.5 D、8. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点.下列结论:①;②平分;③ , 其中所有正确结论的序号是( )
A、2 B、 C、1.5 D、8. 如图,在中, , 将以点为中心逆时针旋转得到 , 点在边上,交于点.下列结论:①;②平分;③ , 其中所有正确结论的序号是( )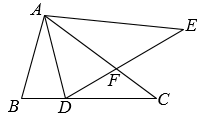 A、①② B、②③ C、①③ D、①②③9. 若关于x的一元二次方程有两个实数根 , , 且 , 则( )A、2或6 B、2或8 C、2 D、610. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )
A、①② B、②③ C、①③ D、①②③9. 若关于x的一元二次方程有两个实数根 , , 且 , 则( )A、2或6 B、2或8 C、2 D、610. 如图,在平面直角坐标系中,矩形ABCD的顶点A在第一象限,B,D分别在y轴上,AB交x轴于点E,轴,垂足为F.若 , . 以下结论正确的个数是( )①;②AE平分;③点C的坐标为;④;⑤矩形ABCD的面积为 .
 A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题(每题3分,共18分)
-
11. 2022年3月12日是我国第44个植树节,某林业部门为了考察某种幼树在一定条件下的移植成活率,在同等条件下,对这种幼树进行大量移植,并统计成活情况,下表是这种幼树移植过程中的一组统计数据:
幼树移植数(棵)
100
1000
5000
8000
10000
15000
20000
幼树移植成活数(棵)
87
893
4485
7224
8983
13443
18044
幼树移植成活的频率
0.870
0.893
0.897
0.903
0.898
0.896
0.902
估计该种幼树在此条件下移植成活的概率是 . (结果精确到0.1)
12. 如图,矩形的对角线 , 相交于点 , // , //.若 , 则四边形的周长是. 13. 如图,折叠边长为4cm的正方形纸片 , 折痕是 , 点落在点处,分别延长、交于点、 , 若点是边的中点,则cm.
13. 如图,折叠边长为4cm的正方形纸片 , 折痕是 , 点落在点处,分别延长、交于点、 , 若点是边的中点,则cm. 14. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).
14. 将一个容积为360cm3的包装盒剪开铺平,纸样如图所示.利用容积列出图中x(cm)满足的一元二次方程:(不必化简).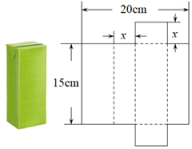 15. 如图,在矩形纸片ABCD中,点E在BC边上,将 沿DE翻折得到 ,点F落在AE上.若 , ,则 cm.
15. 如图,在矩形纸片ABCD中,点E在BC边上,将 沿DE翻折得到 ,点F落在AE上.若 , ,则 cm.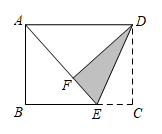 16. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .
16. 如图,菱形的对角线相交于点O,点E在上,连接 , 点F为的中点,连接 , 若 , , , 则线段的长为 .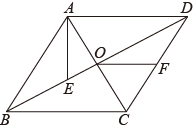
三、解答题(共9题,共72分)
-
17. 解方程: .18. 用配方法解方程: .19. 为扎实推进“五育并举”工作,某校利用课外活动时间开设了舞蹈、篮球、围棋和足球四个社团活动,每个学生只选择一项活动参加.为了解活动开展情况,学校随机抽取部分学生进行调查,将调查结果绘成如下表格和扇形统计图.
参加四个社团活动人数统计表
社团活动
舞蹈
篮球
围棋
足球
人数
50
30
80
参加四个社团活动人数扇形统计图

请根据以上信息,回答下列问题:
(1)、抽取的学生共有人,其中参加围棋社的有人;(2)、若该校有3200人,估计全校参加篮球社的学生有多少人?(3)、某班有3男2女共5名学生参加足球社,现从中随机抽取2名学生参加学校足球队,请用树状图或列表法说明恰好抽到一男一女的概率.20. 如图,在中,交于点 , 点在上, .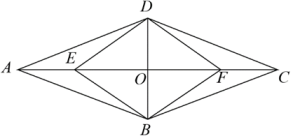 (1)、求证:四边形是平行四边形;(2)、若求证:四边形是菱形.21. 如图,四边形为菱形,点E在的延长线上, .
(1)、求证:四边形是平行四边形;(2)、若求证:四边形是菱形.21. 如图,四边形为菱形,点E在的延长线上, . (1)、求证:;(2)、当时,求的长.22. 列方程(组)解应用题
(1)、求证:;(2)、当时,求的长.22. 列方程(组)解应用题端午节期间,某水果超市调查某种水果的销售情况,下面是调查员的对话:
小王:该水果的进价是每千克22元;
小李:当销售价为每千克38元时,每天可售出160千克;若每千克降低3元,每天的销售量将增加120千克.
根据他们的对话,解决下面所给问题:超市每天要获得销售利润3640元,又要尽可能让顾客得到实惠,求这种水果的销售价为每千克多少元?
23. 综合与实践(1)、问题情境:在Rt△ABC中,∠BAC=90°,AB=6,AC=8.直角三角板EDF中∠EDF=90°,将三角板的直角顶点D放在Rt△ABC斜边BC的中点处,并将三角板绕点D旋转,三角板的两边DE,DF分别与边AB,AC交于点M,N,猜想证明:
如图①,在三角板旋转过程中,当点M为边AB的中点时,试判断四边形AMDN的形状,并说明理由;
(2)、问题解决:如图②,在三角板旋转过程中,当时,求线段CN的长;
(3)、如图③,在三角板旋转过程中,当AM=AN时,直接写出线段AN的长.24. 阅读材料,解答问题:材料1
为了解方程 , 如果我们把看作一个整体,然后设 , 则原方程可化为 , 经过运算,原方程的解为 , . 我们把以上这种解决问题的方法通常叫做换元法.
材料2
已知实数m,n满足 , , 且 , 显然m,n是方程的两个不相等的实数根,由书达定理可知 , .
根据上述材料,解决以下问题:
(1)、直接应用:方程的解为;
(2)、间接应用:已知实数a,b满足: , 且 , 求的值;
(3)、拓展应用:已知实数m,n满足: , 且 , 求的值.
25. 如图,在矩形ABCD中,AB=6,BC=4,点M、N分别在AB、AD上,且MN⊥MC,点E为CD的中点,连接BE交MC于点F. (1)、当F为BE的中点时,求证:AM=CE;(2)、若=2,求的值;(3)、若MN∥BE,求的值.
(1)、当F为BE的中点时,求证:AM=CE;(2)、若=2,求的值;(3)、若MN∥BE,求的值.