（浙教版）2022-2023学年九年级数学下册第一章 解直角三角形 单元测试
试卷更新日期：2022-10-24 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 在下列实数中，无理数是（ ）A、sin45° B、 C、0.3 D、tan45°2. 在下列网格中，小正方形的边长为1，点A，B，求∠A的余弦值（ ）
A、 B、 C、 D、3. 如图，A，B，C是3×1的正方形网格中的三个格点，则 tan∠ABC的值为（ ）
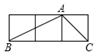A、 B、 C、 D、4. 四位学生用计算器求cos 27°40'的近似值的结果如下，正确的是（ ）
A、0.885 7 B、0.885 6 C、0.885 2 D、0.885 15. sin58°、cos58°、cos28°的大小关系是（ ）A、cos28°＜cos58°＜sin58° B、sin58°＜cos28°＜cos58° C、cos58°＜sin58°＜cos28° D、sin58°＜cos58°＜cos28°6. 在△ABC中，AB=3，AC= ．当∠B最大时，BC的长是（ ）A、 B、 C、 D、27.利用计算器求tan45°时，依次按键
则计算器上显示的结果是（ ）A． B． C．
A、0.5 B、0.707 C、0.866 D、18. 如图，AC是旗杆AB的一根拉线，拉直AC时，测得BC＝3米，∠ACB＝50°，则AB的高为（ ）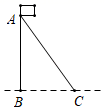
A、3cos50°米 B、3tan50°米 C、 米 D、 米9. 如图，在坡度为 的山坡上种树，要求相邻两棵树的水平距离是6m，则斜坡上相邻两棵树的坡面距离是（ ）
A、3m B、3 m C、12m D、6m10. 如图，在平地上种植树木时，要求株距（相邻两树间的水平距离）都为4m．如果在坡度为0.75的山坡上种树，也要求株距为4m，那么相邻两树间的坡面距离为（ ）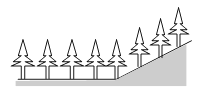
A、5m B、6m C、7m D、8m二、填空题（每题3分，共15分）
-
11. 如图，在⊙O中，弦AB的长为 ， 圆心到弦AB的距离为1，则∠BOC的度数为.
12. 在Rt△ABC中，∠C＝90°，若AB＝4，sinA＝
，则斜边上的高等于 ． 13. 如果cosA=0.8888，则∠A≈ ．（精确到″）14. 如图，矩形ABCD沿对角线BD翻折后，点C落在点E处．连结CE交边AD于点F ． 如果DF＝1，BC＝4，那么AE的长等于 ．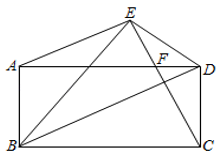
15. 如图，Rt△ABC中，∠C＝90o ， ∠A＝30o ， BC＝1，以点B为圆心，以BC长度为半径作弧，交BA于点D，以点C为圆心，以大于 为半径作弧，接着再以点D为圆心，以相同长度为半径作弧，两弧交于点E，作射线BE交CA于点F，以点B为圆心，以BF为长度作弧，交BA于点G，则阴影部分的面积为.
三、解答题（共8题，共55分）
-
16. 如图1，一扇窗户打开一定角度，其中一端固定在窗户边OM上的点A处，另一端B在边ON上滑动，图2为某一位置从上往下看的平面图，测得∠ABO为37°，∠AOB为45°，OB长为35厘米，求AB的长（参考数据：sin37°≈0.6，cos37°≈0.8，tan37°≈0.75）
17. 为提高城市幸福感，某市旅游局开发了风景优美的景点C ， 已知景点C在景点A北偏东37°方向上，景点C在景点B北偏东60°方向上，且景点B在景点A正北方向，A ， B两个景点相距980米，求 和 的长（结果取整数）.参考数据： ， ， ， 取1.73.
18. 如图所示，建筑物 座落在一斜坡的坡顶的平地上，当太阳光线与水平线夹角成60°时，测得建筑物 在坡顶平地上的一部分影子 米，在斜坡 上的另一部分影子 米，且斜坡 的坡度为 （即 ） 求建筑物 的高度.（结果保留根号）
19. 如图，一艘船由A港沿北偏东65°方向航行 海里至B港，然后再沿北偏西40°方向航行至C港，C港在A港北偏东20°方向，求A ， C两港之间的距离为多少海里.（保留根号）
20. 第十一届全国少数民族传统体育运动会于2019年9月8日至16日在郑州举行，据了解，该赛事每四年举办一届，是我国规格最高、规模最大的综合性民族体育盛会，其中，花炮、押加、民族式摔跤三个项目的比赛在郑州大学主校区进行.如图，钟楼是郑州大学主校区标志性建筑物之一，是郑大的“第一高度”，寓意来自五湖四海的郑大人的团结和凝聚.小刚站在钟楼前C处测得钟楼顶A的仰角为53°，小强站在对面的教学楼三楼上的D处测得钟楼顶A的仰角为45°，此时，两人的水平距离EC为4m，已知教学楼三楼所在的高度为10m，根据测得的数据，计算钟楼AB的高度.（参考数据：sin53°≈ ，cos53°≈ ，tan53°≈ ）
21. 某校门口竖着“前方学校，减速慢行”的交通指示牌CD ， 数学“综合与实践”小组的同学将“测量交通指示牌CD的高度”作为一项课题活动，他们定好了如下测量方案：项目
内容
课题
测量交通指示牌CD的高度
测量示意图
测量步骤
(1)从交通指示牌下的点M处出发向前走10 米到达A处；
(2)在点A处用量角仪测得∠DAM＝27°；
(3)从点A沿直线MA向前走10米到达B处；(4)在点B处用量角仪测得∠CBA＝18°．
请你帮助该小组同学根据上表中的测量数据，求出交通指示牌CD的高度．(参考数据sin27°≈0.45，cos27°≈0.89，tan27°≈0.51，sin18°≈0.31，cos18°≈0.95，tan18°≈0.32)
22. 某校创客社团计划利用新购买的无人机设备测量学校旗杆 的高.他们先将无人机放在旗杆前的点C处（无人机自身的高度忽略不计），测得此时点A的仰角为 ，因为旗杆底部有台阶，所以不能直接测出垂足B到点C的距离.无人机起飞后，被风吹至点D处，此时无人机距地面的高度为3米，测得此时点C的俯角为 ，点A的仰角为 ，且点B，C，D在同一平面内，求旗杆 的高度.（计算结果精确到0.1米，参考数据： ， ， ， ， ）
23. 光明中学九年级（1）班开展数学实践活动，小李沿着东西方向的公路以50 m/min的速度向正东方向行走，在A处测得建筑物C在北偏东60°方向上，20min后他走到B处，测得建筑物C在北偏西45°方向上，求建筑物C到公路AB的距离．（已知 ）