(浙教版)2022-2023学年九年级数学下册1.2锐角三角函数的计算 同步测试
试卷更新日期:2022-10-24 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图,已知:45°<∠A<90°,则下列各式成立的是( )
 A、sinA=cosA B、sinA>cosA C、sinA>tanA D、sinA<cosA2. 已知β为锐角,cos β≤ ,则β的取值范围为( )
A、sinA=cosA B、sinA>cosA C、sinA>tanA D、sinA<cosA2. 已知β为锐角,cos β≤ ,则β的取值范围为( )
A、30°≤β<90° B、0°<β≤60° C、60°≤β<90° D、30°≤β<60°3. 用计算器比较tan 25°,sin 27°,cos 26°的大小关系是( )A、tan 25°<cos 26°<sin 27° B、tan 25°<sin 27°<cos 26° C、sin 27°<tan 25°<cos 26° D、cos 26°<tan 25°<sin 27°4. 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )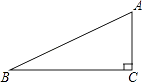 A、
A、 B、
B、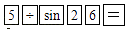 C、
C、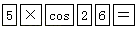 D、
D、 5. 如图,△ABC是锐角三角形,sinC= ,则sinA的取值范围是( )
5. 如图,△ABC是锐角三角形,sinC= ,则sinA的取值范围是( ) A、0 B、 C、 D、6. 若锐角α满足sinα> ,且cosα> ,则α的范围是( )A、0°<α<30° B、30°<α<60° C、60°<α<90° D、45°<α<90°7. 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( )
A、0 B、 C、 D、6. 若锐角α满足sinα> ,且cosα> ,则α的范围是( )A、0°<α<30° B、30°<α<60° C、60°<α<90° D、45°<α<90°7. 如图,在△ABC中,∠ACB=90°,∠ABC=26°,BC=5.若用科学计算器求边AC的长,则下列按键顺序正确的是( ) A、5÷tan26°= B、5÷sin26°= C、5×cos26°= D、5×tan26°=8. 如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )
A、5÷tan26°= B、5÷sin26°= C、5×cos26°= D、5×tan26°=8. 如图,梯子跟地面的夹角为∠A,关于∠A的三角函数值与梯子的倾斜程度之间,叙述正确的是( )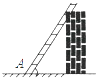 A、sinA的值越小,梯子越陡 B、cosA的值越小,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的函数值无关9. 把Rt△ABC各边的长度都扩大3倍得Rt△A′B′C′,那么锐角A、A′的余弦值的关系为( )
A、sinA的值越小,梯子越陡 B、cosA的值越小,梯子越陡 C、tanA的值越小,梯子越陡 D、陡缓程度与∠A的函数值无关9. 把Rt△ABC各边的长度都扩大3倍得Rt△A′B′C′,那么锐角A、A′的余弦值的关系为( )
A、cosA=cosA′ B、cosA=3cosA′ C、3cosA=cosA′ D、不能确定10. 如图,抛物线y=-x2+k与x轴交于A(-3,0)和B(3,0),有一动点C在线段AB上从点A运动到点B(不与A,B重合),分别以AC,BC为底边作等腰△ADC和等腰△BEC,点D,E恰好落在此抛物线上,在整个运动过程中, ∠DCE的变化情况是( )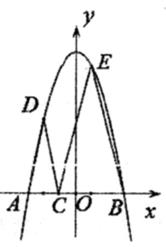 A、保持不变 B、一直减小 C、先增大后减小 D、先减小后增大
A、保持不变 B、一直减小 C、先增大后减小 D、先减小后增大二、解答题(共8题,共55分)
-
11. 计算(结果保留小数点后四位)
(1)sin23°5′+cos66°45′
(2)sin27.8°﹣tan15°8′.
12. 已知sin A=0.328 6,tan B=10.08,利用计算器求锐角A,B.(结果精确到0.01°)13. 已知,凸4n+2边形A1A2…A4n+2(n是非零自然数)各内角都是30°的整数倍,又关于x的方程:均有实根,求这凸4n+2边形各内角的度数.
14. 设a、b、c是直角三角形的三边,c为斜边,n为正整数,试判断an+bn与cn的关系,并证明你的结论.15. 已知:如图,在△ABC中,AB=8,AC=9,∠A=48°.求:AB边上的高(精确到0.01);
 16. 等腰三角形中,两腰和底的长分别是10和13,求三角形的三个内角的度数(精确到l′).17. (1)用计算器计算并验证sin25°+sin46°与sin71°之间的大小关系:
16. 等腰三角形中,两腰和底的长分别是10和13,求三角形的三个内角的度数(精确到l′).17. (1)用计算器计算并验证sin25°+sin46°与sin71°之间的大小关系:(2)若α、β、α+β都是锐角,猜想sinα+sinβ与sin(α+β)的大小关系:
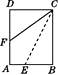
(3)请借助如图的图形证明上述猜想.
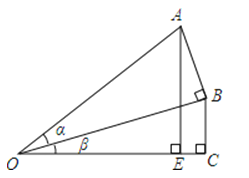 18. 我们知道:sin30°= , tan30°= , sin45°= , tan45°=1,sin60°= , tan60°= , 由此我们可以看到tan30°>sin30°,tan45°>sin45°,tan60°>sin60°,那么对于任意锐角α,是否可以得到tanα>sinα呢?请结合锐角三角函数的定义加以说明.
18. 我们知道:sin30°= , tan30°= , sin45°= , tan45°=1,sin60°= , tan60°= , 由此我们可以看到tan30°>sin30°,tan45°>sin45°,tan60°>sin60°,那么对于任意锐角α,是否可以得到tanα>sinα呢?请结合锐角三角函数的定义加以说明.
三、填空题(每题3分,共15分)
-
19. 比较大小:sin35°cos45°.20. 已知 ,且 为锐角,则m的取值范围是 .