2022年秋季北师版数学九年级上学期期中复习检测A
试卷更新日期:2022-10-24 类型:期中考试
一、单选题(每题3分,共30分)
-
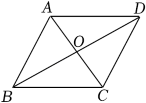
1. 如图,▱ABCD的对角线AC和BD相交于点O,下列说法正确的是( )
 A、若OB=OD,则▱ABCD是菱形 B、若AC=BD,则▱ABCD是菱形 C、若OA=OD,则▱ABCD是菱形 D、若AC⊥BD,则▱ABCD是菱形2. 若x=﹣1是方程x2+x+m=0的一个根,则此方程的另一个根是( )A、﹣1 B、0 C、1 D、23. 某校开展岗位体验劳动教育活动,设置了“安全小卫士”“环卫小卫士”“图书管理小卫士”“宿舍管理小卫士”共四个岗位,每个岗位体验人数不限且每位同学只能从中随机选择一个岗位进行体验、甲、乙两名同学都参加了此项活动,则这两名同学恰好在同一岗位体验的概率为( )A、 B、 C、 D、4. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( )
A、若OB=OD,则▱ABCD是菱形 B、若AC=BD,则▱ABCD是菱形 C、若OA=OD,则▱ABCD是菱形 D、若AC⊥BD,则▱ABCD是菱形2. 若x=﹣1是方程x2+x+m=0的一个根,则此方程的另一个根是( )A、﹣1 B、0 C、1 D、23. 某校开展岗位体验劳动教育活动,设置了“安全小卫士”“环卫小卫士”“图书管理小卫士”“宿舍管理小卫士”共四个岗位,每个岗位体验人数不限且每位同学只能从中随机选择一个岗位进行体验、甲、乙两名同学都参加了此项活动,则这两名同学恰好在同一岗位体验的概率为( )A、 B、 C、 D、4. 如图,正方形的对角线交于点O,点E是直线上一动点.若 , 则的最小值是( ) A、 B、 C、 D、5. 用配方法解一元二次方程时,将它化为的形式,则a+b的值为( )A、 B、 C、2 D、6. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )
A、 B、 C、 D、5. 用配方法解一元二次方程时,将它化为的形式,则a+b的值为( )A、 B、 C、2 D、6. 如图,菱形ABCD的对角线AC、BD相交于点O,过点D作DH⊥AB于点H,连接OH,OH=4,若菱形ABCD的面积为32 , 则CD的长为( )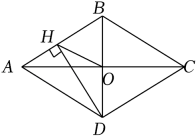 A、4 B、4 C、8 D、87. 已知 , 是方程的两个实数根,则代数式的值是( )A、4045 B、4044 C、2022 D、18. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )
A、4 B、4 C、8 D、87. 已知 , 是方程的两个实数根,则代数式的值是( )A、4045 B、4044 C、2022 D、18. 如图,在平面直角坐标系中,为的边上一点, , 过作交于点 , 、两点纵坐标分别为1、3,则点的纵坐标为( )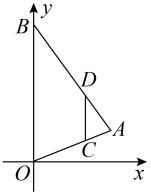 A、4 B、5 C、6 D、79. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛,单循环比赛共进行了45场,共有多少支队伍参加比赛?( )A、8 B、10 C、7 D、910. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( )
A、4 B、5 C、6 D、79. 2022年北京冬奥会女子冰壶比赛有若干支队伍参加了单循环比赛,单循环比赛共进行了45场,共有多少支队伍参加比赛?( )A、8 B、10 C、7 D、910. 如图,点D为边上任一点,交于点E,连接相交于点F,则下列等式中不成立的是( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题(每题3分,共18分)
-
11. 数学兴趣小组通过测量旗杆的影长来求旗杆的高度,他们在某一时刻测得高为2米的标杆影长为1.2米,此时旗杆影长为7.2米,则旗杆的高度为米.
 12. 若实数a、b分别满足a2﹣4a+3=0,b2﹣4b+3=0,且a≠b,则的值为 .13. 如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .
12. 若实数a、b分别满足a2﹣4a+3=0,b2﹣4b+3=0,且a≠b,则的值为 .13. 如图,将矩形纸片ABCD沿CE折叠,使点B落在边AD上的点F处.若点E在边AB上,AB=3,BC=5,则AE= .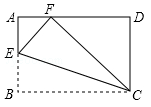 14. 如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE、BC于点H、G,则BG=.
14. 如图,正方形ABCD的边长为8,点E是CD的中点,HG垂直平分AE且分别交AE、BC于点H、G,则BG=. 15. 如图,小明同学用一张长11cm,宽7cm的矩形纸板制作一个底面积为的无盖长方体纸盒,他将纸板的四个角各剪去一个同样大小的正方形,将四周向上折叠即可(损耗不计).设剪去的正方形边长为xcm,则可列出关于x的方程为 .
15. 如图,小明同学用一张长11cm,宽7cm的矩形纸板制作一个底面积为的无盖长方体纸盒,他将纸板的四个角各剪去一个同样大小的正方形,将四周向上折叠即可(损耗不计).设剪去的正方形边长为xcm,则可列出关于x的方程为 . 16. 如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF= , 则BD的长为(结果保留很号).
16. 如图,四边形ABCD为菱形,∠ABC=80°,延长BC到E,在∠DCE内作射钱CM,使得∠ECM=30°,过点D作DF⊥CM,垂足为F.若DF= , 则BD的长为(结果保留很号).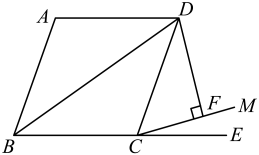
三、解答题(共8题,共72分)
-
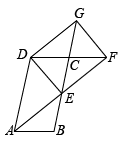
17. 解方程(1)、(2)、(配方法)18. 如图,▱ABCD中,E为BC边的中点,连接AE并延长交DC的延长线于点F,延长EC至点G,使CG=CE,连接DG、DE、FG.
 (1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.19. 在习近平总书记视察广西、亲临柳州视察指导一周年之际,某校开展“紧跟伟大复兴领航人踔厉笃行”主题演讲比赛,演讲的题目有: 《同甘共苦民族情》《民族团结一家亲,一起向未来》《画出最美同心圆》。 赛前采用抽签的方式确定各班演讲题目,将演讲题目制成编号为 , , 的 张卡片 ( 如图所示,卡片除编号和内容外,其余完全相同)。 现将这 张卡片背面朝上,洗匀放好.
(1)、求证:△ABE≌△FCE;(2)、若AD=2AB,求证:四边形DEFG是矩形.19. 在习近平总书记视察广西、亲临柳州视察指导一周年之际,某校开展“紧跟伟大复兴领航人踔厉笃行”主题演讲比赛,演讲的题目有: 《同甘共苦民族情》《民族团结一家亲,一起向未来》《画出最美同心圆》。 赛前采用抽签的方式确定各班演讲题目,将演讲题目制成编号为 , , 的 张卡片 ( 如图所示,卡片除编号和内容外,其余完全相同)。 现将这 张卡片背面朝上,洗匀放好. (1)、某班从 张卡片中随机抽取 张,抽到卡片 的概率为;(2)、若七 班从 张卡片中随机抽取 张,记下题目后放回洗匀,再由七 班从中随机抽取 张,请用列表或画树状图的方法,求这两个班抽到不同卡片的概率. ( 这 张卡片分别用它们的编号 , , 表示 )20. 如图,在矩形ABCD中,AB=BC,点F在BC边的延长线上,点P是线段BC上一点(与点B,C不重合),连接AP并延长,过点C作CG⊥AP,垂足为E.
(1)、某班从 张卡片中随机抽取 张,抽到卡片 的概率为;(2)、若七 班从 张卡片中随机抽取 张,记下题目后放回洗匀,再由七 班从中随机抽取 张,请用列表或画树状图的方法,求这两个班抽到不同卡片的概率. ( 这 张卡片分别用它们的编号 , , 表示 )20. 如图,在矩形ABCD中,AB=BC,点F在BC边的延长线上,点P是线段BC上一点(与点B,C不重合),连接AP并延长,过点C作CG⊥AP,垂足为E. (1)、若CG为∠DCF的平分线.请判断BP与CP的数量关系,并证明;(2)、若AB=3,△ABP≌△CEP,求BP的长.21. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.
(1)、若CG为∠DCF的平分线.请判断BP与CP的数量关系,并证明;(2)、若AB=3,△ABP≌△CEP,求BP的长.21. 如图①、图②、图③均是的正方形网格,每个小正方形的边长均为1,其顶点称为格点,的顶点均在格点上.只用无刻度的直尺,在给定的网格中,按下列要求作图,保留作图痕迹.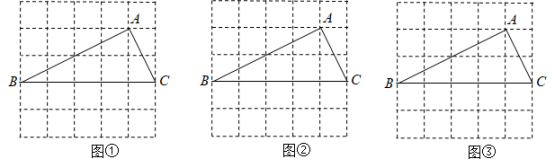 (1)、网格中的形状是;(2)、在图①中确定一点D,连结、 , 使与全等:(3)、在图②中的边上确定一点E,连结 , 使:(4)、在图③中的边上确定一点P,在边BC上确定一点Q,连结 , 使 , 且相似比为1:2.22. 2022北京冬奥会期间,某网店直接从工厂购进A、B两款冰嫩墩钥匙扣,进货价和销售价如下表:(注:利润=销售价-进货价)
(1)、网格中的形状是;(2)、在图①中确定一点D,连结、 , 使与全等:(3)、在图②中的边上确定一点E,连结 , 使:(4)、在图③中的边上确定一点P,在边BC上确定一点Q,连结 , 使 , 且相似比为1:2.22. 2022北京冬奥会期间,某网店直接从工厂购进A、B两款冰嫩墩钥匙扣,进货价和销售价如下表:(注:利润=销售价-进货价)类别
价格
A款钥匙扣
B款钥匙扣
进货价(元/件)
30
25
销售价(元/件)
45
37
(1)、网店第一次用850元购进A、B两款钥匙扣共30件,求两款钥匙扣分别购进的件数;(2)、第一次购进的冰墩嫩钥匙扣售完后,该网店计划再次购进A、B两款冰墩墩钥匙扣共80件(进货价和销售价都不变),且进货总价不高于2200元.应如何设计进货方案,才能获得最大销售利润,最大销售利润是多少?(3)、冬奥会临近结束时,网店打算把B款钥匙扣调价销售.如果按照原价销售,平均每天可售4件.经调查发现,每降价1元,平均每天可多售2件,将销售价定为每件多少元时,才能使B款钥匙扣平均每天销售利润为90元?23. 阅读材料:材料1:若关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根为x1 , x2 , 则x1+x2= ,x1x2=
材料2:已知一元二次方程x2-x-1=0的两个实数根分别为m,n,求m2n+mn2的值.
解:∵一元二次方程x2-x-1=0的两个实数根分别为m,n,
∴m+n=1,mn=-1,
则m2n+mn2=mn(m+n)=-1×1=-1
根据上述材料,结合你所学的知识,完成下列问题:
(1)、材料理解:一元二次方程2x2-3x-1=0的两个根为x1 , x2 , 则x1+x2=;x1x2= .(2)、类比应用:已知一元二次方程2x2-3x-1=0的两根分别为m、n,求 的值.(3)、思维拓展:已知实数s、t满足2s2-3s-1=0,2t2-3t-1=0,且s≠t,求 的值.24. 已知点在正方形的对角线上,正方形与正方形有公共点 .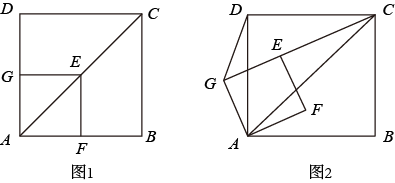 (1)、如图1,当点在上,在上,求的值为多少;(2)、将正方形绕点逆时针方向旋转 , 如图2,求:的值为多少;(3)、 , , 将正方形绕逆时针方向旋转 , 当 , , 三点共线时,请直接写出的长度.
(1)、如图1,当点在上,在上,求的值为多少;(2)、将正方形绕点逆时针方向旋转 , 如图2,求:的值为多少;(3)、 , , 将正方形绕逆时针方向旋转 , 当 , , 三点共线时,请直接写出的长度.