（浙教版）2022-2023学年九年级数学下册1.1锐角三角函数同步测试

试卷更新日期：2022-10-24 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 如图，点A，B，C在正方形网格的格点上，则sin∠ABC＝（　　）

A、 $\frac{\sqrt{2}}{6}$ B、 $\frac{\sqrt{26}}{26}$ C、 $\frac{\sqrt{26}}{13}$ D、 $\frac{\sqrt{13}}{13}$

查看试题解析
2. 如图，已知AB是⊙O的直径，弦CD⊥AB，垂足为E，且∠BCD＝30°，CD＝4 $\sqrt{3}$ ．则图中阴影部分的面积S_阴影＝（）

A、2π B、 $\frac{8}{3}$ π C、 $\frac{4}{3}$ π D、 $\frac{3}{8}$ π

查看试题解析
3. 在△ABC中，∠A和∠C都是锐角，且sinA= $\frac{\sqrt{3}}{2}$ ，tanC= $\sqrt{3}$ ，则∠ABC是（）

A、直角三角形 B、钝角三角形 C、等边三角形 D、不能确定

查看试题解析
4. 如图，⊙O是△ABC的外接圆，直径BD长为4，sin∠BAC＝ $\frac{3}{4}$ ，则BC的长为（）

A、 $\frac{5}{2}$ B、3 C、 $\sqrt{7}$ D、 $\sqrt{11}$

查看试题解析
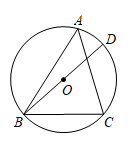5. 如图，在菱形ABCD中，∠ABC＝120°，AB＝10cm，点 P是这个菱形内部或边上的一点.若以P，B，C为顶点的三角形是等腰三角形，则P，A（P，A两点不重合）两点间的最短距离为（）

A、10 B、5 $\sqrt{3}$ C、10 $\sqrt{3}$ －10 D、10－5 $\sqrt{3}$

查看试题解析
6. 如图所示，△ABC的顶点是正方形网格的格点，则sin∠A的值为（）

A、 $\frac{1}{2}$ B、 $\frac{\sqrt{10}}{10}$ C、 $\frac{\sqrt{5}}{5}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
7. 如图，矩形ABCD中，AD＝4，AB＝5，E是AB边上的一点，连接DE、EC.若EC平分∠BED，则sin∠BCE的值是（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{2 \sqrt{5}}{5}$ C、 $\frac{\sqrt{3}}{2}$ D、 $\frac{2}{3}$

查看试题解析
8. 如图，D为平面直角坐标系内一点，OD与x轴构成∠1，那么tan∠1=（）

A、 $\frac{3}{2}$ B、 $\frac{2}{\sqrt{13}}$ C、 $\frac{2}{3}$ D、 $\frac{3}{\sqrt{13}}$

查看试题解析
9. 如图，在⊙O中，弦AB的长是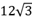 cm，弦AB的弦心距为6cm，E是⊙O优弧AEB上一点.则∠AEB的度数为（）

A、60° B、45° C、30° D、80°

查看试题解析
10. 在 $R t △ A B C$ 中， $∠ C = 90 °$ ， $t a n A = \frac{4}{3}$ ，则 $s i n B$ 的值为（）

A、 $\frac{3}{5}$ B、 $\frac{4}{5}$ C、 $\frac{4}{3}$ D、 $\frac{3}{4}$

查看试题解析

二、填空题（每题3分，共15分）

11. 如图，在△ABC中，∠C = 90°，点D在边BC上，以OA为半径的 $⊙ O$ 经过点D，连接AD，且AD平分∠BAC，若∠BAC = 60°， $⊙ O$ 的半径为2，则阴影部分的面积为 .

查看试题解析
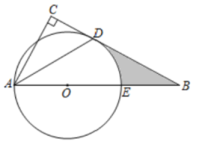12. △ABC内接于圆 $O$ ，且 $AB = AC$ ，圆 $O$ 的直径为 $10 cm$ ， $BC = 6 cm$ ，则 $sinB =$ .

查看试题解析
13. 如图，在半径为6的⊙O中，点A是劣弧 $\overset{⌢}{B C}$ 的中点，点D是优弧 $\overset{⌢}{B C}$ 上一点， $∠ t a n D = \frac{\sqrt{3}}{3}$ ，则BC的长为.

查看试题解析
14. 如图，在5×5的正方形网格中，点A，B，C，D为格点，AB交CD于点O，则tan∠AOC＝.

查看试题解析
15. 如图，正方形ABCD中，点E，F分别为CD，DA延长线上的点，连接EF，BF，BE，BE交AD于点P，过点F作FK⊥BE垂足为G，FK与AB，CD分别交于点H，K，若DC=DE，∠EFB=∠FBC.则下列结论中：①BP＝HK；②∠ABF+∠FEB＝45°；③PG：GB：PE＝1：2：3；④ $\sin ∠ A B F = \frac{\sqrt{10}}{10}$ ；⑤若连接AG，则 $A H + A P = \sqrt{2} A G$ ；⑥HF²+HK²＝2HB².结论正确的有（只填序号）.

查看试题解析

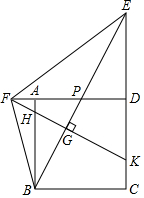
三、解答题（共8题，共55分）

16. 先化简，再求代数式 $\frac{x + 1}{x} \div (x - \frac{x^{2} + 1}{2 x})$ 的值，其中 $x = 2 s i n 30 ° + t a n 60 °$ ．

查看试题解析
17. 已知：在Rt△ABC 中，∠C=90°，sinA= $\frac{2}{3}$ ， AC=10，求△ABC的面积。

查看试题解析
18. 如图所示，∠C＝90°，BC＝8cm，cosA＝3︰5，点P从点B出发，沿BC向点C以2cm/s的速度移动，点Q从点C出发沿CA向点A以1cm/s的速度移动，如果P、Q分别从B、C同时出发，过多少秒时，以C、P、Q为顶点的三角形恰与△ABC相似？

查看试题解析
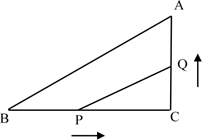19. 如图，秋千拉绳长AB为3米，静止时踩板离地面0.5米，某小朋友荡该秋千时，秋千在最高处时踩板离地面2米（左右对称），请计算该秋千所荡过的圆弧长（精确到0.1米）？

查看试题解析
20. 如图，在△ABC中，AB＝AC，⊙O是△ABC的外接圆，AE⊥AB交BC于点D，交⊙O于点E，F在DA的延长线上，且AF＝AD．若AF＝3，tan∠ABD＝ $\frac{3}{4}$ ，求⊙O的直径．

查看试题解析
21. 如图，网格中的每个小正方形的边长都是1，△ABC每个顶点都在网格的交点处，求sin∠CAB的值.

查看试题解析
22. （1）计算： ${(\sqrt{3} - 2)}^{0} - \sqrt{27} + 3 \tan 60 °$ ；
（2）先化简再求值：求（2x+y）（2x﹣y）﹣（2x+y）²+2y²的值，其中 $x = \frac{3}{2} y = - \frac{1}{3}$ ．

查看试题解析
23.
如图，将含30°角的直角三角板ABC（∠A=30°）绕其直角顶点C顺时针旋转α角（0°＜α＜90°），得到Rt△A′B′C，A′C与AB交于点D，过点D作DE∥A′B′交CB′于点E，连接BE．易知，在旋转过程中，△BDE为直角三角形．设BC=1，AD=x，△BDE的面积为S．
（1）当α=30°时，求x的值．
（2）求S与x的函数关系式，并写出x的取值范围；

查看试题解析

（浙教版）2022-2023学年九年级数学下册1.1锐角三角函数 同步测试

一、单选题（每题3分，共30分）

二、填空题（每题3分，共15分）

三、解答题（共8题，共55分）

（浙教版）2022-2023学年九年级数学下册1.1锐角三角函数同步测试