(北师大版)2022-2023学年九年级数学下册2.4二次函数的应用 同步测试
试卷更新日期:2022-10-24 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 某旅行社组团去外地旅游,30人起组团,每人单价800元.旅行社对超过30人的团给予优惠,即旅游团的人数每增加一人,每人的单价就降低10元,若这个旅行社要获得最大营业额,则这个旅游团的人数是( )A、55 B、56 C、57 D、582. 在特定条件下,篮球赛中进攻球员投球后,篮球的运行轨迹是开口向下的抛物线的一部分.“盖帽”是一种常见的防守手段,防守队员在篮球上升阶段将球拦截即为“盖帽”,而防守队员在篮球下降阶段将球拦截则属“违规”.对于某次投篮而言,如果忽略其他因素的影响,篮球处于上升阶段的水平距离越长,则被“盖帽”的可能性越大.收集几次篮球比赛的数据之后,某球员投篮可以简化为下述数学模型:如图所示,该球员的投篮出手点为P,篮框中心点为Q,他可以选择让篮球在运行途中经过A,B,C,D四个点中的某一点并命中Q,忽略其他因素的影响,那么被“盖帽”P的可能性最大的线路是( )
 A、 B、 C、 D、3. 用绳子围成周长为10(m)的矩形,记矩形的一边长为x(m),面积为S(m2).当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( )A、一次函数关系 B、二次函数关系 C、反比例函数关系 D、正比例函数关系4. 如图所示,将一根长 m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( )
A、 B、 C、 D、3. 用绳子围成周长为10(m)的矩形,记矩形的一边长为x(m),面积为S(m2).当x在一定范围内变化时,S随x的变化而变化,则S与x满足的函数关系是( )A、一次函数关系 B、二次函数关系 C、反比例函数关系 D、正比例函数关系4. 如图所示,将一根长 m的铁丝首尾相接围成矩形,则矩形的面积与其一边满足的函数关系是( ) A、正比例函数关系 B、一次函数关系 C、二次函数关系 D、反比例函数关系5. 如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )
A、正比例函数关系 B、一次函数关系 C、二次函数关系 D、反比例函数关系5. 如图,排球运动员站在点O处练习发球,将球从O点正上方2m的A处发出,把球看成点,其运行的高度y(m)与运行的水平距离x(m)满足关系式y=a(x﹣k)2+h.已知球与D点的水平距离为6m时,达到最高2.6m,球网与D点的水平距离为9m.高度为2.43m,球场的边界距O点的水平距离为18m,则下列判断正确的是( )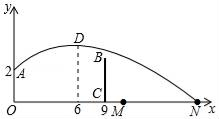 A、球不会过网 B、球会过球网但不会出界 C、球会过球网并会出界 D、无法确定6. 如图,已知AB=8,P为线段AB上的一个动点,以AP为边作正三角形APC,延长PC到点E使PE=PB,D,F分别是AC,BE的中点.当点P在线段AB上移动时,点D,F之间的距离的最小值为( )
A、球不会过网 B、球会过球网但不会出界 C、球会过球网并会出界 D、无法确定6. 如图,已知AB=8,P为线段AB上的一个动点,以AP为边作正三角形APC,延长PC到点E使PE=PB,D,F分别是AC,BE的中点.当点P在线段AB上移动时,点D,F之间的距离的最小值为( ) A、2 B、4 C、
A、2 B、4 C、 D、
D、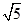 7. 如图,在平面直角坐标系响,抛物线y=a(x-m)2+1(a<0)与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C,顶点是D,且∠DAB=45°,点C绕O逆时针旋转90°得到点C',当 ≤m≤ 之时,BC'的长度范围是( )
7. 如图,在平面直角坐标系响,抛物线y=a(x-m)2+1(a<0)与x轴交于点A和点B(点A在点B的左侧),与y轴交于点C,顶点是D,且∠DAB=45°,点C绕O逆时针旋转90°得到点C',当 ≤m≤ 之时,BC'的长度范围是( ) A、0≤BC'≤
A、0≤BC'≤ B、
B、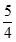 ≤BC'≤
≤BC'≤  C、
C、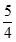 ≤BC'≤
≤BC'≤  D、0≤BC'≤
D、0≤BC'≤ 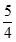 8. 如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( )
8. 如图所示是一个抛物线形桥拱的示意图,在所给出的平面直角坐标系中,当水位在AB位置时,水面宽度为10m,此时水面到桥拱的距离是4m,则抛物线的函数关系式为( ) A、y=
A、y=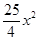 B、y=﹣
B、y=﹣ 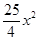 C、y=﹣
C、y=﹣ 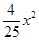 D、y=
D、y= 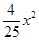 9. 如图,有一座抛物线拱桥,当水位在AB位置时,桥拱顶离水面2m,水面宽4m.若水面下降1m,则水面宽CD为( )
9. 如图,有一座抛物线拱桥,当水位在AB位置时,桥拱顶离水面2m,水面宽4m.若水面下降1m,则水面宽CD为( ) A、5m B、6m C、 m D、2 m10. 某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(单位:万元)与销售量x(单位:辆)之间分别满足:y1=﹣x2+10x,y2=2x,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为( )A、30万元 B、40万元 C、45万元 D、46万元
A、5m B、6m C、 m D、2 m10. 某公司在甲、乙两地同时销售某种品牌的汽车.已知在甲、乙两地的销售利润y(单位:万元)与销售量x(单位:辆)之间分别满足:y1=﹣x2+10x,y2=2x,若该公司在甲,乙两地共销售15辆该品牌的汽车,则能获得的最大利润为( )A、30万元 B、40万元 C、45万元 D、46万元二、填空题(每题3分,共15分)
-
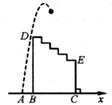
11. 校运动会铅球比赛时,小林推出的铅球行进的高度y(米)与水平距离x(米)满足关系式 , 则小林这次铅球推出的距离是米.12. 如图是王明正在设计的一动画示意图,×轴上依次有A,B,C三个点,且AB=2,在BC上方有五个台阶(各拐角均为90°),每个台阶的高、宽分别是1和1.5,第一个台阶到x轴距离BD=10.从点A处向右,上方沿抛物线y=-x2+4x+12发出一个带光的点P.当点P落在台阶上时,落点的坐标是 .
 13. 图1是苍南县中心湖公园里的一座彩虹桥两条抛物线型钢梁在桥面上的跨度分别为米和米(如图2所示),x轴表示桥面,米.若两抛物线交y轴于同一点,且它们的形状相同,则的值为.
13. 图1是苍南县中心湖公园里的一座彩虹桥两条抛物线型钢梁在桥面上的跨度分别为米和米(如图2所示),x轴表示桥面,米.若两抛物线交y轴于同一点,且它们的形状相同,则的值为. 14. 如图,某农场拟建一矩形饲养室,饲养室的一面靠墙(墙足够长),并在图中所示位置开2m的门,已知建筑围栏的材料可建围墙共66m,设饲养室的长为x(m),占地面积为y(m2),请列出y关于x的函数关系式:.(不用写x的取值范围)
14. 如图,某农场拟建一矩形饲养室,饲养室的一面靠墙(墙足够长),并在图中所示位置开2m的门,已知建筑围栏的材料可建围墙共66m,设饲养室的长为x(m),占地面积为y(m2),请列出y关于x的函数关系式:.(不用写x的取值范围)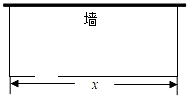 15. 教练对小明推铅球的录像进行技术分析,发现铅球行进高度 与水平距离 之间的关系为 ,由此可知铅球推出的距离是m.
15. 教练对小明推铅球的录像进行技术分析,发现铅球行进高度 与水平距离 之间的关系为 ,由此可知铅球推出的距离是m.三、解答题(共8题,共55分)
-
16. 某家电生产厂家去年销往农村的某品牌洗碗机每台的售价y(元)与月份x之间满足函数关系,去年的月销售量P(万台)与月份x之间成一次函数关系y=-50x+2600,其中两个月的销售情况如下表:
月份x
1月
5月
销量P
3.9万台
4.3万台
求该品牌洗碗机在去年哪个月销往农村的销售金额最大?最大是多少?
17. 如图所示,已知边长为4的正方形钢板有一个角锈蚀,其中AF=2,BF=1。为了合理利用这块钢板.将在五边形EABCD内截取一个矩形块MDNP,使点P在AB上,且要求面积最大,求钢板的最大利用率。 18. 如图,一块草地是长80 m,宽60 m的矩形,欲在中间修筑两条互相垂直的宽为xm的小路,这时草坪面积为y m2 . 求y与x的函数关系式,并写出自变量x的取值.
18. 如图,一块草地是长80 m,宽60 m的矩形,欲在中间修筑两条互相垂直的宽为xm的小路,这时草坪面积为y m2 . 求y与x的函数关系式,并写出自变量x的取值. 19. 为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一条矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带BC边长为xm,绿化带的面积为ym2 , 求y与x之间的函数关系式,并写出自变量x的取值范围.
19. 为了改善小区环境,某小区决定要在一块一边靠墙(墙长25m)的空地上修建一条矩形绿化带ABCD,绿化带一边靠墙,另三边用总长为40m的栅栏围住(如图).若设绿化带BC边长为xm,绿化带的面积为ym2 , 求y与x之间的函数关系式,并写出自变量x的取值范围. 20. 某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长率都是x,写出利润y与增长的百分率x之间的函数解析式,它是二次函数吗?如果是请写出二次项系数、一次项系数和常数项.21. 某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元.
20. 某公司的生产利润原来是a元,经过连续两年的增长达到了y万元,如果每年增长率都是x,写出利润y与增长的百分率x之间的函数解析式,它是二次函数吗?如果是请写出二次项系数、一次项系数和常数项.21. 某产品每件成本28元,在试销阶段产品的日销售量y(件)与每件产品的日销售价x(元)之间的关系如图中的折线所示.为维持市场物价平衡,最高售价不得高出83元.(1)求y与x之间的函数关系式;
(2)要使每日的销售利润w最大,每件产品的日销售价应定为多少元?此时每日销售利润是多少元?
 22. 已知在平面直角坐标系中,抛物线y=﹣+bx+c与x轴相交于点A,B,与y轴相交于点C,直线y=x+4经过A,C两点,
22. 已知在平面直角坐标系中,抛物线y=﹣+bx+c与x轴相交于点A,B,与y轴相交于点C,直线y=x+4经过A,C两点,(1)求抛物线的表达式;
(2)如果点P,Q在抛物线上(P点在对称轴左边),且PQ∥AO,PQ=2AO,求P,Q的坐标;
(3)动点M在直线y=x+4上,且△ABC与△COM相似,求点M的坐标.
 23. 某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
23. 某批发商以每件50元的价格购进400件T恤.若以单价70元销售,预计可售出200件.批发商的销售策略是:第一个月为增加销售量,降价销售,经过市场调查,单价每降低0.5元,可多售出5件,但最低单价不低于购进的价格;第一个月结束后,将剩余的T恤一次性清仓销售,清仓时单价为40元.设第一个月单价降低x元.
(1)根据题意,完成下表:每件T恤的利润(元) 销售量(件) 第一个月 清仓时 (2)T恤的销售单价定为多少元时,该批发商可获得最大利润?最大利润为多少?