（北师大版）2022-2023学年九年级数学下册2.3确定二次函数的表达式同步测试

试卷更新日期：2022-10-24 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

1. 若二次函数y＝ax²＋2ax(a≠0)的图象过点P(1，4)，则该图象必过点（）

A、(－3，4) B、(－1，4) C、(0，3) D、(2，4)

查看试题解析
2. 已知二次函数 $y = (x - \frac{1}{m}) (m x - 4 m)$ （其中m＞0），下列说法正确的是（）

A、当x＞2时，都有y随着x的增大而增大 B、当x＜3时，都有y随着x的增大而减小 C、若x＜n时，都有y随着x的增大而减小，则 $n \geq 2 + \frac{1}{2 m}$ D、若x＜n时，都有y随着x的增大而减小，则 $n \leq 2 + \frac{1}{2 m}$

查看试题解析
3. 如图，已知点A（ $\sqrt{3}$ ，2）， B(0，1)，射线AB绕点A逆时针旋转30°，与x轴交于点C，则过A，B，C三点的二次函数y=ax²+bx+1中a，b的值分别为（）

A、 $a = 2 ， b = - \frac{5}{3} \sqrt{3}$ B、 $a = \frac{1}{2} ， b = - \frac{\sqrt{3}}{6}$ C、 $a = 3 ， b = - \frac{8}{3} \sqrt{3}$ D、 $a = - \frac{1}{3} ， b = \frac{2}{3} \sqrt{3}$

查看试题解析
4. 若二次函数 $y = a x^{2} + 2 a x (a \neq 0)$ 过P(1,4)，则这个函数必过点（）

A、(-3,4) B、(-1,4) C、(0,3) D、(2,4)

查看试题解析
5. 用配方法将y＝ $\frac{1}{2}$ x²+x﹣1写成y＝a（x﹣h）²+k的形式是（）

A、y＝ $\frac{1}{2}$ （x+1）²﹣1 B、y＝ $\frac{1}{2}$ （x﹣1）²﹣1 C、y＝ $\frac{1}{2}$ （x+1）²﹣3 D、y＝ $\frac{1}{2}$ （x+1）²﹣ $\frac{3}{2}$

查看试题解析
6. 如图是一副眼镜镜片下半部分轮廓对应的两条抛物线关于y轴对称．AB∥x轴，AB=4cm，最低点C在x轴上，高CH=1cm，BD=2cm．则右轮廓线DFE所在抛物线的函数解析式为（）

A、y= $\frac{1}{4}$ （x+3）² B、y= $- \frac{1}{4}$ （x+3）² C、y= $\frac{1}{4}$ （x﹣3）² D、y= $- \frac{1}{4}$ （x﹣3）²

查看试题解析
7. 已知点（﹣2，4）在抛物线y=ax²上，则a的值是（）

A、﹣1 B、1 C、±1 D、 $\frac{1}{8}$

查看试题解析
8. 若抛物线的顶点坐标是（﹣2，1）且经过点（1，﹣8），则该抛物线的表达式是（）

A、y=﹣9（x﹣2）²+1 B、y=﹣7（x﹣2）²﹣1 C、y=﹣（x+2）²+1 D、y=﹣ $\frac{7}{9}$ （x+2）²﹣1

查看试题解析
9. 某二次函数，当自变量x满足0≤x≤4时，对应的函数值y满足0≤y≤2，则这个函数不可能是（）

A、y= $\frac{1}{2} {(x - 2)}^{2}$ B、y=x²﹣4x+2 C、y= $- \frac{1}{2} {(x - 2)}^{2}$ +2 D、y=﹣ $\frac{1}{4} x^{2}$ +x+1

查看试题解析
10. 通过配方法将二次函数y=ax²+bx+c（a≠0）化成y=a（x﹣h）²+k的形式，此二次函数可变形为（）

A、y=a（x+ $\frac{b}{2 a}$ ）²+ $\frac{4 a c - b^{2}}{4 a}$ B、y=a（x﹣ $\frac{b}{2 a}$ ）²+ $\frac{4 a c - b^{2}}{4 a}$ C、y=a（x+ $\frac{b}{2 a}$ ）²+ $\frac{b^{2} - 4 a c}{4 a}$ D、y=a（x﹣ $\frac{b}{2 a}$ ）²+ $\frac{b^{2} - 4 a c}{4 a}$

查看试题解析

二、填空题（每题3分，共15分）

11. 如图所示的抛物线是二次函数 $y = a x^{2} - 3 x + a^{2} - 1$ 的图象，那么 $a$ 的值是.

查看试题解析
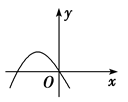12. 如果将抛物线 $y ＝ x^{2} + 2 x ﹣ 1$ 向上平移，使它经过点 $A （ 1 ， 3 ）$ ，那么所得新抛物线的表达式是．

查看试题解析
13. 老师给出一个二次函数，甲、乙、丙三名同学各指出这个函数的一个性质．
甲：函数图象的顶点在x轴上；

乙：当x<1时，y随x的增大而减小；

丙：该函数的开口大小、形状均与函数y=x²的图像相同

已知这三位同学的描述都符合题意，请你写出满足上述所有性质的一个二次函数表达式．

查看试题解析
14. 若抛物线y=ax²+bx+c的顶点是A（2，﹣1），且经过点B（1，0），则抛物线的函数关系式为．

查看试题解析
15. 如图，正方形OABC和正方形CDEF在平面直角坐标系中，点O，C，F在y轴上，点O为坐标原点，点M为OC的中点，抛物线y=ax²+b经过M，B，E三点，则 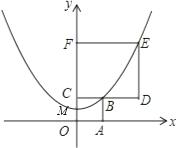$\frac{F E}{C B}$ 的值为．

查看试题解析

三、解答题（共8题，共55分）

16. 如图，已知直钱 $y = \frac{1}{2} x + 1$ 与y轴交于点A，与x轴交于点D，抛物线 $y = \frac{1}{2} x^{2} + b x + c$ 与直线 $y = \frac{1}{2} x + 1$ 交于A，E两点，与x轴交于B，C两点，点B的坐标为 $(1 ， 0)$ ，求该抛物线对应的函数表达式.

查看试题解析
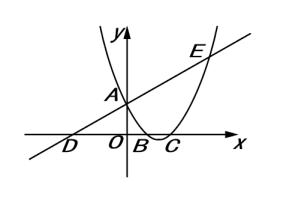17. 已知二次函数 $y = - \frac{3}{16} x^{2} + b x + c$ 的图象经过 $A (0 ， 3)$ ， $B (- 4 ， - \frac{9}{2})$ 两点，求b，c的值.

查看试题解析
18. 如图，已知二次函数y=ax²+2x+c的图象经过点C（0，3），与x轴分别交于点A，点B（3，0）。点P是直线BC上方的抛物线上一动点

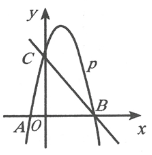(1)、求二次函数y=ax²+2x+c的表达式；

(2)、连接PO，PC，并把△POC沿y轴翻折，得到四边形POPC.若四边形POP'C为菱形，请求出此时点P的坐标；

(3)、当点P运动到什么位置时，四边形ACPB的面积最大？求出此时P点的坐标和四边形ACPB的最大面积.

查看试题解析
19. 已知：二次函数y=ax ²+bx+c（a≠0）的图象如图所示．请你根据图象提供的信息，求出这条抛物线的表达式．

查看试题解析
20. 抛物线y₁=x²+bx+c与直线y₂=﹣2x+m相交于A（﹣2，n）、B（2，﹣3）两点．求这条抛物线的解析式．

查看试题解析
21. 二次函数y= $\frac{1}{2}$ （x+h）²的图象如图所示，已知OA=OC，试求该抛物线的解析式．

查看试题解析
22. 已知二次函数图象顶点坐标（﹣3， $\frac{1}{2}$ ）且图象过点（2， $\frac{11}{2}$ ），求二次函数解析式及图象与y轴的交点坐标．

查看试题解析
23. 已知二次函数y=ax²+bx的图象过点（2，0），（﹣1，6）．
（1）求二次函数的关系式；
（2）写出它的对称轴和顶点坐标；
（3）请说明x在什么范围内取值时，函数值y＜0？

查看试题解析

（北师大版）2022-2023学年九年级数学下册2.3确定二次函数的表达式 同步测试

一、单选题（每题3分，共30分）

二、填空题（每题3分，共15分）

三、解答题（共8题，共55分）

（北师大版）2022-2023学年九年级数学下册2.3确定二次函数的表达式同步测试