(北师大版)2022-2023学年九年级数学下册第一章 直角三角形的边角关系 单元测试
试卷更新日期:2022-10-24 类型:单元试卷
一、单选题(每题3分,共30分)
-
1. 在 中, , , ,则 的值为( )A、 B、 C、 D、2. 如图,A、B、C是小正方形的顶点,且每个小正方形的边长为1,则tan∠BAC的值为( )
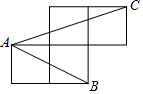 A、 B、1 C、 D、3. 若 ,则 的大小是( )A、30° B、45° C、60° D、75°4. 为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )
A、 B、1 C、 D、3. 若 ,则 的大小是( )A、30° B、45° C、60° D、75°4. 为了方便行人推车过某天桥,市政府在10m高的天桥一侧修建了40m长的斜道(如图所示),我们可以借助科学计算器求这条斜道倾斜角的度数,具体按键顺序是( )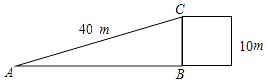 A、
A、 B、
B、 C、
C、 D、
D、 5. 如图,将长、宽分别为6cm, cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )
5. 如图,将长、宽分别为6cm, cm的长方形纸片分别沿AB,AC折叠,点M,N恰好重合于点P.若∠α=60°,则折叠后的图案(阴影部分)面积为( )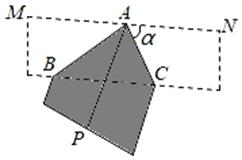 A、 cm2 B、(36 )cm2 C、 cm2 D、 cm26. 一辆汽车在坡角为 的坡面上行驶1000米,则它上升的高度为( )米A、 B、 C、 D、7. 在台风来临之前,有关部门用钢管加固树木(如图),固定点A离地面的高度AC=m,钢管与地面所成角∠ABC=∠ ,那么钢管AB的长为( )
A、 cm2 B、(36 )cm2 C、 cm2 D、 cm26. 一辆汽车在坡角为 的坡面上行驶1000米,则它上升的高度为( )米A、 B、 C、 D、7. 在台风来临之前,有关部门用钢管加固树木(如图),固定点A离地面的高度AC=m,钢管与地面所成角∠ABC=∠ ,那么钢管AB的长为( )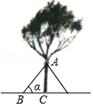 A、m•sin B、m•cos C、 D、8. 如图,在河流两边有甲、乙两座山,现在从甲山A处的位置向乙山B处拉电线,已知甲山AC的坡比为15:8.乙山BD的坡比为4:3,甲山上A点到河边c的距离AC=340米,乙山上B点到河边D的距离BD=900米,从B处看A处的俯角为26°,则河CD的宽度是(参考值:sin26°=0.4383,tan26°=0.4788,co26°=0.8988)结果精确到0.01)( )
A、m•sin B、m•cos C、 D、8. 如图,在河流两边有甲、乙两座山,现在从甲山A处的位置向乙山B处拉电线,已知甲山AC的坡比为15:8.乙山BD的坡比为4:3,甲山上A点到河边c的距离AC=340米,乙山上B点到河边D的距离BD=900米,从B处看A处的俯角为26°,则河CD的宽度是(参考值:sin26°=0.4383,tan26°=0.4788,co26°=0.8988)结果精确到0.01)( ) A、177.19米 B、188.85米 C、192.0米 D、258.25米9. 直角梯形ABCD如图放置,AB、CD为水平线,BC⊥AB,如果∠BCA=67°,从低处A处看高处C处,那么点C在点A的( )
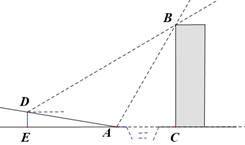
A、177.19米 B、188.85米 C、192.0米 D、258.25米9. 直角梯形ABCD如图放置,AB、CD为水平线,BC⊥AB,如果∠BCA=67°,从低处A处看高处C处,那么点C在点A的( )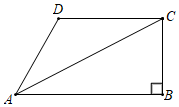 A、俯角67°方向 B、俯角23°方向 C、仰角67°方向 D、仰角23°方向10. 如图,某一时刻,小宁站在斜坡AC上的A处,小李在大楼FD的楼顶F处,此时小宁望小李的仰角为18.43°.5秒后,小宁沿斜坡AC前进到达C处,小李从大楼F处下楼到大楼E处,此时小李望小宁的俯角为22.6°;然后小李继续下楼,小宁沿CD前往楼底D处,已知小宁的速度为5.2米/秒,大楼FD的高度为30米,斜坡AC的坡度为1:2.4,小李、小宁都保持匀速前进,若斜坡、大楼在同一平面内,小李、小宁的身高忽略不计,则当小李达到楼底D处时,小宁距离D处的距离为( )米.
A、俯角67°方向 B、俯角23°方向 C、仰角67°方向 D、仰角23°方向10. 如图,某一时刻,小宁站在斜坡AC上的A处,小李在大楼FD的楼顶F处,此时小宁望小李的仰角为18.43°.5秒后,小宁沿斜坡AC前进到达C处,小李从大楼F处下楼到大楼E处,此时小李望小宁的俯角为22.6°;然后小李继续下楼,小宁沿CD前往楼底D处,已知小宁的速度为5.2米/秒,大楼FD的高度为30米,斜坡AC的坡度为1:2.4,小李、小宁都保持匀速前进,若斜坡、大楼在同一平面内,小李、小宁的身高忽略不计,则当小李达到楼底D处时,小宁距离D处的距离为( )米.(已知:tan18.43°≈ ,sin18.43°≈ ,cos22.6°≈ ,tan22.6≈ )
 A、10 B、15.6 C、20.4 D、26
A、10 B、15.6 C、20.4 D、26二、填空题(每题3分,共15分)
-
11. 如图,为了测量电线杆AB的高度,小明将测量仪放在与电线杆的水平距离为9m的D处.若测角仪CD的高度为1.5m,在C处测得电线杆顶端A的仰角为36°,则电线杆AB的高度约为(精确到0.1m).(参考数据sin36°≈0.59.cos36°≈0.81,tan36°≈0.73).
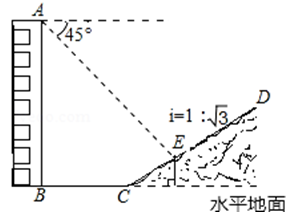
 12. 已知传送带与水平面所成斜坡的坡度i=1∶2.4,如果它把物体送到离地面5米高的地方,那么物体所经过的路程为米.13. 有一拦水坝的横断面是等腰梯形,它的上底长为6米,下底长为10米,高为2 米,那么此拦水坝的坡角为度.
12. 已知传送带与水平面所成斜坡的坡度i=1∶2.4,如果它把物体送到离地面5米高的地方,那么物体所经过的路程为米.13. 有一拦水坝的横断面是等腰梯形,它的上底长为6米,下底长为10米,高为2 米,那么此拦水坝的坡角为度.
14. 如图,在一次数学课外实践活动中,小聪在距离旗杆10m的A处测得旗杆顶端B的仰角为60°,测角仪高AD为1m,则旗杆高BC为m.(结果保留根号)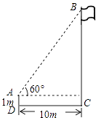 15. 如图,已知斜坡 AB 的坡度为 3∶4.若坡长 AB=10m,则坡高 BC=m.
15. 如图,已知斜坡 AB 的坡度为 3∶4.若坡长 AB=10m,则坡高 BC=m.
三、解答题(共8题,共55分)
-
16. 如图,在4×8的矩形网格中,每个小正方形的边长都为1,△ABC的三个顶点都在格点上,求tan∠BAC的值.
 17. 先化简,再求代数式的值,其中 .18. (1)验证下列两组数值的关系:
17. 先化简,再求代数式的值,其中 .18. (1)验证下列两组数值的关系:2sin30°•cos30°与sin60°;
2sin22.5°•cos22.5°与sin45°.
(2)用一句话概括上面的关系.
(3)试一试:你自己任选一个锐角,用计算器验证上述结论是否成立.
(4)如果结论成立,试用α表示一个锐角,写出这个关系式.
19. 如图,在△ABC中,∠B=90°, ,D是 上的一点,连结 ,若∠BDC=60°,BD= .试求AC的长. 20. 如图,在△ABC中,AB=2 ,AC=4,∠B=45°,求BC的长.
20. 如图,在△ABC中,AB=2 ,AC=4,∠B=45°,求BC的长.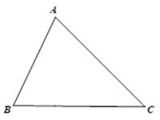 21. 如图1是1副创意卡通圆规,图2是其平面示意图, 是支撑臂, 是旋转臂,使用时,以 为支撑点,铅笔芯端点 可绕点 旋转作出圆.已知 ,当 时,所作圆的半径为 ;保持 不变,在旋转臂 末端的铅笔芯折断了一截的情况下,作出的圆半径仍为 ,求铅笔芯折断部分的长度.(参考数据: , ,结果精确到 )
21. 如图1是1副创意卡通圆规,图2是其平面示意图, 是支撑臂, 是旋转臂,使用时,以 为支撑点,铅笔芯端点 可绕点 旋转作出圆.已知 ,当 时,所作圆的半径为 ;保持 不变,在旋转臂 末端的铅笔芯折断了一截的情况下,作出的圆半径仍为 ,求铅笔芯折断部分的长度.(参考数据: , ,结果精确到 )