(北师大版)2022-2023学年九年级数学下册1.4 解直角三角形 同步测试
试卷更新日期:2022-10-24 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 如图,若△ABC底边BC上的高为h1 , △DEF底边EF上的高为h2 , 则h1与h2的大小关系是( )
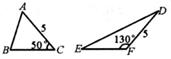 A、h1=h2 B、h1<h2 C、h1>h2 D、以上都有可能2. 如图,是电杆的一根拉线,测得米, , 则拉线的长为( )
A、h1=h2 B、h1<h2 C、h1>h2 D、以上都有可能2. 如图,是电杆的一根拉线,测得米, , 则拉线的长为( )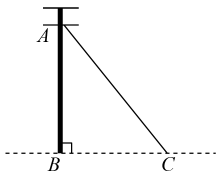 A、米 B、米 C、米 D、米3. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )
A、米 B、米 C、米 D、米3. 图1是第七届国际数学教育大会(ICME)的会徽,在其主体图案中选择两个相邻的直角三角形,恰好能组合得到如图2所示的四边形OABC .若 AB=BC=1,∠AOB=α,则 OC2的值为( )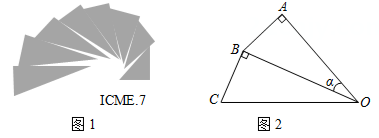 A、 B、 C、 D、4. 在 中,∠C= ,AB=4, ,则 的长为( )A、3 B、2 C、 D、5. 如图,在△ABC中,∠C=90°,∠A=30°,BD为△ABC的角平分线,若AC=12,则在△ABD中AB边上的高为( )
A、 B、 C、 D、4. 在 中,∠C= ,AB=4, ,则 的长为( )A、3 B、2 C、 D、5. 如图,在△ABC中,∠C=90°,∠A=30°,BD为△ABC的角平分线,若AC=12,则在△ABD中AB边上的高为( ) A、3 B、4 C、5 D、66. 如图1,点P从 的顶点A出发,沿A→C→B的路径匀速运动到点B停止,作PQ⊥AB于点Q,设点P运动的路程为x,PQ的长为y,若y与x之间的函数关系如图2所示,当x=6时,PQ的长为( )
A、3 B、4 C、5 D、66. 如图1,点P从 的顶点A出发,沿A→C→B的路径匀速运动到点B停止,作PQ⊥AB于点Q,设点P运动的路程为x,PQ的长为y,若y与x之间的函数关系如图2所示,当x=6时,PQ的长为( )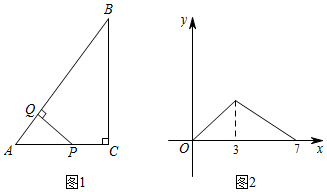 A、1 B、 C、 D、7. 如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把 BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为( )
A、1 B、 C、 D、7. 如图,矩形ABCD中,AB=3,BC=4,点E是AB边上一点,且AE=2,点F是边BC上的任意一点,把 BEF沿EF翻折,点B的对应点为G,连接AG,CG,则四边形AGCD的面积的最小值为( ) A、 B、 C、 D、88. 在Rt△ABC中,∠C=90°,sinA= ,BC=6,则AB长是( )A、4 B、6 C、8 D、109. 如图,线杆DC的高度为 ,两根拉线 与 互相垂直, ,若 、 、 在同一条直线上,则拉线 的长度为( )
A、 B、 C、 D、88. 在Rt△ABC中,∠C=90°,sinA= ,BC=6,则AB长是( )A、4 B、6 C、8 D、109. 如图,线杆DC的高度为 ,两根拉线 与 互相垂直, ,若 、 、 在同一条直线上,则拉线 的长度为( ) A、 B、 C、 D、10. 如图,直线 与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△ ,则点 的坐标是( )
A、 B、 C、 D、10. 如图,直线 与x轴、y轴分别交于A、B两点,把△AOB绕点A顺时针旋转60°后得到△ ,则点 的坐标是( )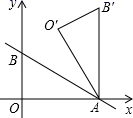 A、( ,4) B、(4, ) C、( ,3) D、( +2, )
A、( ,4) B、(4, ) C、( ,3) D、( +2, )二、填空题(每题3分,共15分)
-
11. 将一架长为3米的梯子斜靠在竖直的墙AB上,梯子与地面的夹角 , 则梯子底端C与墙根A点的距离为米.(结果精确到米)[参考数据: , , ]
 12. 在中, , 点P在直线上,点P到直线的距离为 , 则的长为 .13. 两幅大小不同的三角板中各取一个,如图1叠放(直角顶点重合), , ,且 ,把 绕点 顺时针旋转45°后, 交 于点 ,则 .
12. 在中, , 点P在直线上,点P到直线的距离为 , 则的长为 .13. 两幅大小不同的三角板中各取一个,如图1叠放(直角顶点重合), , ,且 ,把 绕点 顺时针旋转45°后, 交 于点 ,则 . 14. 如图,在菱形ABCD中,tanA= ,M , N分别在AD , BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D , 当EF⊥AD时, 的值为 .
14. 如图,在菱形ABCD中,tanA= ,M , N分别在AD , BC上,将四边形AMNB沿MN翻折,使AB的对应线段EF经过顶点D , 当EF⊥AD时, 的值为 . 15. 在中,若AB= AC,则 =
15. 在中,若AB= AC,则 =三、解答题(共8题,共55分)
-
16. 如图,在△ABC中,∠C=90°,AB=10,sinB= 。求BC的长及∠A的正切值.
 17. 共享单车为大众出行提供了方便,图1为单车实物图,图2为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知∠ABE=70°,∠EAB=45°,车轮半径为30cm,BE=40cm.小明体验后觉得当坐垫C离地面高度为90cm时骑着比较舒适,求此时CE的长.(结果精确到1cm)(参考数据: , , , )
17. 共享单车为大众出行提供了方便,图1为单车实物图,图2为单车示意图,AB与地面平行,点A、B、D共线,点D、F、G共线,坐垫C可沿射线BE方向调节.已知∠ABE=70°,∠EAB=45°,车轮半径为30cm,BE=40cm.小明体验后觉得当坐垫C离地面高度为90cm时骑着比较舒适,求此时CE的长.(结果精确到1cm)(参考数据: , , , ) 18. 在一次数学活动课上,数学老师在同一平面内将一副直角三角板如图位置摆放,点C在 的延长线上, , , , , ,试求 的长.
18. 在一次数学活动课上,数学老师在同一平面内将一副直角三角板如图位置摆放,点C在 的延长线上, , , , , ,试求 的长. 19. 南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业、当渔船航行至B处时,测得该岛位于正北方向20(1+ )海里的C处,为了防止某国海运警干扰,就请求我4处的渔监船前往C处护航,已知C位于4处的北偏东45°方向上。A位于B的北偏西30°的方向上,求A、C之间的距离。
19. 南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业、当渔船航行至B处时,测得该岛位于正北方向20(1+ )海里的C处,为了防止某国海运警干扰,就请求我4处的渔监船前往C处护航,已知C位于4处的北偏东45°方向上。A位于B的北偏西30°的方向上,求A、C之间的距离。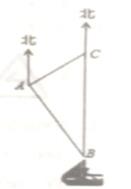 20. 在Rt△ABC中,a,b,c分别是∠A,∠B,∠C的对边,∠C=90°,a+b=4,且tanB=1,求c的长.
20. 在Rt△ABC中,a,b,c分别是∠A,∠B,∠C的对边,∠C=90°,a+b=4,且tanB=1,求c的长.
21. 如图,在Rt△ABC中,∠ACB=90°,D是AB的中点,过D点作AB的垂线交AC于点E,BC=6,sin A= ,求DE的长度. 22. 如图,在△ABC中,∠BCA=90°,BC=1.5,点F,A,C在同一直线上,∠BAC=30°,DE⊥AB于点D,BE与AB的夹角∠EBD=60°,AD=1,过E点作AC的垂线,交AC的反向延长线于F.求BE及EF的长.
22. 如图,在△ABC中,∠BCA=90°,BC=1.5,点F,A,C在同一直线上,∠BAC=30°,DE⊥AB于点D,BE与AB的夹角∠EBD=60°,AD=1,过E点作AC的垂线,交AC的反向延长线于F.求BE及EF的长. 23. 阅读理解题:下面利用45°角的正切,求tan22.5°的值,方法如下:
23. 阅读理解题:下面利用45°角的正切,求tan22.5°的值,方法如下:解:构造Rt△ABC,其中∠C=90°,∠B=45°,如图.
延长CB到D,使BD=AB,连接AD,则∠D= ∠ABC=22.5°.
设AC=a,则BC=a,AB=BD= a.
又∵CD=BD+CB=(1+ )atan22.5°=tan∠D= ﹣1
请你仿照此法求tan15°的值.
