(北师大版)2022-2023学年九年级数学下册1.2 30°、45°、60°角的三角函数值 同步测试
试卷更新日期:2022-10-24 类型:同步测试
一、单选题(每题3分,共30分)
-
1. 实数 , , , , , , (相邻两个3之间依次多一个 1) ,其中无理数的个数是( )A、4 B、2 C、1 D、32. 已知α是锐角,若sinα= ,则α的度数是( )A、30° B、45° C、60° D、75°3. 计算sin 45°+cos45°的值为( )A、1 B、2 C、 D、24. 如图,在△ABC中,点D是AB中点,BE⊥AC垂足为E , 连接DE , 若∠ABE=30°,∠C=45°,DE=2,则BC的长为( )
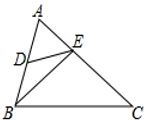 A、2 B、3 C、2 D、25. 在△ABC中,(2cosA- )2+| -tanB|=0,则△ABC一定是( )A、直角三角形 B、钝角三角形 C、等腰三角形 D、锐角三角形6. 若规定 ,则sin15°=( )A、 B、 C、 D、7. 已知 为锐角,且 ,则 等于( )A、 B、 C、 D、8. 计算2cos60° -sin245°+cot60°的结果是( )A、 B、 C、 D、9. 如图是一个 的方阵,其中每行,每列的两数和相等,则a可以是( )
A、2 B、3 C、2 D、25. 在△ABC中,(2cosA- )2+| -tanB|=0,则△ABC一定是( )A、直角三角形 B、钝角三角形 C、等腰三角形 D、锐角三角形6. 若规定 ,则sin15°=( )A、 B、 C、 D、7. 已知 为锐角,且 ,则 等于( )A、 B、 C、 D、8. 计算2cos60° -sin245°+cot60°的结果是( )A、 B、 C、 D、9. 如图是一个 的方阵,其中每行,每列的两数和相等,则a可以是( )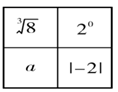 A、 B、 C、0 D、10. 如图,某天然气公司的主输气管道从A市的北偏东 方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东 方向,测绘员由A处沿主输气管道步行1000米到达点C处,测得M小区位于点C的北偏西 方向,试在主输气管道上寻找支管道连接点N,使点N到该小区铺设的管道最短,此时铺设的管道的最短距离约是( ).
A、 B、 C、0 D、10. 如图,某天然气公司的主输气管道从A市的北偏东 方向直线延伸,测绘员在A处测得要安装天然气的M小区在A市的北偏东 方向,测绘员由A处沿主输气管道步行1000米到达点C处,测得M小区位于点C的北偏西 方向,试在主输气管道上寻找支管道连接点N,使点N到该小区铺设的管道最短,此时铺设的管道的最短距离约是( ).(参考数据: , )
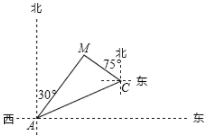 A、366米 B、650米 C、634米 D、700米
A、366米 B、650米 C、634米 D、700米二、填空题(每题3分,共15分)
-
11. .12. 计算tan 45°的正确结果是 .13. 如图,在菱形 中, 为 边上的高,将 沿 所在的直线翻折,得到 ,若 ,则菱形的边长为 .
 14. 在△ABC中,∠B=45°,cosA= ,则∠C的度数是.15. 如图,半圆的直径 点C在半圆上, ,则阴影部分的面积为(结果保留 ).
14. 在△ABC中,∠B=45°,cosA= ,则∠C的度数是.15. 如图,半圆的直径 点C在半圆上, ,则阴影部分的面积为(结果保留 ).
三、解答题(共8题,共55分)
-
16. 先化简,再求值: , 其中.17. 先化简 , 然后再从sin30°,1,这三个数中选取一个你认为合适的数作为a的值代入求值.18. 先化简,再求值: , 其中.19. 如图,两幢楼高AB=CD=30m,两楼间的距离AC=24m,当太阳光线与水平线的夹角为30°时,求甲楼投在乙楼上的影子的高度.(结果精确到0.01, ≈1.732, ≈1.414)
 20. 如图,已知△ABC中,∠C=90°,且sinA= ,BC=1.5,求AC.
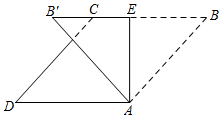
20. 如图,已知△ABC中,∠C=90°,且sinA= ,BC=1.5,求AC. 21. 在一次暑假旅游中,小亮在仙岛湖的游船上(A处),测得湖西岸的山峰太婆尖(C处)和湖东岸的山峰老君岭(D处)的仰角都是45°.游船向东航行100米后(B处),测得太婆尖,老君岭的仰角分别为30°,60°.试问太婆尖、老君岭的高度为多少米?
21. 在一次暑假旅游中,小亮在仙岛湖的游船上(A处),测得湖西岸的山峰太婆尖(C处)和湖东岸的山峰老君岭(D处)的仰角都是45°.游船向东航行100米后(B处),测得太婆尖,老君岭的仰角分别为30°,60°.试问太婆尖、老君岭的高度为多少米? 22. (1)计算:;
22. (1)计算:;(2)先化简,再求值:(a﹣2)(a+2)﹣a(a﹣2),其中a=﹣1.
23. 小明在某次作业中得到如下结果:sin27°+sin283°≈0.122+0.992=0.9945,
sin222°+sin268°≈0.372+0.932=1.0018,
sin229°+sin261°≈0.482+0.872=0.9873,
sin237°+sin253°≈0.602+0.802=1.0000,
sin245°+sin245°=( )2+( )2=1.
据此,小明猜想:对于任意锐角α,均有sin2α+sin2(90°﹣α)=1.
(Ⅰ)当α=30°时,验证sin2α+sin2(90°﹣α)=1是否成立;
(Ⅱ)小明的猜想是否成立?若成立,请给予证明;若不成立,请举出一个反例.