（北师大版）2022-2023学年九年级数学下册1.1 锐角三角形同步测试

试卷更新日期：2022-10-24 类型：同步测试

进入出卷网下载

一、单选题（每题3分，共30分）

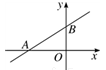
1. 如图，直线y= $\frac{3}{4}$ x+3与x轴，y轴分别相交于A、B两点，则cos∠BAO的值是（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{4}{3}$ D、 $\frac{5}{4}$

查看试题解析
2. 如图，在△ABC中，AB＝AC，BC＝8，E为AC边的中点，线段BE的垂直平分线交边BC于点D.设BD＝x，tan∠ACB＝y，则x与y满足关系式（　　）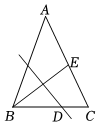

A、x﹣y²＝3 B、2x﹣y²＝6 C、3x﹣y²＝9 D、4x﹣y²＝12

查看试题解析
3. 如图，等边 $△ A B C$ 边长为 $4 \sqrt{3}$ ， $∠ A B C$ 和 $∠ A C B$ 的角平分线相交于点O，将 $△ O B C$ 绕点O逆时针旋转 $30 °$ 得到 $△ O B_{1} C_{1}$ ， $B_{1} C_{1}$ 交BC于点D， $B_{1} C_{1}$ 交AC于点E，则DE=（）

A、2 B、 $6 - 2 \sqrt{3}$ C、 $\sqrt{3} - 1$ D、 $3 - \sqrt{3}$

查看试题解析
4. 在Rt $△ A B C$ 中， $∠ C = 90 °$ ，若 $B C = 3$ ， $A C = 4$ ，则 $c o s B$ 的值为（）

A、 $\frac{4}{5}$ B、 $\frac{3}{5}$ C、 $\frac{3}{4}$ D、 $\frac{4}{3}$

查看试题解析
5. 如图，已知在矩形ABCD中，M是AD边的中点，BM与AC垂直，交直线AC于点N，连接DN，则下列四个结论中：①CN＝2AN；②DN＝DC；③tan∠CAD＝ $\sqrt{2}$ ；④△AMN∽△CAB.正确的有（）

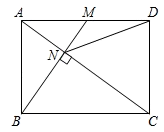A、①②③④ B、①②③ C、①②④ D、②③④

查看试题解析
6. 如图，在菱形ABCD中，DE⊥AB，cosA＝ $\frac{3}{5}$ ， AE＝3，则tan∠DBE的值是（）

A、 $\frac{1}{2}$ B、2 C、 $\frac{\sqrt{5}}{2}$ D、 $\frac{\sqrt{5}}{5}$

查看试题解析
7. 如图，在 $△ A B C$ 中， $∠ C = 90 °$ ， $A B = 5$ ， $A C = 4$ ，下列三角函数表示正确的是（）

A、 $s i n A = \frac{4}{5}$ B、 $c o s A = \frac{4}{5}$ C、 $t a n A = \frac{4}{3}$ D、 $t a n B = \frac{4}{5}$

查看试题解析
8. 如图，在Rt△ABC中，∠A＝90°，AB＝8，BC＝10，则cosB的值是（）

A、 $\frac{3}{4}$ B、 $\frac{4}{3}$ C、 $\frac{3}{5}$ D、 $\frac{4}{5}$

查看试题解析
9. 如图所示，正方形ABCD中， $A B = 4$ ，点E为BC中点， $B F ⊥ A E$ 于点G，交CD边于点F，连接DG，则DG长为（）

A、 $\frac{9}{5} \sqrt{5}$ B、4 C、 $\frac{16}{5}$ D、 $\frac{8}{5} \sqrt{5}$

查看试题解析
10. 如图，菱形ABCD的顶点分别在反比例函数y = $\frac{k_{1}}{x}$ 和y= $\frac{k_{2}}{x}$ 的图象上，若∠BCD=60°，则 $\frac{k_{1}}{k_{2}}$ 的值是（）

A、- $\frac{1}{3}$ B、- $\frac{2}{3}$ C、- $\frac{\sqrt{3}}{3}$ D、- $\sqrt{3}$

查看试题解析

二、填空题（每题3分，共15分）

11. 如图，在△ABC中，AC＝6，BC＝8，点D、E分别在AC、BC上，点F在△ABC内．若四边形CDFE是边长为2的正方形，则cos∠ABF＝．

查看试题解析
12. 如图，在Rt△ABC中，∠C＝90°，AC＝6，BC＝8，将 $△ A B C$ 绕点A逆时针旋转得到 $△ A B^{'} C^{'}$ ，使点 $C^{'}$ 落在AB边上，连结 $B B^{'}$ ，则 $s i n ∠ B B^{'} C^{'}$ 的值为.

查看试题解析
13. 如图，线段AB＝10，点D是线段AB上的一个动点（不与点A重合），在AB上方作以AD为腰的等腰△ACD，且∠CAD＝120°，过点D作射线DP⊥CD，过DP上一动点G（不与D重合）作矩形CDGH，其对角线交点为O，连接OB，则线段OB的最小值为．

查看试题解析
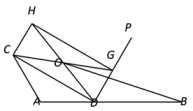14. 如图，在Rt△ABC中，∠ACB= 90°，CD⊥AB于点D， AD= $\frac{9}{5}$ ， BD= $\frac{16}{5}$ ，则sinB=.

查看试题解析
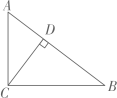15. 如图，Rt△AOB中，∠OAB＝90°，∠OBA＝30°，顶点A在反比例函数y＝ $- \frac{4}{x}$ 图象上，若Rt△AOB的面积恰好被y轴平分，则进过点B的反比例函数的解析式为.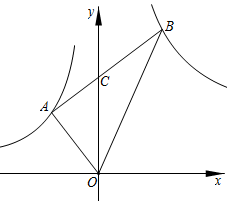

查看试题解析

三、解答题（共8题，共55分）

16. 如图，AB是垂直于水平面的建筑物.为测量AB的高度，小红从建筑物底端B点出发，沿水平方向行走了5.2米到达点C，然后沿斜坡CD前进，到达坡顶D点处，DC=BC．在点D处放置测角仪，测角仪支架DE高度为0.8米，在E点处测得建筑物顶端A点的仰角∠AEF为27°(点A，B，C，D，E在同一平面内).斜坡CD的坡度(或坡比)i=1：2.4，求建筑物AB的高度.(参考数据sin27°≈0.45，cos27°≈0.89，tan27°≈0.51)

查看试题解析
17. 如图所示，Rt△ABC中，∠C＝90°，点D、E分别在AC、AB上，BD平分∠ABC，DE⊥AB，cotA＝ $\frac{3}{4}$ ，求tan∠DBC的值.

查看试题解析
18. 如图，四边形ABCD中，∠ADB=∠DBC=90°，AD=6，CD=12，tanA= $\frac{4}{5}$ ，求sinC的值．

查看试题解析
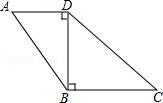19. 如图，将矩形ABCD沿CE折叠，点B恰好落在边AD上的点F处，如果 $\frac{A B}{B C} = \frac{2}{3}$ 求tan∠DCF的值.

查看试题解析
20. 如图，在Rt△ABC中，∠C=90°，∠A、∠B、∠C的对边分别是a、b、c，我们把∠A的邻边与斜边的比叫做∠A的余弦，记作cosA，即cosA= $\frac{b}{c}$ ．当c=2，a=1时，求cosA．

查看试题解析
21. 如图，在Rt△ABC中，∠C=90°，M是直角边AC上一点，MN⊥AB于点N，AN=3，AM=4，求cosB的值．

查看试题解析
22. 在Rt△ABC中，∠ACB=90°，AC=3，tanB= $\frac{4}{3}$ ，求AB的值．

查看试题解析
23.
如图，在平面直角坐标系中，已知点B（4，2），BA⊥x轴于A．
（1）求tan∠BOA的值；
（2）将点B绕原点逆时针方向旋转90°后记作点C，求点C的坐标．

查看试题解析

（北师大版）2022-2023学年九年级数学下册1.1 锐角三角形 同步测试

一、单选题（每题3分，共30分）

二、填空题（每题3分，共15分）

三、解答题（共8题，共55分）

（北师大版）2022-2023学年九年级数学下册1.1 锐角三角形同步测试