（人教版）2022-2023学年九年级数学下册第27章相似同步测试

试卷更新日期：2022-10-24 类型：单元试卷

进入出卷网下载

一、单选题

1. 手工制作课上，小丽利用一些花布的边角料，剪裁后装饰手工画，如图，下面四个图案是她剪裁出的空心的直角三角形、等边三角形、正方形、矩形花边，其中，每个图案花边的宽度都相等，那么，每个图案中花边的内外边缘所围成的几何图形不相似的是（）

A、 B、 C、 D、

查看试题解析
2. 下列说法不一定正确的是（　　）

A、所有的等边三角形都相似 B、所有的等腰直角三角形都相似 C、所有的菱形都相似 D、所有的正方形都相似

查看试题解析
3. 如图，AB是⊙O的直径，CD⊥AB于点E，连结CO并延长，交弦AD于点F．若AB=10，BE=2，则OF的长度是（）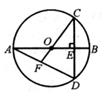

A、 $\frac{5}{2}$ B、3 C、 $\frac{25}{11}$ D、 $\sqrt{5}$

查看试题解析
4. 如图， $A B ∥ C D ， A E ∥ F D$ ， $A E$ ， $F D$ 分别交 $B C$ 于点G，H，则下列结论中不正确的是（）

A、 $\frac{D H}{F H} = \frac{C H}{B H}$ B、 $\frac{G E}{D F} = \frac{C G}{C B}$ C、 $\frac{A F}{A G} = \frac{B F}{F A}$ D、 $\frac{F H}{A G} = \frac{B F}{F A}$

查看试题解析
5. 如图所示，在平行四边形ABCD中，点E为BC中点，连接DE，过点A作 $A F ⊥ C D$ 于点F，交DE于点G，连接BG并延长交CD于点H，恰好使 $D H ： H C = 2 ： 3$ .已知 $A B = 5$ ，阴影部分△BEG的面积为3，则AG的长度是（）

A、 $\frac{18}{5}$ B、4 C、 $\frac{22}{5}$ D、 $\frac{24}{5}$

查看试题解析
6. 如图，在△ABC中，∠ACB＝2∠B，CD平分∠ACB，AD＝2，BD＝3，则AC的长为（）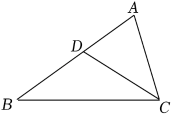

A、3 B、 $\sqrt{10}$ C、4 D、 $2 \sqrt{3}$

查看试题解析
7. 如图，某人拿着一把分度值为厘米的刻度尺，站在距电线杆 $25 m$ 的地方，手臂向前伸直，将刻度尺竖直，看到刻度尺上 $14 c m$ 的长度恰好遮住电线杆．已知臂长为 $70 c m$ ，则电线杆的高是（）．

A、 $5 m$ B、 $6 m$ C、 $125 m$ D、 $4 m$

查看试题解析
8. 如图，身高为1.6m的某学生想测量一棵大树的高度，她沿着树影BA由B到A走去，当走到C点时，她的影子顶端正好与树的影子顶端重合，测得BC=3.2m，CA=0.8m，则树的高度为（）

A、4.8m B、6.4m C、8m D、10m

查看试题解析
9. 如图，在平面直角坐标系中， $△ A B C$ 的顶点坐标分别是 $A (2 ， 2)$ ， $B (4 ， 2)$ ， $C (4 ， 4)$ ，以原点为位似中心，在原点的异侧画 $△ D E F$ ，使 $△ D E F$ 与 $△ A B C$ 成位似图形，且相似比为 $1 ： 2$ ，则线段DF的长度为（）

A、 $\sqrt{2}$ B、2 C、 $2 \sqrt{2}$ D、4

查看试题解析
10. 如图，△ABO三个顶点的坐标分别为A（4，﹣5），B（6，0），0（0，0），以原点O为位似中心，把这个三角形放大为原来的2倍，得到△A′B′O′，则点A的对应点A′的坐标是（）

A、（8，﹣10） B、（﹣8，10） C、（8，﹣10）或（﹣8，10） D、（8，﹣10）或（4，5）

查看试题解析

二、填空题

11.
如图所示，一般书本的纸张是原纸张多次对开得到的，矩形ABCD沿EF对开后，再把矩形EFCD沿MN对开，依次类推，若各种开本的矩形都相似，那么 $\frac{A B}{A D}$ = ．

查看试题解析
12. 如图，直角三角形纸片ABC，AC边长为10cm，现从下往上依次裁剪宽为4cm的矩形纸条，若剪得第二张矩形纸条恰好是正方形，那么BC的长度是cm.

查看试题解析
13. 如图，在矩形ABCD中，AB=15，AD=20，P是AD边上不与A和D重合的一个动点，过点P分别作AC和BD的垂线，垂足为E和F，则PE·PF的最大值为

查看试题解析
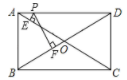14. 图1是装了液体的高脚杯示意图（数据如图），用去一部分液体后如图2所示，此时液面AB= cm

查看试题解析
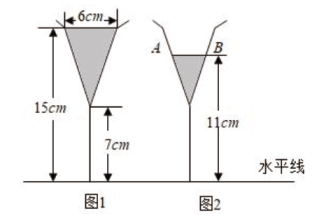15. 如图，△ABC与△A'B'C'是以坐标原点O为位似中心的位似图形，且 $\frac{O A}{O A'}$ = $\frac{1}{2}$ ，已知点A（﹣1，0），点C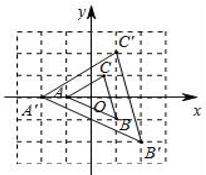（ $\frac{1}{2}$ ，1），则A'C'=.

查看试题解析

三、解答题

16.
已知：Rt△OAB在直角坐标系中的位置如图所示，P（3，4）为OB的中点，点C为折线OAB上的动点，线段PC把Rt△OAB分割成两部分. 问：点C在什么位置时，分割得到的三角形与Rt△OAB相似？（注：在图上画出所有符合要求的线段PC，并写出相应的点C的坐标）．

查看试题解析
17.
如果一个图形经过分割，能成为若干个与自身相似的图形，我们称它为“相似分割的图形”，如图所示的等腰直角三角形和矩形就是能相似分割的图形.

(1)你能否再各举出一个 “能相似分割”的三角形和四边形？
(2)一般的三角形是否是“能相似分割的图形”？如果是请给出一种分割方案并画出图形，否则说明理由.

查看试题解析
18. 如图，点E在菱形ABCD的边BC的延长线上，AE交CD于点F，FG∥CE交DE于点G．求证：FG=FC．

查看试题解析
19.
如图，在△ABC中，已知AB=AC，D、E、B、C在同一条直线上，且AB²=BD•CE，求证：△ABD∽△ECA．

查看试题解析
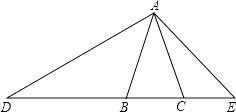20. 如图，已知AB是⊙O的直径，C是⊙O上的点，连接AC、CB，过O作EO∥CB并延长EO到F，使EO＝FO，连接AF并延长，AF与CB的延长线交于D.求证：AE²＝FG•FD.

查看试题解析
21. 如图，某学习小组为了测量校园内一棵小树的高度 $C D$ ，用长为 $1 m$ 的竹竿 $A B$ 作测量工具，移动竹竿，使竹竿影子的顶端、树影子的顶端落在水平地面上的同一点E，且点E，A，C在同一直线上.已知 $E A = 3 m$ ， $A C = 9 m$ ，求这棵树的高度 $C D$ .

查看试题解析
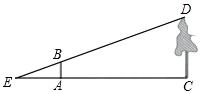22. 如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别是A（2，2）、B（4，0）、C（4，﹣4）．
①请画出△ABC向左平移6个单位长度后得到的△A₁B₁C₁；
②以点O为位似中心，将△ABC缩小为原来的 $\frac{1}{2}$ ，得到△A₂B₂C₂ ．

查看试题解析
23.
已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（0，3）、B（3，4）、C（2，2）（正方形网格中每个小正方形的边长是一个单位长度）．

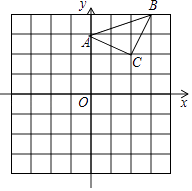(1)、画出△ABC向下平移4个单位长度得到的△A₁B₁C₁ ，

(2)、点C₁的坐标是；

(3)、以点B为位似中心，在网格内画出△A₂B₂C₂ ，

(4)、使△A₂B₂C₂与△ABC位似，且位似比为2：1，点C₂的坐标是．

查看试题解析

（人教版）2022-2023学年九年级数学下册第27章 相似 同步测试

一、单选题

二、填空题

三、解答题

（人教版）2022-2023学年九年级数学下册第27章相似同步测试