（人教版）2022-2023学年九年级数学下册27.3 位似 同步测试
试卷更新日期：2022-10-24 类型：同步测试
一、单选题
-
1. 如图，△ABC与ΔA′B′C′位似，位似中心为点O， ， △ABC的面积为9，则ΔA′B′C′面积为（ ）
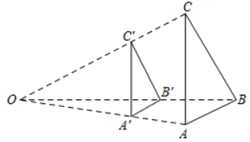A、 B、6 C、4 D、2. 如图，在平面直角坐标系中，△ABC与△A1B1C1是位似图形.其中BC∶B1C1=1∶2，则△ABC与△A1B1C1的周长之比是（ ）
A、1∶4 B、2∶1 C、1∶2 D、1∶33. 如图， 与 位似，点O为位似中心.已知 ， . 的周长为3，则 的周长是（ ）
A、4 B、6 C、9 D、274. 如图：△AOB与△A1OB1是以原点为位似中心的位似图形，且位似比为1：3，点B的坐标为（﹣1，2），则点B1的坐标为（ ）
A、（2，﹣4） B、（﹣2，4） C、（3，﹣6） D、（3，6）5. 如图，和是以点O为位似中心的位似图形，若 ， 则和的周长比为（ ）
A、 B、 C、 D、6. 如图，在坐标系xOy中，两个南开校徽图标是位似图形，位似中心是点O，①号校徽与②号校徽的位似比为2：1.点在②号校徽上，则在①号校徽上与点M对应的N点坐标为（ ）
A、 B、 C、 D、7. 如图，Rt△ABC中，∠ABC=90°，边AB在x轴上，以O为位似中心，作△A1B1C1与△ABC位似，若C（4，6）的对应点C1（2，3），则B1的坐标为（ ）
A、（1，0） B、（ ， 0） C、（2，0） D、（2，1）8. 如图，五边形ABCDE是由五边形FGHMN经过位似变换得到的，点O是位似中心，F、G、H、M、N分别是OA、OB、OC、OD、OE的中点，则五边形ABCDE与五边形FGHMN的面积比是（ ）
A、2：1 B、4：1 C、5：1 D、6：19. 如图，在直角坐标系中，△OAB的顶点为O(0，0)，A(4，3)，B(3，0).以点O为位似中心，在第三象限内作与△OAB的位似比为 的位似图形△OCD，则点C坐标（ ）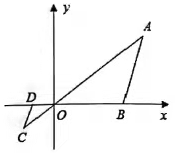
A、(- ，-1) B、(-1，- ) C、(-1，-1) D、(-2，-1)10. 如图，正方形ABCD和正方形EFOG是位似图形，其中点A与点E对应，点A的坐标为（-4，2）点E的坐标为（-1，1），则这两个正方形位似中心的坐标为（ ）
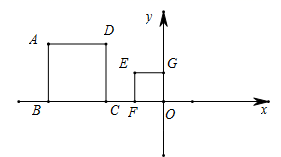A、(2，0) B、(1，1) C、（－2，0） D、（-1，0）二、填空题
-
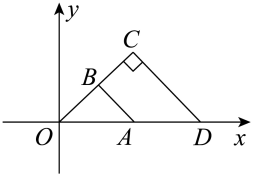
11. 如图，与是以点O为位似中心的位似图形，位似比为1∶2， ， ． 若 ， 则点C的坐标为 ．
12. 如图，四边形AEFH与四边形ABCD是位似图形，位似比为 ，且四边形ABCD的面积为900cm2 ， 则四边形AEFH的面积为cm2.
13. 在平面直角坐标系中，点 ， ，以原点O为位似中心，把 扩大为原来2倍，则点B的对应点 的坐标是.
14. 如图，在平面直角坐标系中，△ABC与△DEF关于原点O成位似关系，且相似比k＝ .若B（2，1），则点E的坐标是.
15. 如图，△ABC中，A、B两个顶点在x轴的上方，点C的坐标是（﹣1，0）．以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍．已知点B′的坐标是（3，﹣1），则点B的坐标是.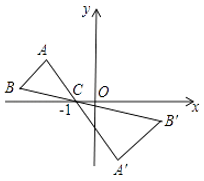
三、解答题
-
16. 如图，在平面直角坐标系中，△ABC三个顶点的坐标分别是A（2，2），B（4，0），C（4，﹣4）
①将△ABC绕点A顺时针旋转90°后得到△AB1C1 ， 在图①中画出△AB1C1 ， 并求出在旋转过程中△ABC
扫过的面积；
②在图②中以点O为位似中心，将△ABC缩小为原来的 ，并写出点C的对应点的坐标．
17.已知：△ABC在直角坐标平面内，三个顶点的坐标分别为A（1，0）、
B（3，2）、C（0，1）（正方形网格中每个小正方形的边长是一个单位长度）．
(1)、沿x轴向左平移2个单位，得到△A1B1C1 ， 不画图直接写出发生变化后的B1点的坐标．点B1的坐标是；(2)、①以A点为位似中心，在网格内画出△A2B2C2 ， 使△A2B2C2与△ABC位似，且位似比为2：1..②点B2的坐标是；
(3)、△A2B2C2的面积是平方单位．18. 如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点C的坐标为（4，﹣1）．
①以O为位似中心在第二象限作位似比为1：2变换，得到对应的△A1B1C1 ， 画出△A1B1C1 ， 并写出C1的坐标；
②以原点O为旋转中心，画出把△ABC顺时针旋转90°的图形△A2B2C2 ， 并写出C2的坐标．
19. 将图中的四边形作下列运动，画出相应的图形，并写出各个顶点的坐标；①关于y轴对称的四边形A′B′C′D′；
②以坐标原点O为位似中心，放大到原来的2倍的四边形A″B″C″D″．
20.如图，△ABC中，A、B两点在x轴的上方，点C的坐标是（﹣1，0）．以点C为位似中心，在x轴的下方作△ABC的位似图形△A′B′C，并把△ABC的边长放大到原来的2倍．设点B的对应点B′的横坐标是2，求点B的横坐标．
21. 在平面直角坐标系中，四边形OBCD与四边形OEFG位似，位似中心是原点O．已知C与F的坐标分别是C（3，7），F（9，21），那么四边形OBCD与四边形OEFG的相似比是多少？
