（人教版）2022-2023学年九年级数学下册27.2.2 相似三角形的性质同步测试

试卷更新日期：2022-10-24 类型：同步测试

进入出卷网下载

一、单选题

1. 如图，三个边长相等的正方形如图摆放，则 $∠ 1 + ∠ 2 + ∠ 3$ 的值为（）

A、 $60 °$ B、 $75 °$ C、 $90 °$ D、 $105 °$

查看试题解析
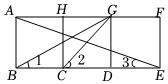2. 如图，在Rt△ABC中，∠ACB＝90°，CB＝7，AC＝9，以C为圆心、3为半径作⊙C，P为⊙C上一动点，连接AP、BP，则 $\frac{1}{3}$ AP+BP的最小值为（）

A、3 $\sqrt{2}$ . B、4 $\sqrt{3}$ C、3 $\sqrt{5}$ D、5 $\sqrt{2}$

查看试题解析
3. 已知 $△ A B C$ 的面积为16，点D，E分别为AB，AC边上的中点，则四边形DBCE的面积为（）

A、12 B、10 C、9 D、8

查看试题解析
4. 如图，△ABC中，E是AB的中点，过点E作ED∥BC，交AC于点D，则△AED与四边形BCDE的面积比是（）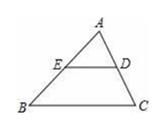

A、1：1 B、1：2 C、1：3 D、1：4

查看试题解析
5. 如图，正方形ABCD边长为2，BM，DN分别是正方形的两个外角的平分线，点P $Q$ 分别是平分线BM，DN上的点，且满足 $∠ P A Q = 45^{°}$ ，连接PQ，PC，CQ，则下列结论：①BP•DQ＝3.6②∠QAD＝∠APB，③∠PCQ＝135°④BP²+DQ²＝PQ² ，其中正确的有（）

A、4个 B、3个 C、2个 D、1个

查看试题解析
6. 如图，菱形ABCD的对角线AC，BD交于点P，且AC过原点O，AB∥x轴，点C的坐标为（6，3），反比例函数 $y = \frac{k}{x}$ 的图象经过A，P两点，则k的值是（）

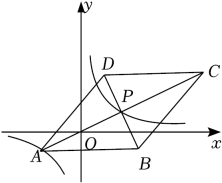A、4 B、3 C、2 D、1

查看试题解析
7. 如图，已知，DE∥BC， $\frac{A D}{D B} = \frac{1}{2}$ ，那么下列结论中，正确的是（　　）

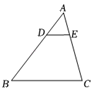A、 $\frac{D E}{B C} = \frac{1}{2}$ B、 $\frac{A E}{A C} = \frac{1}{3}$ C、 $\frac{A D}{A E} = \frac{1}{2}$ D、 $\frac{S_{△ A D E}}{S_{四边形 B D E C}} = \frac{1}{4}$

查看试题解析
8. 如图，菱形ABCD的边长为10，面积为80，∠BAD<90°，⊙O与边AB，AD都相切，菱形的顶点A到圆心O的距离为5，则⊙O的半径长等于（）

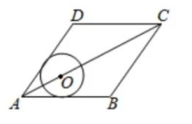A、2.5 B、 $\sqrt{5}$ C、2 $\sqrt{2}$ D、3

查看试题解析
9. 如图，点D是△ABC的边AB上的一点，过点D作BC的平行线交AC于点E，连接BE，过点D作BE的平行线交AC于点F，则下列结论不正确的是（）

A、 $\frac{A D}{B D} = \frac{A E}{E C}$ B、 $\frac{A F}{A E} = \frac{D F}{B E}$ C、 $\frac{A E}{E C} = \frac{A F}{F E}$ D、 $\frac{D E}{B C} = \frac{A F}{F E}$

查看试题解析
10. 如图，在4X6的正方形网格中，点A，B都在格点上，则 $\frac{B C}{A C}$ 的值是（）

A、 $\frac{2}{3}$ B、 $\frac{1}{2}$ C、 $\frac{2}{5}$ D、 $\frac{1}{3}$

查看试题解析

二、填空题

11. 如图， $△ A B C$ 和 $△ D E F$ 均为等腰三角形， $∠ A C B = ∠ D F E = 90 °$ ，点D为 $A B$ 的中点， $△ D E F$ 绕点D旋转，旋转过程中，线段 $D F$ 与线段 $A C$ 相交于点G，线段 $D E$ 与 $B C$ 的延长线相交于点H，若 $A B = 6 \sqrt{2}$ ， $A G = 2$ ，则 $C H$ 的长为．

查看试题解析
12. 如图，在菱形ABCD中，AB=6，∠DAB=60°，AE分别交BC、BD于点E、F，CE=2，连接CF，则tan∠DCF= ．

查看试题解析
13. 如图，⊙O的半径为5，点P在⊙O上，点A在⊙O内，且PA=3，过点A作AP的垂线交⊙O于点B，C.设PB= x ，PC=y，则y与x之间的函数解析式为

查看试题解析
14. 如图，在直角坐标系中，第一象限内的点A，B都在反比例函数 $y = \frac{k}{x}$ 的图象上，横坐标分别是3和1，点C在x轴的正半轴上，满足AC⊥BC．且BC＝2AC，则k的值是．

查看试题解析
15. 如图，在平面直角坐标系 $x O y$ 中，直线 $y = \frac{\sqrt{3}}{3} x + \frac{2 \sqrt{3}}{3}$ 与 $⊙ O$ 相交于A，B两点，且点A在x轴上，则弦 $A B$ 的长为.

查看试题解析

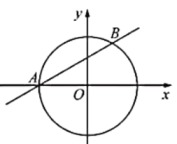
三、解答题

16. 如图，CD是⊙O的弦，AB是直径，CD⊥AB，垂足为P，求证：PC²＝PA·PB

查看试题解析
17. 如图，已知 $△ A B C ∽ △ A D E$ ，求证： $△ A B D ∽ △ A C E$ .

查看试题解析
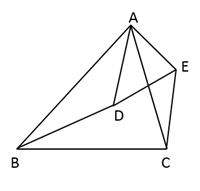18. 如图，在▱ABCD中，对角线AC，BD交于点O，过点O作EO⊥BD，交BA延长线于点E，交AD于点F，若EF=OF，∠CBD=30°，BD=6 $\sqrt{3}$ ．求AF的长．

查看试题解析
19. 如图，矩形DEFG的一边DE在△ABC的边BC上，顶点G、F分别在边AB、AC上，AH是边BC上的高，AH与GF相交于点K，已知BC=12，AH=6，EF∶GF=1∶2，求矩形DEFG的周长．

查看试题解析
20. 如图，点E，F分别为正方形ABCD边AB和CD上的中点， BE与AF交于点G.求证：AD²＝DG·DE

查看试题解析
21. 如图所示，该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在圆的半径的活动．小刚身高1.6米，测得其影长为2.4米，同时测得EG的长为3米，HF的长为1米，测得拱高（弧GH的中点到弦GH的距离，即MN的长）为2米，求小桥所在圆的半径．

查看试题解析
22. 如图，已知E为圆内两弦AB和CD的交点，直线EF∥CB，交AD的延长线于F，FG切圆于G．求证：EF=FG．

查看试题解析
23. 感知：如图①，在四边形ABCD中，AB∥CD，∠B=90°，点P在BC边上，当∠APD=90°时，可知△ABP∽△PCD．（不要求证明）
探究：如图②，在四边形ABCD中，点P在BC边上，当∠B=∠C=∠APD时，求证：△ABP∽△PCD．

拓展：如图③，在△ABC中，点P是边BC的中点，点D、E分别在边AB、AC上．若∠B=∠C=∠DPE=45°，BC=6 $\sqrt{2}$ ，CE=4，求DE的长

查看试题解析

（人教版）2022-2023学年九年级数学下册27.2.2 相似三角形的性质 同步测试

一、单选题

二、填空题

三、解答题

（人教版）2022-2023学年九年级数学下册27.2.2 相似三角形的性质同步测试