(人教版)2022-2023学年九年级数学下册27.2.1 相似三角形的判定 同步测试
试卷更新日期:2022-10-24 类型:同步测试
一、单选题
-
1. 如图,在△ABC中,DE∥AB,且= , 则的值为( )
 A、 B、 C、 D、2. 如图,直线, , 直线和被 , , 所截, , , , 则DE的长为( )
A、 B、 C、 D、2. 如图,直线, , 直线和被 , , 所截, , , , 则DE的长为( ) A、3 B、4 C、5 D、63. 如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )
A、3 B、4 C、5 D、63. 如图,正方形中,是的中点,是边上的一点,下列条件中,不能推出与相似的是( )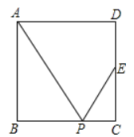 A、 B、 C、是的中点 D、4. 如图,中,是上一点,连接即并延长,交的延长线于点 , 则下列结论中正确的是( )
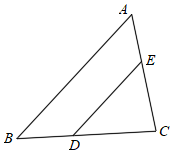
A、 B、 C、是的中点 D、4. 如图,中,是上一点,连接即并延长,交的延长线于点 , 则下列结论中正确的是( ) A、 B、 C、 D、5. 如图,△ABC中,若DE∥BC,EF∥AB,则下列比例式正确的是( )
A、 B、 C、 D、5. 如图,△ABC中,若DE∥BC,EF∥AB,则下列比例式正确的是( ) A、 B、 C、 D、6. 如图,下列不能判定 与 相似的是( )
A、 B、 C、 D、6. 如图,下列不能判定 与 相似的是( ) A、 B、 C、 D、7. 如图,直线l1∥l2∥l3 , 直线AC分别交l1 , l2 , l3于点A,B,C,直线DF分别交l1 , l2 , l3于点D,E,F.若 = ,则 的值为( )
A、 B、 C、 D、7. 如图,直线l1∥l2∥l3 , 直线AC分别交l1 , l2 , l3于点A,B,C,直线DF分别交l1 , l2 , l3于点D,E,F.若 = ,则 的值为( ) A、 B、 C、 D、8. 如图,在Rt△ABC中,∠CAB=90°,AD⊥CB,两两相似的三角形对数为( )
A、 B、 C、 D、8. 如图,在Rt△ABC中,∠CAB=90°,AD⊥CB,两两相似的三角形对数为( ) A、2 B、3 C、4 D、59. 如图,ΔABC的中线AD,BE交于点F,EG∥BC,交AD于点G,则 等于( )
A、2 B、3 C、4 D、59. 如图,ΔABC的中线AD,BE交于点F,EG∥BC,交AD于点G,则 等于( ) A、1:2 B、1:3 C、2:3 D、3:510. 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC~△AED的是( )
A、1:2 B、1:3 C、2:3 D、3:510. 如图,在△ABC中,点D、E分别在边AB、AC上,下列条件中不能判断△ABC~△AED的是( )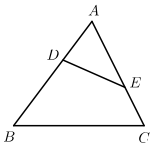 A、∠AED=∠B B、∠ADE=∠C C、 D、
A、∠AED=∠B B、∠ADE=∠C C、 D、二、填空题
-
11. 如图,已知 , 如果 , , 则的长是.
 12. 如图,正方形ABCD的顶点D在反比例函数(x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,若△BCE的面积是6,则k的值为.
12. 如图,正方形ABCD的顶点D在反比例函数(x<0)的图象上,顶点B,C在x轴上,对角线AC的延长线交y轴于点E,连接BE,若△BCE的面积是6,则k的值为. 13. 如图,在平面直角坐标系中,双曲线 ( )与直线 ( )交于A、B两点,点H是双曲线第一象限上的动点(在点A左侧),直线AH、BH分别与y轴交于P、Q两点,若 , ,则a-b的值为.
13. 如图,在平面直角坐标系中,双曲线 ( )与直线 ( )交于A、B两点,点H是双曲线第一象限上的动点(在点A左侧),直线AH、BH分别与y轴交于P、Q两点,若 , ,则a-b的值为. 14. 如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为.
14. 如图,△ABC中,D、F在AB边上,E、G在AC边上,DE∥FG∥BC,且AD:DF:FB=3:2:1,若AG=15,则EC的长为. 15. 下列命题:①函数中,函数y随x的增大而减小,②有一个角相等的两个等腰三角形相似,③两个等边三角形相似,④平分弦的直径垂直于弦,⑤相等的圆周角所对的弧相等,⑥关于x的函数的图象是抛物线.其中正确的结论有(填序号).
15. 下列命题:①函数中,函数y随x的增大而减小,②有一个角相等的两个等腰三角形相似,③两个等边三角形相似,④平分弦的直径垂直于弦,⑤相等的圆周角所对的弧相等,⑥关于x的函数的图象是抛物线.其中正确的结论有(填序号).三、解答题
-
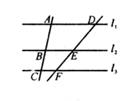
16. 如图,直线l1∥l2∥l3 , 直线AC依次交l1 , l2 , l3于A,B,C三点,直线DF依次交l1 , l2 , l3于D,E,F三点,若 ,DE=12,求EF的长.
 17. 如图,在△ABC和OACD中,AD⊥CD于点D,AC⊥BC于点C.请再添加一个条件,使△ABC∽△CAD,并加以证明.
17. 如图,在△ABC和OACD中,AD⊥CD于点D,AC⊥BC于点C.请再添加一个条件,使△ABC∽△CAD,并加以证明. 18. 如图,弦BC经过圆心D,AD⊥BC,AC交⊙D于E,AD交 ⊙D于M,BE交AD于N.求证:△BND∽△ABD.
18. 如图,弦BC经过圆心D,AD⊥BC,AC交⊙D于E,AD交 ⊙D于M,BE交AD于N.求证:△BND∽△ABD. 19.
19.如图,点C、D在线段AB上,△PCD是等边三角形,若∠APB=120°,求证:△ACP∽△PDB.
 20. 如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= CD.求证:△ABF∽△CEB.
20. 如图,平行四边形ABCD中,E是CD的延长线上一点,BE与AD交于点F,DE= CD.求证:△ABF∽△CEB.