（人教版）2022-2023学年九年级数学下册26.2实际问题与反比例函数同步测试

试卷更新日期：2022-10-24 类型：同步测试

进入出卷网下载

一、单选题

1. 购买 $x$ 斤水果需 $24$ 元，购买一斤水果的单价 $y$ 与 $x$ 的关系式是（）

A、 $y = \frac{24}{x} (x > 0)$ B、 $y = \frac{24}{x}$ （ $x$ 为自然数） C、 $y = \frac{24}{x}$ （ $x$ 为整数） D、 $y = \frac{24}{x}$ （ $x$ 为正整数）

查看试题解析
2. 小明学习了物理中的杠杆平衡原理发现：阻力 $\times$ 阻力臂 $=$ 动力 $\times$ 动力臂．现已知某一杠杆的阻力和阻力臂分别为2400N和1m，则动力 $F$ （单位：N）关于动力臂 $l$ （单位：m）的函数图象大致是（）

A、 B、 C、 D、

查看试题解析
3. 验光师测得一组关于近视眼镜的度数y（度）与镜片焦距x（米）的对应数据如下表.根据表中数据，可得y关于x的函数表达式为
近视眼镜的度数y（度）
200
250
400
500
1000
镜片焦距x（米）
0.50
0.40
0.25
0.20
0.10

A、 $y = \frac{100}{x}$ B、 $y = \frac{x}{100}$ C、 $y = \frac{400}{x}$ D、 $y = \frac{x}{400}$

查看试题解析
4. 三角形的面积S为定值，一条底边为y，这底边上的高为x，则y关于x的函数图象大致上是（）

A、 B、 C、 D、

查看试题解析
5.
如图，已知直线y=﹣x+4与两坐标轴分别相交于点A，B两点，点C是线段AB上任意一点，过C分别作CD⊥x轴于点D，CE⊥y轴于点E．双曲线 $y = \frac{k}{x}$ 与CD，CE分别交于点P，Q两点，若四边形ODCE为正方形，且 $S_{△ O P Q} = \frac{3}{2}$ ，则k的值是（）

A、4 B、2 C、 $\frac{3}{2}$ D、 $\frac{5}{3}$

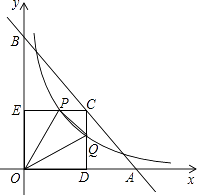查看试题解析
6. 下列关系式中，y是x反比例函数的是（　　）

A、y= $\frac{1}{2 x}$ B、y= $\frac{5}{x}$ -1 C、y=- $\frac{1}{x^{2}}$ D、y= $\frac{2}{x + 1}$

查看试题解析
7. 下列函数中，图象经过点（1，﹣1）的反比例函数解析式是（　　）

A、y= $\frac{1}{x}$ B、y= $\frac{- 1}{x}$ C、y= $\frac{2}{x}$ D、y= $\frac{- 2}{x}$

查看试题解析
8. 已知反比例函数的图象经过点P（1，﹣2），则这个函数的图象位于（　　）

A、第一、三象限 B、第二、三象限 C、第二、四象限 D、第三、四象限

查看试题解析
9. 如果反比例函数y= $\frac{k}{x}$ 的图象经过点（﹣2，﹣3），那么k的值为（　　）

A、 $\frac{3}{2}$ B、 $\frac{2}{3}$ C、-6 D、6

查看试题解析
10. 已知正比例函数y=2x与反比例函数y= $\frac{2}{x}$ 的图象相交于A，B两点，若A点的坐标为（1，2），则B点的坐标为（　　）

A、（1，﹣2） B、（﹣1，2） C、（﹣1，﹣2） D、（2，1）

查看试题解析

二、填空题

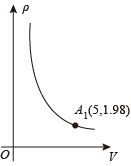
11. 密闭容器内有一定质量的二氧化碳，在温度不变的情况下，当容器的体积V（单位：m³）变化时，气体的密度ρ（单位：kg/m³）随之变化，已知密度ρ是体积V的反比例函数关系，它的图象如图所示，则当ρ = 3.3 kg/m³时，相应的体积V是 m³.

查看试题解析
12. 某物体对地面的压强p（Pa）与物体和地面的接触面积S（m²）成反比例函数关系（如图）。当该物体与地面的接触面积为0.25m²时，该物体对地面的压强是 Pa。

查看试题解析
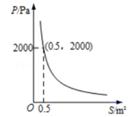13. 某户家庭用购电卡购买了2 000度电，若此户家庭平均每天的用电量为x(单位：度)，这2 000度电能够使用的天数为y(单位：天)，则y与x的函数关系式为y＝.

查看试题解析
14. 计划修建水渠1000米，则修建天数y和每日修建量x之间的函数关系式为．

查看试题解析
15. 我们学习过反比例函数．例如，当矩形面积S一定时，长a是宽b的反比例函数，其函数关系式可以写为a= $\frac{s}{b}$ （S为常数，S≠0）．请你仿照上例另举一个在日常生活、生产或学习中具有反比例函数关系的量的实例，并写出它的函数关系式．实例：；函数关系式：．

查看试题解析

三、解答题

16. 张华同学在一次做电学实验时，记录下电流I（安）与电阻R（欧）有如表对应关系：
R
…
2
4
8
10
16
…
I
…
16
8
4
3.2
2
…
通过描点连线，观察并求出I与R之间的函数关系式．

查看试题解析
17. 一个面积为42的长方形，其相邻两边长分别为x和y，请你写出与之间的函数解析式，并画出其图象．

查看试题解析
18. 某电器商场销售甲、乙两种品牌空调，已知每台乙种品牌空调的进价比每台甲种品牌空调的进价高20％，用7200元购进的乙种品牌空调数量比用3000元购进的甲种品牌空调数量多2台．

(1)、求甲、乙两种品牌空调的进货价；

(2)、该商场拟用不超过16000元购进甲、乙两种品牌空调共10台进行销售，其中甲种品牌空调的售价为2500元／台，乙种品牌空调的售价为3500元／台．请您帮该商场设计一种进货方案，使得在售完这10台空调后获利最大，并求出最大利润．

查看试题解析
19. 面积一定的梯形，其上底长是下底长的 $\frac{1}{3}$ ，设上底长为xcm，高为ycm，且当x=5cm，y=6cm，

(1)、求y与x的函数关系式；

(2)、求当y=4cm时，下底长多少？

查看试题解析
20. 某三角形的面积为15cm² ，它的一边长为xcm，且此边上高为ycm，请写出x与y之间的关系式，并求出x=5时，y的值．

查看试题解析
21. 甲、乙两地相距100km，一辆汽车从甲地开往乙地，把汽车到达乙地所用的时间t（h）表示为汽车速度v（km/h）的函数，并说明t是v的什么函数．

查看试题解析
22. 一个圆锥的体积是100cm³ ，求底面积S（cm²）与高h（cm）之间的函数关系式及自变量的取值范围．

查看试题解析
23.
如图，E为矩形ABCD的边CD上的一个动点，BF⊥AE于F，AB=2，BC=4，设AE=x，BF=y，求y与x之间的关系式，并写出x的取值范围．

查看试题解析

近视眼镜的度数y（度）	200	250	400	500	1000
镜片焦距x（米）	0.50	0.40	0.25	0.20	0.10

R	…	2	4	8	10	16	…
I	…	16	8	4	3.2	2	…