浙江省台州市2022-2023学年八年级上学期第一次月考（10月）数学试题
试卷更新日期：2022-10-24 类型：月考试卷
一、单选题(共30分)
-
1. 第24届冬季奥林匹克运动会于2022年2月20日在世界首个“双奥之城”——北京圆满落下帷幕．下列图中所示的四个图案是四届冬季奥林匹克运动会会徽图案上的一部分图形，其中是轴对称图形的是（ ）A、
B、
C、
D、
2. 根据下列已知条件，能画出唯一的△ABC的是（ ）A、AB=5，BC=4，AC=10 B、∠A=45°，∠C=60°，BC=8 C、∠A=80°，AB=6，BC=7 D、∠C=90°，AB=93. 下列说法正确的是（ ）A、如果两个三角形全等，则它们必是关于某条直线成轴对称的图形 B、如果两个三角形关于某条直线成轴对称，那么它们是全等三角形 C、等腰三角形是关于一条边上的中线成轴对称的图形 D、一条线段是关于经过该线段中点的直线成轴对称图形4. 已知△ABC的三个内角度数之比为3∶4∶5，则此三角形是（ ）三角形．A、锐角 B、钝角 C、直角 D、不能确定5. 如图，AD是△ABC 的角平分线，DF⊥AB，垂足为F，且DE＝DG，则∠AED＋∠AGD和是（ ）
A、180° B、200° C、210° D、240°6. 如图所示，已知∠AOB＝60°，点P在边OA上，OP＝10，点M，N在边OB上，PM＝PN，若MN＝2，则OM的长为（ ）
A、3 B、4 C、5 D、67. 如图1，已知 AB=AC，D为∠BAC 的平分线上一点，连接 BD、 CD；如图2，已知 AB= AC，D、E为∠BAC的平分线上两点，连接 BD，CD，BE，CE；如图3，已知 AB=AC，D，E，F为∠BAC的平分线上三点，连接BD，CD，BE，CE， BF，CF；…，依次规律，第 n个图形中全等三角形的对数是（ ）
A、n B、2n-1 C、 D、3（n+1）8. 如图，AB＝AC，点D、E分别在AC、AB上，且AE＝AD，连接EC，BD，EC交BD于点M，连接AM，过点A分别作AF⊥CE，AG⊥BD，垂足分别为F、G，则下列结论错误的是（ ）
A、△EBM≌△DCM B、若S△BEM＝S△ADM，则E是AB的中点 C、MA平分∠EMD D、若E是AB的中点，则BM+AC＜EM+BD9. 如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，过点O作EFBC交AB于E，交AC于F，过点O作OD⊥AC于D．下列四个结论：①∠BOC＝90°∠A，②∠EBO∠AEF，③∠DOC+∠OCB＝90°，④设OD＝m，AE+AF＝n，则S△AEF ． 其中正确的结论有（ ）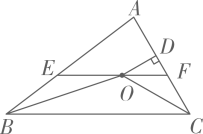
A、1个 B、2个 C、3个 D、4个10. 如图，在等边△ABC中，BF是AC边上的中线，点D在BF上，连接AD，在AD的右侧作等边△ADE，连接EF，当△AEF周长最小时，∠CFE的大小是（ ）
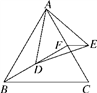A、30° B、45° C、60° D、90°二、填空题(共24分)
-
11. 已知点A（x ， ﹣4）与点B（3，y）关于x轴对称，那么x+y的值为 ．12. 如图，则∠A+∠B+∠C+∠D+∠E的度数是.
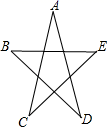13. 如图，△ ADB≌△ ECB，且点A的对应点是点E，点D的对应点是点C，若∠ CBD＝40°，BD⊥ EC，则∠ D的度数为 ．
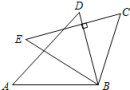14. 如图是5×5的正方形网格，△ABC的顶点都在小正方形的顶点上，像△ABC这样的三角形叫格点三角形，画与△ABC有一条公共边且全等的格点三角形，这样的格点三角形最多可以画个.
15. 如图，点E是等边△ABC内一点，且EA＝EB，△ABC外一点D满足BD＝AC，且BE平分∠DBC，则∠D＝.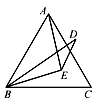
16. 如图，在 ABC中，AH是高，AE BC，AB＝AE，在AB边上取点D，连接DE，DE＝AC，若 ，BH＝1，则BC＝.
三、解答题(共66分)
-
17. 如图，在中，是边上的一点， ， 平分 ， 交边于点 ， 连接 ． 求证：；
18. 如图，已知△ABC≌△DEF，点B，E，C，F在同一直线上．
(1)、若∠BED＝130°，∠D＝70°，求∠ACB的度数；(2)、若2BE＝EC，EC＝6，求BF的长．19. 如图，已知AD是△ABC的边BC上的高，点E为AD上一点，且BE=AC，DE=DC．
(1)、证明：∠DBE=∠DAC；(2)、若AE=4，CD=2，求△ABC的面积20. 如图，平面直角坐标系中，A（﹣2，1），B（﹣3，4），C（﹣1，3），过点（1，0）作x轴的垂线l．
(1)、作出△ABC关于直线l的轴对称图形；(2)、直接写出（ ， ），（ ， ），（ ， ）；(3)、在△ABC内有一点P（m，n），则点P关于直线l的对称点的坐标为（ ， ）（结果用含m，n的式子表示）．21. 如图，直线是中BC边的垂直平分线，点P是直线m上的一动点，若 ， ， ．
(1)、求的最小值，并说明理由．(2)、求周长的最小值．22. 如图①，∠1、∠2是四边形ABCD的两个不相邻的外角．
(1)、猜想并说明∠1+∠2与∠A、∠C的数量关系；(2)、如图②，在四边形ABCD中，∠ABC与∠ADC的平分线交于点O．若∠A＝58°，∠C＝152°，求∠BOD的度数；(3)、如图③，BO、DO分别是四边形ABCD外角∠CBE、∠CDF的角平分线．请直接写出∠A、∠C与∠O的数量关系．
