浙江省绍兴市柯桥区2022-2023学年八年级上学期月考数学试卷(10月)
试卷更新日期:2022-10-24 类型:月考试卷
一、选择题(每小题2分,共20分)
-
1. 下列图案中,是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 以下列各组线段为边,能组成三角形的是( )A、2,3,4 B、5,5,11 C、1,2,3 D、3,7,43. 对于命题“如果∠1+∠2=90°,那么∠1=∠2”,能说明它是假命题的反例是( )A、∠1=45°,∠2=45° B、∠1=50°,∠2=50° C、∠1=50°,∠2=40° D、∠1=40°,∠2=40°4. 在数学课上,同学们在练习画边AC上的高时,有一部分同学画出下列四种图形,请你判断一下,正确的是( )A、
2. 以下列各组线段为边,能组成三角形的是( )A、2,3,4 B、5,5,11 C、1,2,3 D、3,7,43. 对于命题“如果∠1+∠2=90°,那么∠1=∠2”,能说明它是假命题的反例是( )A、∠1=45°,∠2=45° B、∠1=50°,∠2=50° C、∠1=50°,∠2=40° D、∠1=40°,∠2=40°4. 在数学课上,同学们在练习画边AC上的高时,有一部分同学画出下列四种图形,请你判断一下,正确的是( )A、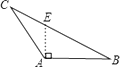 B、
B、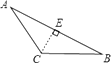 C、
C、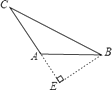 D、
D、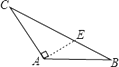 5. 如图,在四边形ABCD中,∠ACB=∠DAC,添加一个条件后不能保证△BAC≌△DCA的是( )
5. 如图,在四边形ABCD中,∠ACB=∠DAC,添加一个条件后不能保证△BAC≌△DCA的是( )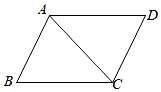 A、AB∥CD B、∠B=∠D C、AB=CD D、AD=BC6. 如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( )
A、AB∥CD B、∠B=∠D C、AB=CD D、AD=BC6. 如图是一个平分角的仪器,其中AB=AD,BC=DC,将点A放在角的顶点,AB和AD沿着角的两边放下,沿AC画一条射线,这条射线就是角的平分线,在这个操作过程中,运用了三角形全等的判定方法是( )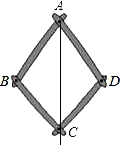 A、SSS B、SAS C、ASA D、AAS7. 如图,在△ABC中,D、E、F分别为BC、AD、CE的中点,且S△ABC=12cm2 , 则阴影部分△AEF的面积为( )cm2 .
A、SSS B、SAS C、ASA D、AAS7. 如图,在△ABC中,D、E、F分别为BC、AD、CE的中点,且S△ABC=12cm2 , 则阴影部分△AEF的面积为( )cm2 .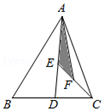 A、1 B、1.5 C、2 D、38. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )
A、1 B、1.5 C、2 D、38. 如图,把△ABC纸片沿DE折叠,当点A落在四边形BCDE内部时,则∠A与∠1+∠2之间有一种数量关系始终保持不变,请试着找一找这个规律,这个规律是( )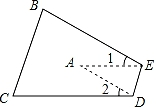 A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)9. 如图,在△ABC中,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是( )
A、∠A=∠1+∠2 B、2∠A=∠1+∠2 C、3∠A=2∠1+∠2 D、3∠A=2(∠1+∠2)9. 如图,在△ABC中,AB=3,AC=4,BC=5,EF垂直平分BC,点P为直线EF上的任一点,则AP+BP的最小值是( )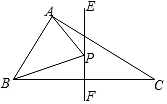 A、7 B、6 C、5 D、410. 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1 , 得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2 , 得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3 , 得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=( )
A、7 B、6 C、5 D、410. 如图,∠BOC=9°,点A在OB上,且OA=1,按下列要求画图:以A为圆心,1为半径向右画弧交OC于点A1 , 得第1条线段AA1;再以A1为圆心,1为半径向右画弧交OB于点A2 , 得第2条线段A1A2;再以A2为圆心,1为半径向右画弧交OC于点A3 , 得第3条线段A2A3…这样画下去,直到得第n条线段,之后就不能再画出符合要求的线段了,则n=( )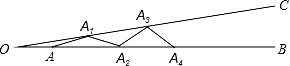 A、10 B、9 C、8 D、7
A、10 B、9 C、8 D、7二、填空题(每小题3分,共30分)
-
11. 命题:面积相等的两个三角形是全等三角形是命题(填“真”或“假”)12. 已知一个等腰三角形两边分别为4和6,那么这个等腰三角形的周长为 .
13.工人师傅在做完门框后,为防止变形常常像图中所示的那样上两条斜拉的木条(即图中的AB,CD两根木条),这样做的依据是 .
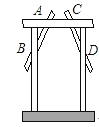 14. 如图,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是.
14. 如图,已知AC=BD,要使△ABC≌△DCB,只需增加的一个条件是. 15. 将一副三角板如图所示摆放(其中一块三角板的一条直角边与另一块三角板的斜边摆放在一直线上),那么图中∠α=度.
15. 将一副三角板如图所示摆放(其中一块三角板的一条直角边与另一块三角板的斜边摆放在一直线上),那么图中∠α=度.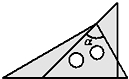 16. 等腰三角形一腰上的高与另一边的夹角为40°,则这个等腰三角形顶角的度数为 .17. 如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长是cm.
16. 等腰三角形一腰上的高与另一边的夹角为40°,则这个等腰三角形顶角的度数为 .17. 如图,在△ABC中,DE是AC的垂直平分线,AE=3cm,△ABD的周长为13cm,则△ABC的周长是cm.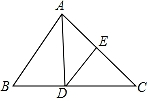 18. 如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则S△ABO:S△BCO:S△CAO等于 .
18. 如图,△ABC的三边AB、BC、CA长分别是20、30、40,其三条角平分线将△ABC分成三个三角形,则S△ABO:S△BCO:S△CAO等于 .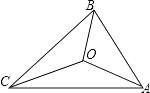 19. 如图,AD是△ABC的中线,E是AD上一点,BE交AC于F.若BE=AC,BF=9,CF=6,则AF的长度为 .
19. 如图,AD是△ABC的中线,E是AD上一点,BE交AC于F.若BE=AC,BF=9,CF=6,则AF的长度为 .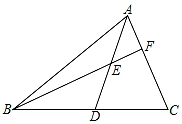 20. 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有 .
20. 如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ,OC,以下五个结论:①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP;⑤OC平分∠AOE.一定成立的结论有 .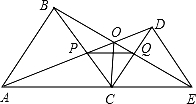
三、解答题(共50分)
-
21. 如图,AB∥CD , AB=CD , 点E , F在BC上,且BE=CF .
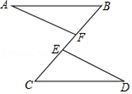
求证:
(1)、AF=DE;
(2)、AF∥DE .
22. 两个村庄M,N与两条公路AC,AB的位置如图所示,现打算在O处建一个垃圾回收站,要求回收站到两个村庄M,N的距离必须相等,到两条公路AC,AB的距离也必须相等,那么点O应选在何处?请在图中用尺规作图中找出点O.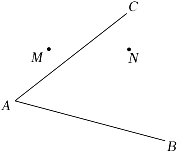 23. 如图,在△ABD和△ACE中,有下列四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.请你以其中三个等式作为题设,余下的作为结论,写出一个正确的结论(要求写出已知,求证及证明过程)
23. 如图,在△ABD和△ACE中,有下列四个等式:①AB=AC;②AD=AE;③∠1=∠2;④BD=CE.请你以其中三个等式作为题设,余下的作为结论,写出一个正确的结论(要求写出已知,求证及证明过程)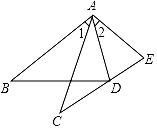 24. 如图,在△ABC中,AD是BC边上的高线,AE平分∠BAC,若∠BAC:∠B:∠C=4:3:2,求∠DAE的度数.
24. 如图,在△ABC中,AD是BC边上的高线,AE平分∠BAC,若∠BAC:∠B:∠C=4:3:2,求∠DAE的度数.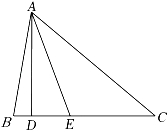 25. 如图,△ABC的∠ABC和∠ACB的平分线BD,CE相交于点F,∠A=60°,
25. 如图,△ABC的∠ABC和∠ACB的平分线BD,CE相交于点F,∠A=60°,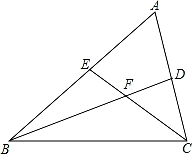 (1)、求∠BFC的度数.(2)、求证:BC=BE+CD.26. 如图,△ABC与△ADE都是等边三角形(三条边都相等,三个内角都相等的三角形),连接BD、CE交点记为点F.
(1)、求∠BFC的度数.(2)、求证:BC=BE+CD.26. 如图,△ABC与△ADE都是等边三角形(三条边都相等,三个内角都相等的三角形),连接BD、CE交点记为点F.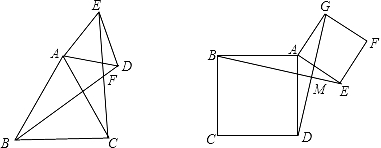 (1)、BD与CE相等吗?请说明理由.(2)、你能求出BD与CE的夹角∠BFC的度数吗?(3)、若将已知条件改为:四边形ABCD与四边形AEFG都是正方形,连接BE、DG,交点记为点M(如图).请直接写出线段BE和DG之间的关系?27. 如图,已知在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.
(1)、BD与CE相等吗?请说明理由.(2)、你能求出BD与CE的夹角∠BFC的度数吗?(3)、若将已知条件改为:四边形ABCD与四边形AEFG都是正方形,连接BE、DG,交点记为点M(如图).请直接写出线段BE和DG之间的关系?27. 如图,已知在△ABC中,AB=AC=10厘米,BC=8厘米,点D为AB的中点.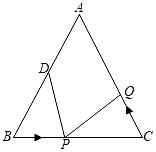 (1)、如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.
(1)、如果点P在线段BC上以3厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.①若点Q的运动速度与点P的运动速度相等,则经过1秒后,△BPD与△CQP是否全等?请说明理由;
②若点Q的运动速度与点P的运动速度不相等,则当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)、若点Q以②中的运动速度从C点出发,点P以原来的运动速度从B点同时出发,都逆时针沿△ABC的三边运动,求经过多长时间点P与点Q第一次在△ABC的哪条边上相遇.