陕西省延安市富县2021-2022学年八年级上学期期中数学试题
试卷更新日期：2022-10-24 类型：期中考试
一、单选题
-
1. 剪纸是我国传统的民间艺术，下列剪纸作品中，是轴对称图形的是（ ）A、
B、
C、
D、
2. 下列四组线段，不能组成三角形的是（ ）A、2cm，3cm，3cm B、3cm，3cm，3cm C、2cm，6cm，5cm D、5cm，6cm，l3cm3. 在平面直角坐标系中，若点M（2，m）和N（2，5）关于x轴对称，则m的值为（ ）A、﹣5 B、﹣2 C、2 D、54. 如图，在△ABC中，EF垂直平分AC ， 分别交AB ， AC于点D ， F ， 交CB的延长线于点E ． 若BD＝3cm，CD＝9cm，则AB的长为（ ）
A、14cm B、12cm C、10cm D、9cm5. 如图，在四边形ABCD中，∠A＝90°，AD＝4cm，BC＝7cm，对角线BD平分∠ABC ， 则△BCD的面积为（ ）
A、16cm2 B、15cm2 C、12.5cm2 D、14cm26. 将正六边形与正五边形按如图所示方式摆放，公共顶点为O，且正六边形的边AB与正五边形的边DE在同一条直线上，则∠COF的度数是（ ）
A、74° B、76° C、84° D、86°7. 如图，已知△ABC≌△DEC ， 点A和点D ， 点B和点E是对应顶点，过点A作AF⊥CD交CD于点F ， 若∠BCE＝60°，则∠CAF的度数为（ ）
A、35° B、30° C、60° D、65°8. 如图，在△ABC中，∠BAC＝90°，AD是高，BE是中线，CF是角平分线，CF交AD于点G ， 交BE于点H ， 以下结论：①S△ABE＝S△BCE；②∠AFG＝∠AGF；③∠FAG＝2∠ACF；④AF＝FB ． 其中正确结论的个数有（ ）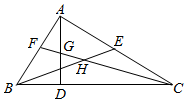
A、4个 B、3个 C、2个 D、1个二、填空题
-
9. 如图所示，要使一个六边形木架在同一平面内不变形，至少还要再钉上 根木条．
10. 如图，BC∥EF ， BC＝EF ， 请你添加一个条件：使得△ABC≌△DEF ． （写出一个即可）
11. 如图，在△ABC中，点D ， E分别在边AB ， BC上，点A与点E关于直线CD对称．若AB＝8cm，AC＝10cm，BC＝14cm，则△DBE的周长为 ．
12. 如图，在△ABC中，交AC于点E ， 交BC于点F ， 连接DC ． 若∠A＝70°，∠D＝38°，则∠DCA的度数是 ．
13. 如图，在△AOB和△COD中，OA＝OB ， OC＝OD（OA＜OC），∠AOB＝∠COD＝α ， 直线AC ， BD交于点M ， 连接OM ． 以下结论：①AC＝BD；②∠OAM＝∠OBM；③∠AMB＝α；④OM平分∠BOC ． 其中正确的是 ． （填序号）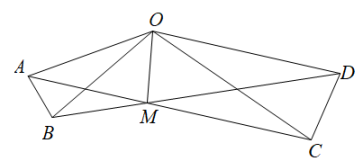
三、解答题
-
14. 在△ABC中，已知∠B＝∠A+10°，∠C＝∠B+25°，求∠A的度数．15. 如图，在△ABC中，∠C＝90°，BD平分∠ABC，交AC于点D．若CD＝2，E为AB上一动点，求出DE的最小值．
16. 如图，在平面直角坐标系中，已知点A（1，2），B（3，1），C（﹣2，﹣1）．在图中作出△ABC关于y轴对称的△A1B1C1 ， 并写出点C1的坐标．
17. 已知一个多边形的每个外角都是其相邻内角度数的 ， 求这个多边形的边数．18. 如图，已知OA和OB是两条公路，C ， D是两个村庄，建立一个车站M ， 使车站到两个村庄距离相等，即MC＝MD ， 且M到OA ， OB两条公路的距离相等．请用尺规作图法作出点M的位置．（保留作图痕迹，不写作法）
19. 已知三角形三边长分别为a ， b ， c ， 其中a ， b满足（a﹣8）2+|b﹣6|＝0，求这个三角形的第三边长c的取值范围．20. 如图，点B ， E ， C ， F在一条直线上，AB＝DE ， AC＝DF ， BF＝CE ． 试说明：AB∥DE ．
21. 如图，AD平分∠BAC ， DE⊥AB于点E ， DF⊥AC于点F ．求证：AD垂直平分EF ．
22. 如图，已知四边形ABCD与四边形EFGH关于直线MN对称，∠D＝130°，∠A+∠B＝155°，AD＝4cm，EF＝5cm．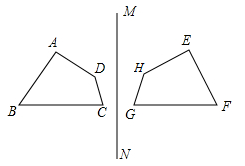
(1)、求出AB ， EH的长度以及∠G的度数；(2)、连接AE ， DH ， AE与DH平行吗？为什么？23. 在的正方形格点图中，有格点和 ， 且和关于某直线成轴对称，请在备用图中画出4个这样的 ．
24. 如图②，是小朋友荡秋千的侧面示意图，静止时秋千位于铅垂线BD上，转轴B到地面的距离BD＝2.5m．乐乐在荡秋千过程中，当秋千摆动到最高点A时，测得点A到BD的距离AC＝1.5m，点A到地面的距离AE＝1.5m，当他从A处摆动到A'处时，若A'B⊥AB，求A'到BD的距离．
25. 如图，在△ABC中，∠ACB＝60°，D为△ABC边AC上一点，BC＝CD ， 点M在BC的延长线上，CE平分∠ACM ， 且AC＝CE ． 连接BE交AC于点F ， G为边CE上一点，满足CG＝CF ， 连接DG交BE于点H ．
(1)、求∠DHF的度数；(2)、若EB平分∠DEC ， 则BE平分∠ABC吗？请说明理由．26. 如图1，在长方形ABCD中，AB＝CD＝8cm，BC＝12cm，点M从点B出发，以2cm/s的速度沿BC向点C运动，设点M的运动时间为ts．
(1)、MC＝cm；（用含t的代数式表示）(2)、若△ABM≌△DCM ， 求出此时t的值；(3)、如图2，当点M从点B开始运动时，点N同时从点C出发，以xcm/s的速度沿CD向点D运动，是否存在这样的x值，使得△ABM与△MNC全等？若存在，请求出x的值；若不存在，请说明理由．