陕西省西安市莲湖区2021-2022学年八年级上学期期中数学试题
试卷更新日期：2022-10-24 类型：期中考试
一、单选题
-
1. 以下点在第二象限的是（ ）A、（0，0） B、（3，﹣5） C、（﹣1，9） D、（﹣2，﹣1）2. 若式子在实数范围内有意义，则x的取值范围是（ ）A、x≥3 B、x≤3 C、x＞3 D、x＜33. 在实数 ， π， ， ， ﹣1.626626662……中，无理数的个数是（ ）A、1个 B、2个 C、3个 D、4个4. 下列根式中最简二次根式的是（）A、 B、 C、 D、5. 下列四组数中，是勾股数的是（）A、5，12，13 B、 ， ， C、1， ， D、7，24，266. 一等腰三角形，腰长10cm，底长16cm，则底边上的高是（ ）A、8cm B、6cm C、10cm D、12cm7. 已知实数x ， y满足＋（y﹣3）2＝0，则经过点（x ， y）的直线表达式可能是（ ）A、y＝x＋4 B、y＝x﹣4 C、y＝2x＋1 D、y＝2x﹣28. 正比例函数y＝kx（k≠0）的图像经过第一、三象限，则一次函数y＝x﹣k的图像大致是（ ）A、
B、
C、
D、
二、填空题
-
9. 比较大小：﹣﹣2．（填“＞”、“＝”或“＜”）10. 点A（x1 ， y1）（x2 ， y2）是一次函数y＝﹣2x＋b图像上的两个点，且x1＞x2 ， 则y1与y2的大小关系是 ．11. 一次函数y＝﹣2x＋b向上平移3个单位后经过（2，0），则b＝ ．12. 如图，点A表示的数为3，过点A作AB⊥OA于点A ， 且AB＝2，以O为圆心，OB长为半径作弧，弧与数轴的交点C表示的数是 ．
13. 已知点M（2，5），N（0，1），点P在x轴上，且PM＋PN最短，则P的坐标是 ．三、解答题
-
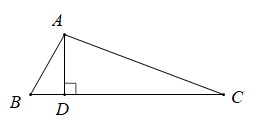
14. 计算： ．15. 计算： ．16. 已知点A（m﹣2，5）和B（3，n＋4），A ， B两点关于y轴对称，求m﹣n的值．17. 已知一个正数x的两个平方根分别为a＋1和a﹣5，求x﹣1的立方根．18. 已知点（m＋1，2m﹣3）到两坐标距离相等，求m的值．19. 如图，在树干的顶部A和地面B、C两点处引两条绳子AB ， AC ， 已知树干AD的长为12m，BD的长为5m，DC的长为16m，AD⊥BC ， 求绳子总长．
20. 某汽车在加油后开始匀速行驶．已知汽车行驶到20km时，油箱中剩油53L，行驶到50km时，油箱中剩油50L ， 如果油箱中剩余油量y（1）与汽车行驶路程x（km）之间是一次函数关系，请求出这个一次函数表达式，并写出自变量的取值范围．21. 做4个全等的直角三角形，设它们的两条直角边分别为a ， b ， 斜边为c ， 再做一个边长为c的正方形，把它们按如图的方式拼成正方形，请用这个图证明勾股定理．
22. 如图，圆柱形容器高为0.8m，底面周长为4.8m在容器内壁离底部0.1m的点B处有一只蚊子，此时一只壁虎正好在容器的顶部点A处，则壁虎扑捉蚊子的最短路程是多少？
23. 已知一次函数y＝﹣3x＋6，完成下列问题．
(1)、在如下的平面直角坐标系中画出函数图象并求出与x轴的交点坐标．(2)、根据图像回答：当x时，y＞324. 如图△ABC在正方形网格中，网格每一小格长度为1，若A（﹣1，4）．按要求回答下列问题．
(1)、在图中建立平面直角坐标系，并写出B和C的坐标；(2)、计算△ABC的面积．25. 如图，在平面直角坐标系中，直线l1：y＝kx﹣1与y轴交于点B ， 与x轴交于点C ， 直线l2：y＝x＋1与y轴交于点D ． 直线l1和直线l2相交于点A ， 已知A点纵坐标为2
(1)、求点A的横坐标及k的值．(2)、点M在直线l2上，MN∥y轴，交x轴于点N ， 若MN＝2BD ， 求点M的坐标．26. 阅读材料研究平面直角坐标系，我们可以发现一条重要的规律：若平面直角坐标系上有两个不同的点A（xA ， yA）、B（xB ， yB），则线段AB的中点坐标可以表示为（ ， ）．
(1)、问题提出如图1，直线AB与y轴交于点A（0，4），与x轴交于点B（6，0），过原点O的直线L将△ABO分成面积相等的两部分，请求出直线L的解析式．
(2)、问题解决同学通过观察发现“若四边形一条对角线平分四边形的面积，则这条对角线必经过另一条对角线的中点”，如图2，在四边形ABCD中，对角线AC、BD相交于点O ， 若S△ABD＝S△BCD ， 则可得AO＝CO ． 根据上述结论，在如图3的平面直角坐标系中，M（1，6），N（4，﹣3），C（5m ， m＋2），若OC恰好平分四边形OMCN的面积，求点C的坐标．