2022年秋季湘教版数学九年级上册第五章 《用样本推断总体》单元检测A
试卷更新日期：2022-10-21 类型：单元试卷
一、单选题（每题3分，共30分）
-
1. 若一组数据1，2，4，3， ， 0的平均数是2，则众数是（ ）A、1 B、2 C、3 D、42. 某学习小组做摸球试验，在一个不透明的袋子里装有红、黄两种颜色的小球共20个，除颜色外都相同．将球搅匀后，随机摸出5个球，发现3个是红球，估计袋中红球的个数是（ ）A、12 B、9 C、8 D、63. 一组数据：3，4，4，6，若添加一个数据6，则不发生变化的统计量是（ ）A、平均数 B、中位数 C、众数 D、方差4. 甲、乙、丙、丁四人进行射击测试，每人10次射击的平均成绩恰好都是9.2环，方差分别是s甲2＝0.12，s乙2＝0.59，s丙2＝0.33，s丁2＝0.46，在本次射击测试中，这四个人成绩最稳定的是（ ）A、甲 B、乙 C、丙 D、丁5. 下列说法正确的是（ ）A、对角线相等的四边形是矩形. B、相似三角形的面积的比等于相似比. C、方差越大，数据的波动越大；方差越小，数据的波动越小. D、过一点有且只有一条直线与已知直线平行.6. 希望中学规定学生的学期体育成绩满分为100，其中体育课外活动占20%，期中考试成绩占30%，期末考试成绩占50%.若小强的三项成绩（百分制）依次是95，90，91.则小强这学期的体育成绩是（ ）A、92 B、91.5 C、91 D、907. 垃圾分类利国利民，某校宣传小组就“空矿泉水瓶应投放到哪种颜色的垃圾收集桶内”进行统计活动，他们随机采访50名学生并作好记录．以下是排乱的统计步骤：
①从扇形统计图中分析出本校学生对空矿泉水瓶投放的正确率；
②整理采访记录并绘制空矿泉水瓶投放频数分布表；
③绘制扇形统计图来表示空矿泉水瓶投放各收集桶所占的百分比.
正确统计步骤的顺序应该是（ ）A、②→③→① B、②→①→③ C、③→①→② D、③→②→①8. 第1组数据为：0、0、0、1、1、1，第2组数据为：、 ， 其中、是正整数．下列结论：①当时，两组数据的平均数相等；②当时，第1组数据的平均数小于第2组数据的平均数；③当时，第1组数据的中位数小于第2组数据的中位数；④当时，第2组数据的方差小于第1组数据的方差．其中正确的是（ ）A、①② B、①③ C、①④ D、③④9. “俭以养德”是中华民族的优秀传统，时代中学为了对全校学生零花钱的使用进行符合题意引导，随机抽取50名学生，对他们一周的零花钱数额进行了统计，并根据调查结果绘制了不完整的频数分布表和扇形统计图，如图所示：组别
零花钱数额/元
频数
一
二
12
三
15
四
五
5
关于这次调查，下列说法正确的是（ ）
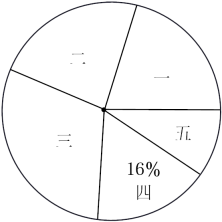A、总体为50名学生一周的零花钱数额 B、五组对应扇形的圆心角度数为36° C、在这次调查中，四组的频数为6 D、若该校共有学生1500人，则估计该校零花钱数额不超过20元的人数约为1200人10. 某中学青年志愿者协会的10名志愿者，一周的社区志愿服务时间如下表所示：时间/h
2
3
4
5
6
人数
1
3
2
3
1
关于志愿者服务时间的描述正确的是（ ）
A、众数是6 B、平均数是4 C、中位数是3 D、方差是1二、填空题（每题3分，共18分）
-
11. 在甲、乙两位射击运动员的10次考核成绩中，两人的考核成绩的平均数相同， 方差分别为 ， ， 则考核成绩更为稳定的运动员是（填“甲”、“乙”中的一个）12. 学校要从王静，李玉两同学中选拔一人参加运动会志愿者工作，选拔项目为普通话，体育知识和旅游知识.并将成绩依次按4∶3∶3计分. 两人的各项选拔成绩如右表所示，则最终胜出的同学是.
普通话
体育知识
旅游知识
王静
80
90
70
李玉
90
80
70
13. 今年4月23日是第27个世界读书日，某校举行了演讲大赛，演讲得分按“演讲内容”占40%、“语言表达”占40%、“形象风度”占10%、“整体效果”占10%进行计算，小芳这四项的得分依次为85，88，92，90，则她的最后得分是分.14. 某射击运动队进行了五次射击测试，甲、乙两名选手的测试成绩如图所示，甲、乙两选手成绩的方差分别记为 ， 则.（填“>”“<”或“=”）
15. 为落实立德树人，发展素质教育，加强美育，需要招聘两位艺术老师，从学历、笔试、上课和现场答辩四个项目进行测试，以最终得分择优录取，甲、乙、丙三位应聘者的测试成绩（10分制）如表所示，如果四项得分按照“1：1：1：1”比例确定每人的最终得分，丙得分最高，甲与乙得分相同，分不出谁将被淘汰；鉴于教师行业应在“上课“项目上权重大一些（其他项目比例相同），为此设计了新的计分比例，你认为三位应聘者中（填：甲、乙或丙）将被淘汰.成绩
应聘者
甲
乙
丙
学历
9
8
9
笔试
8
7
9
上课
7
8
8
现场答辩
8
9
8
16. 为了比较甲、乙两鱼池中的鱼苗数目，小明从两鱼池中各捞出100条鱼苗，每条做好记号，然后放回原鱼池；一段时间后，在同样的地方，小明再从甲、乙两鱼池中各捞出100条鱼苗，发现其中有记号的鱼苗分别是5条、10条，可以初步估计鱼苗数目较多的是 鱼池（填甲或乙）三、解答题（共8题，共72分）
-
17. 目前，全球淡水资源分布不均、总量不足是人类面临的共同问题，某市在实施居民用水定额管理前，通过简单随机抽样对居民生活用水情况进行了调查，获得了若干个家庭去年的月均用水量数据（单位：t），整理出了频数分布表，频数分布直方图和扇形统计图，部分信息如下：
月均用水量（t）
2≤x＜3.5
3.5≤x＜5
5≤x＜6.5
6.5≤x＜8
8≤x＜9.5
频数
7
6
对应的扇形区域
A
B
C
D
E
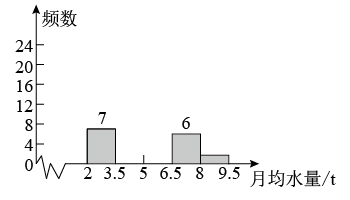
根据以上信息，解答下列问题：
(1)、补全频数分布直方图，并求出扇形图中扇形E对应的圆心角的度数；(2)、为了鼓励节约用水，要确定一个用水量的标准，超出这个标准的部分按1.5倍价格收费，若要使该市60％的家庭水费支出不受影响，你觉得家庭月均用水量应该定为多少？并说明理由．18. 某公司要在甲、乙两人中招聘一名职员，对两人的学历、能力、经验这三项进行了测试，各项满分均为10分，成绩高者被录用．图1是甲、乙测试成绩的条形统计图．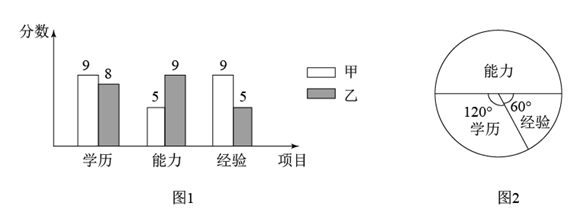
(1)、分别求出甲、乙三项成绩之和，并指出会录用谁；(2)、若将甲、乙的三项测试成绩，按照扇形统计图（图2）各项所占之比，分别计算两人各自的综合成绩，并判断是否会改变（1）的录用结果．19. 人口问题是“国之大者”．以习近平同志为核心的党中央高度重视人口问题，准确把握人口发展形势，有利于推动社会持续健康发展，为开启全面建设社会主义现代化国家新征程、向第二个百年奋斗目标进军创造良好的条件．某综合与实践研究小组根据我国第七次人口普查数据进行整理、描述和分析，给出部分数据信息：信息一：普查登记的全国大陆31个省、自治区、直辖市人口数的频数分布直方图如下：
（数据分成6组： ， ， ， ， ， ）
信息二：普查登记的全国大陆31个省、自治区、直辖市人口数（百万人）在 这一组的数据是：58，47，45，40，43，42，50；
信息三：2010——2021年全国大陆人口数及自然增长率；
请根据以上信息，解答下列问题：
(1)、普查登记的全国大陆31个省、自治区、直辖市人口数的中位数为百万人．(2)、下列结论正确的是 ． （只填序号）①全国大陆31个省、自治区、直辖市中人口数大于等于100（百万人）的有2个地区；
②相对于2020年，2021年全国大陆人口自然增长率降低，全国大陆人口增长缓慢；
③2010-2021年全国大陆人口自然增长率持续降低．
(3)、请写出2016-2021年全国大陆人口数、全国大陆人口自然增长率的变化趋势，结合变化趋势谈谈自己的看法．20. 合理的膳食可以保证青少年体格和智力的正常发育．综合实践小组为了解某校学生膳食营养状况，从该校1380名学生中调查了100名学生的膳食情况，调查数据整理如下：
中国营养学会推荐的三大营养素供能比参考值
蛋白质
10%~15%
脂肪
20%~30%
碳水化合物
50%~65%
注：供能比为某物质提供的能量占人体所需总能量的百分比．
(1)、本次调查采用的调查方法；（填“普查”或“抽样调查”）(2)、通过对调查数据的计算，样本中的蛋白质平均供能比约为14.6%，请计算样本中的脂肪平均供能比和碳水化合物平均供能比；(3)、结合以上的调查和计算，对照下表中的参考值，请你针对该校学生膳食状况存在的问题提一条建议．21. 某校举办“歌唱祖国”演唱比赛，十位评委对每位同学的演唱进行现场打分，对参加比赛的甲、乙、丙三位同学得分的数据进行整理、描述和分析，下面给出了部分信息．a．甲、乙两位同学得分的折线图：
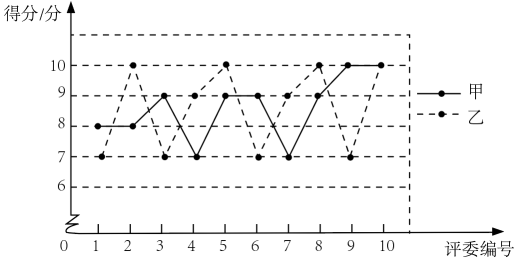
b．丙同学得分：
10，10，10，9，9，8，3，9，8，10
c．甲、乙、丙三位同学得分的平均数：
同学
甲
乙
丙
平均数
8.6
8.6
m
根据以上信息，回答下列问题：
(1)、求表中m的值；(2)、在参加比赛的同学中，如果某同学得分的10个数据的方差越小，则认为评委对该同学演唱的评价越一致．据此推断：甲、乙两位同学中，评委对的评价更一致（填“甲”或“乙”）；(3)、如果每位同学的最后得分为去掉十位评委打分中的一个最高分和一个最低分后的平均分，最后得分越高，则认为该同学表现越优秀．据此推断：在甲、乙、丙三位同学中，表现最优秀的是（填“甲”“乙”或“丙”）。22. 综合与实践【问题情境】数学活动课上，老师带领同学们开展“利用树叶的特征对树木进行分类”的实践活动，
【实践发现】同学们随机收集芒果树、荔枝树的树叶各10片，通过测量得到这些树叶的长y（单位：cm），宽x（单位：cm）的数据后，分别计算长宽比，整理数据如下：
1
2
3
4
5
6
7
8
9
10
芒果树叶的长宽比
3.8
3.7
3.5
3.4
3.8
4.0
3.6
4.0
3.6
4.0
荔枝树叶的长宽比
2.0
2.0
2.0
2.4
1.8
1.9
1.8
2.0
1.3
1.9
【实践探究】分析数据如下：
平均数
中位数
众数
方差
芒果树叶的长宽比
3.74
m
4.0
0.0424
荔枝树叶的长宽比
1.91
1.95
n
0.0669
【问题解决】
(1)、上述表格中， ， ；(2)、①A同学说：“从树叶的长宽比的方差来看，我认为芒果树叶的形状差别大.”②B同学说：“从树叶的长宽比的平均数、中位数和众数来看，我发现荔枝树叶的长约为宽的两倍.”
上面两位同学的说法中，合理的是（填序号）
(3)、现有一片长 ，宽 的树叶，请判断这片树叶更可能来自于芒果、荔枝中的哪种树?并给出你的理由.23. 电视剧《一代洪商》在中央电视台第八套播出后，怀化市各旅游景点知名度得到显菩提高.为全面提高旅游服务质量，旅游管理部门随机抽取了100名游客进行满意度调查，并绘制成如下不完整的频数分布表和扇形统计图.频数分布表
满意程度
频数（人）
频率
非常满意
50
0.5
满意
30
0.3
一般
a
c
不满意
b
0.05
合计
100
1
根据统计图表提供的信息，解答下列问题：
(1)、a＝ ， b＝ ， c＝；(2)、求扇形统计图中表示“一般”的扇形圆心角α的度数；(3)、根据调查情况，请你对各景点的服务提一至两条合理建议.24. 某校为响应“传承屈原文化·弘扬屈原精神”主题阅读倡议，进一步深化全民阅读和书香宜昌建设，随机抽取了八年级若干名学生，对“双减”后学生周末课外阅读时间进行了调查.根据收集到的数据，整理后得到下列不完整的图表：时间段/分钟
组中值
75
105
135
频数/人
6
20
4
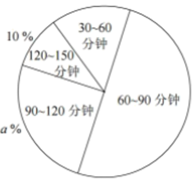
请你根据图表中提供的信息，解答下面的问题：
(1)、扇形统计图中，120~150分钟时间段对应扇形的圆心角的度数是； ；样本数据的中位数位于~分钟时间段；(2)、请将表格补充完整；(3)、请通过计算估计该校八年级学生周末课外平均阅读时间.